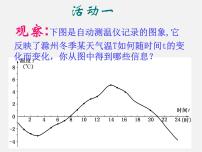
初中数学沪科版八年级上册第13章 三角形中的边角关系、命题与证明13.2 命题与证明评课课件ppt

这是一份初中数学沪科版八年级上册第13章 三角形中的边角关系、命题与证明13.2 命题与证明评课课件ppt，共15页。PPT课件主要包含了回顾与思考，提高训练，试说明等内容，欢迎下载使用。

1、什么叫做命题2、命题的类型3、命题的结构（命题的组成部分）4、命题的一般形式5、什么样的两个命题叫做互逆命题6、什么样的命题只可举出反例就行
7、什么叫做定义8、什么叫做公理9、什么叫做定理10、什么叫做证明（演绎推理）11、证明真命题的一般步骤
1.如何证明三角形内角和等于180°？ 理解将三角形内角和转化为“平角”的 化归思想。2.什么是辅助线？ 添加辅助线应注意的事项？3.掌握三角形内角和定理的推论1.
三角形的内角和等于180°
∵ ∠2=∠B∴ CE∥BA ∴∠B=∠2 又∵∠1+∠2+∠ACB=180° ∴∠A+∠B+∠ACB=180°
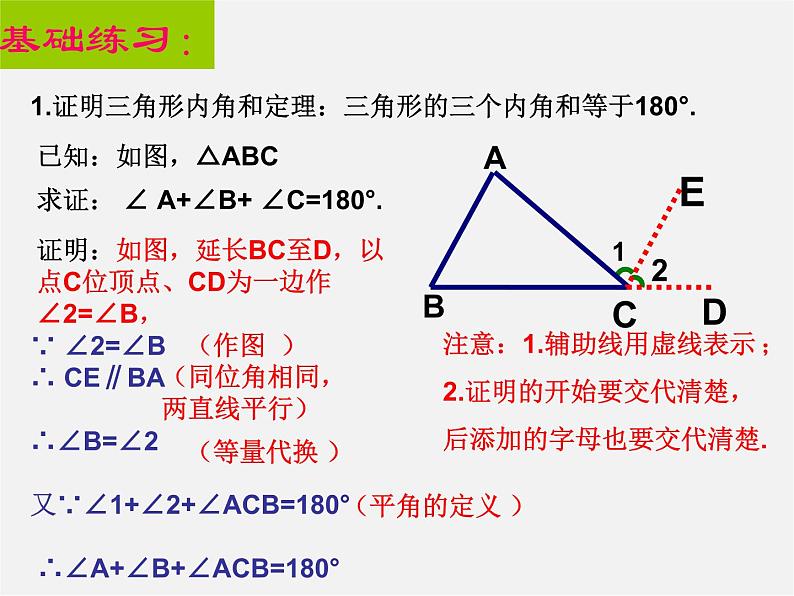
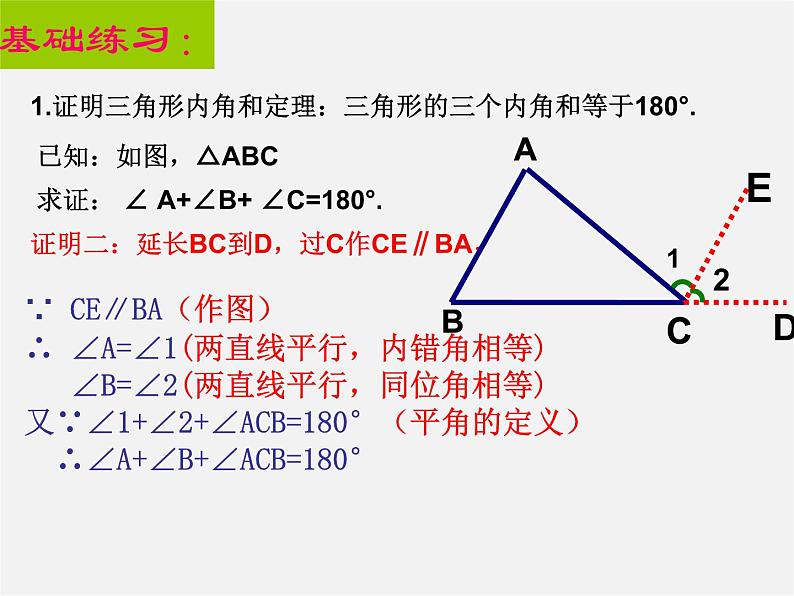
1.证明三角形内角和定理：三角形的三个内角和等于180°.
求证： ∠ A+∠B+ ∠C=180°.
注意：1.辅助线用虚线表示；2.证明的开始要交代清楚，后添加的字母也要交代清楚.
证明：如图，延长BC至D，以点C位顶点、CD为一边作∠2=∠B，
（同位角相同， 两直线平行）
证明二：延长BC到D，过C作CE∥BA，
∵ CE∥BA（作图）∴ ∠A=∠1(两直线平行，内错角相等) ∠B=∠2(两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180°（平角的定义） ∴∠A+∠B+∠ACB=180°
证法3：过A作EF∥BA，
∵ EF∥BA（作图）∴∠B=∠2(两直线平行,内错角相等) ∠C=∠1(两直线平行,内错角相等) 又 ∵∠2+∠1+∠BAC=180°（平角的定义） ∴∠B+∠C+∠BAC=180°
开启 智慧
你还有其他方法来证明三角形内角和定理吗？
添加辅助线思路：1、构造平角 2、构造同旁内角
三角形内角和定理 三角形三个内角的和等于1800.△ABC中,∠A+∠B+∠C=1800.
三角形内角和定理的几种变形:∠A=1800 –(∠B+∠C).∠B=1800 –(∠A+∠C).∠C=1800 –(∠A+∠B).∠A+∠B=1800-∠C.∠B+∠C=1800-∠A.∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
辅助线是为了证明需要在原图上添画的线.（辅助线通常画成虚线）它的作用是把分散的条件集中，把隐含的条件显现出来，起到牵线搭桥的作用.添加辅助线，可构造新图形，形成新关系，找到联系已知与未知的桥梁，把问题转化，但辅助线的添法没有一定的规律，要根据需要而定,平时做题时要注意总结.
1..直角三角形的两锐角具有什么关系？
直角三角形的两锐角互余
有两个角互余的三角形是直角三角形
下面的正六边形，你能根据自己的知识求出六边形的内角和吗？
4个三角形：180°×4＝720°
六角螺母的面是六边形，它的内角都相等，则这个六边形的每个内角是 　　　　 。
本节课学习了什么内容？