数学八年级下册9.4 矩形、菱形、正方形背景图课件ppt

这是一份数学八年级下册9.4 矩形、菱形、正方形背景图课件ppt，共22页。PPT课件主要包含了菱形的性质，想一想，菱形的识别，又∵ABAD，菱形的判定，AC⊥BD，又∵AB5，∴AC⊥BD，∴∠AOB90°，请你动脑筋等内容，欢迎下载使用。

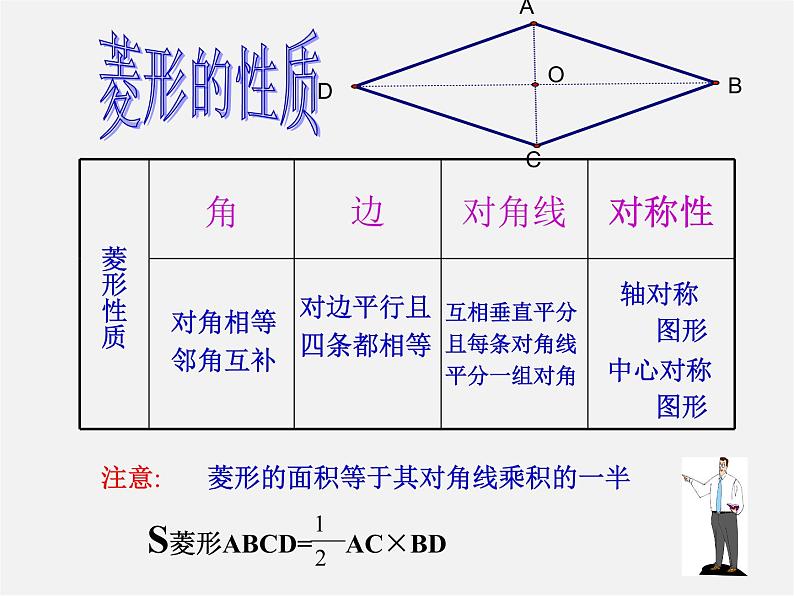
互相垂直平分且每条对角线平分一组对角
轴对称 图形 中心对称 图形
注意: 菱形的面积等于其对角线乘积的一半
如果一个四边形是平行四边形，则只要再有什么条件就可以判定它是一个菱形？根据什么？
有一组邻边相等的平行四边形叫做菱形.
平行四边形再加上一个什么条件 是菱形呢?
由菱形的定义我们得到识别菱形的一条途径:
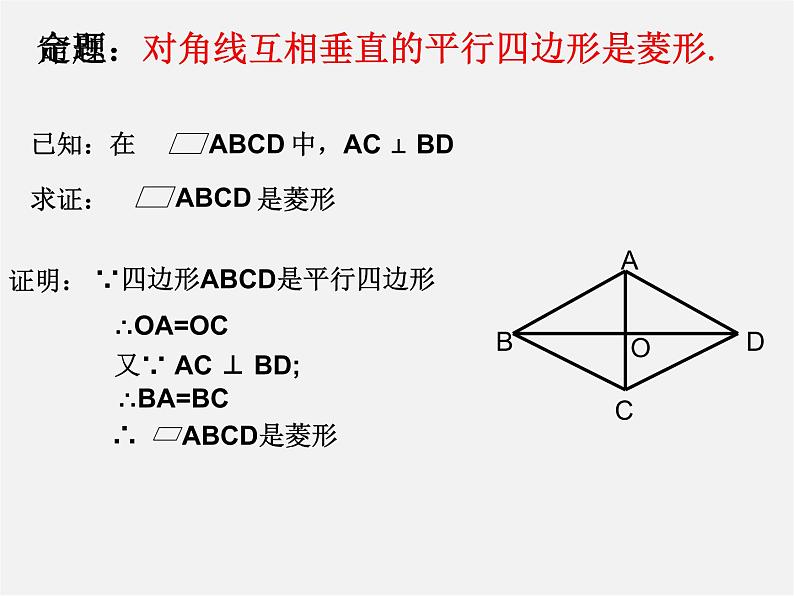
命题：对角线互相垂直的平行四边形是菱形.
∴ ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
定理：对角线互相垂直的平行四边形是菱形.
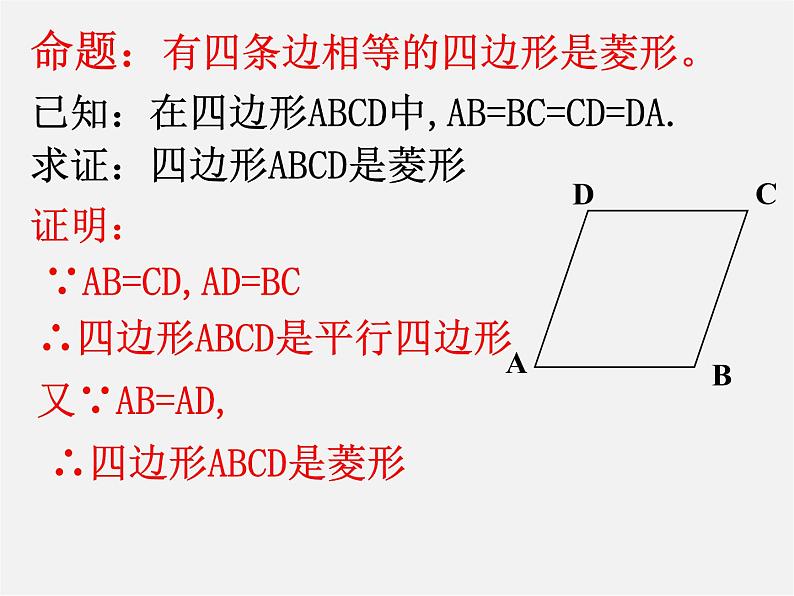
命题：有四条边相等的四边形是菱形。
已知：在四边形ABCD中,AB=BC=CD=DA.求证：四边形ABCD是菱形
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
∴四边形ABCD是菱形
∵AB=BC=CD=DA
一组邻边相等的平行四边形是菱形
四边形加上一个什么条件是菱形呢?
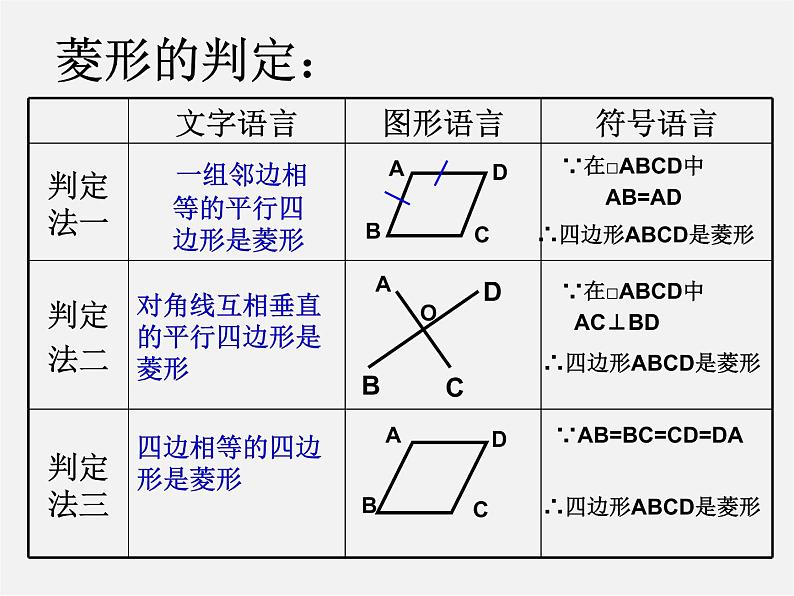
定义：一组邻边相等的平行四边形是菱形
判定定理：四条边都相等的四边形是菱形
判定定理：对角线互相垂直的平行四边形是菱形
AD=DC=CB=BA
老师说下列三个图形都是菱形,你相信吗?
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
例1、已知：如图，AD平分∠BAC，DE∥AC 交AB于E，DF∥AB交AC于F． 求证：四边形AEDF是菱形．
证明：∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC∴∠2=∠3
∵ AD是△ABC的角平分线∴ ∠1=∠2
∴四边形ABCD是菱形.
∴OA=OC=4 OB=OD=3
又∵ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
∴AB2=AO2+BO2
例3、如图，ΔAOD，ΔAOB， ΔCOB， ΔCOD是四个彼此全等的直角三角形。四边形ABCD是菱形吗？
例4、已知：如图,□ ABCD的对角线AC的垂直平分线与边AD，BC分别交于E，F．求证：四边形AFCE是菱形
∴AO=CO, ∠AOE=90°
∴∠FOC=∠AOE=90°
∴ AD∥BC ∴AE∥FC
∴四边形AFCE是平行四边形
∴四边形AFCE是菱形
练习1：□ABCD的对角线AC与BD相交于点O， （1）若AB=AD，则□ABCD是 形； （2）若AC=BD，则□ABCD是 形； （3）若∠ABC是直角，则□ABCD是 形； （4）若∠BAO=∠DAO，则□ABCD是 形。
2、判断下列说法是否正确？为什么？(1)对角线互相垂直的四边形是菱形； （ ）(2)对角线互相垂直平分的四边形是菱形；（ ）(3)对角线互相垂直,且有一组邻边相等 的四边形是菱形； （ ）(4)两条邻边相等，且一条对角线平分一 组对角的四边形是菱形． （ ）
（1）.下列命题中正确的是（ ） A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形 C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
（2）.对角线互相垂直且平分的四边形是（ ） A.矩形 B.一般的平行四边形 C.菱形 D.以上都不对
（3）.下列条件中，不能判定四边形ABCD为菱形的是（ ） A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
把两张等宽的纸条交叉重叠在一起，你能判断重叠部分ABCD的形状吗？