四川省德阳广汉市2021-2022学年八年级上学期期中考试数学试题（word版 含答案）

2021-2022学年度上期期中考试试卷

八年级数学

考试范围：第11、12章、14.1整式的乘法；考试时间：120分钟；满分：150分

第Ⅰ卷（选择题）

一、选择题（本大题共12个小题，每小题4分，共48分）在每小题给出的四个选项中，有且仅有一项是符合题目要求的．

1．以下列各组线段为边，能组成三角形的是（　　）

A．2cm，3cm，5cm B．3cm，3cm，6cm  

C．2cm，5cm，8cm D．4cm，5cm，6cm

2．下列运算正确的是（　　）

A．（a+1）2=a2+1  B．3ab2c÷a2b=3ab 

C．（﹣2ab2）3=8a3b6 D．x3·x=x4

3．用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）

A                 B               C              D

4．如图，AB＝DB，BC＝BE，欲证△ABE≌△DBC，则可增加的条件是（　　）

A．∠ABE＝∠DBE 

B．∠A＝∠D 

C．∠E＝∠C 

D．∠1＝∠2

5．如图，如果△ABC≌△FED，那么下列结论错误的是（　　）

A．EC＝BD B．EF∥AB 

C．DF＝BD D．AC∥FD

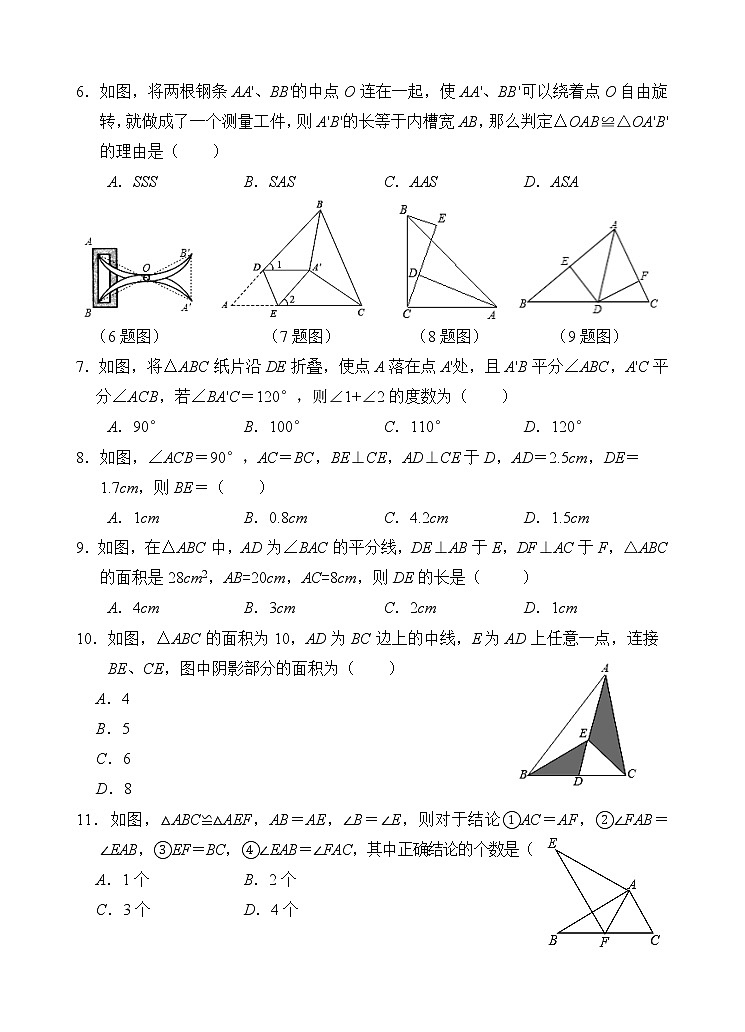
6．如图，将两根钢条AA'、BB'的中点O连在一起，使AA'、BB'可以绕着点O自由旋转，就做成了一个测量工件，则A'B'的长等于内槽宽AB，那么判定△OAB≌△OA'B'的理由是（　　）

A．SSS B．SAS C．AAS D．ASA

（6题图）            （7题图）         （8题图）        （9题图）

7．如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝120°，则∠1+∠2的度数为（　　）

A．90° B．100° C．110° D．120°

8．如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D，AD＝2.5cm，DE＝1.7cm，则BE＝（　　）

A．1cm B．0.8cm C．4.2cm D．1.5cm

9．如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是28cm2，AB=20cm，AC=8cm，则DE的长是（　 　）

A．4cm B．3cm C．2cm D．1cm

10．如图，△ABC的面积为10，AD为BC边上的中线，E为AD上任意一点，连接BE、CE，图中阴影部分的面积为（　　）

A．4 

B．5 

C．6 

D．8

11．如图，△ABC≌△AEF，AB＝AE，∠B＝∠E，则对于结论①AC＝AF，②∠FAB＝∠EAB，③EF＝BC，④∠EAB＝∠FAC，其中正确结论的个数是（　　）

A．1个 B．2个 

C．3个 D．4个

12．如图，在四边形ABCD中，AD∥BC．若∠DAB的角平分线AE交CD于E，连接BE，且BE边平分∠ABC，得到如下结论：①∠AEB＝90°；②BC+AD＝AB；③BE＝CD；④BC＝CE；⑤若AB＝x，则BE的取值范围为0＜BE＜x，那么以上结论正确的是（    ）

A．①②③ B．②③④ 

C．①④⑤ D．①②⑤．

第Ⅱ卷（非选择题）

二、填空题（本大题共6个小题，每小题4分，共24分，将答案填在答题卡对应的题号后的横线上）

13．计算：22018×0.52018＝　   　．

14．（4a2－8a）÷2a＝　   　．

15．如图，已知BD＝CE，∠B＝∠C，若AB＝8，AD＝3，则DC＝　 　  ．

（15题图）              （16题图）                    （17题图）

16．如图，△ABC中，点A的坐标为（0，1），点C的坐标为（4，3），如果要使△ABD与△ABC全等，那么点D的坐标是　                　．

17．如图，小明从A点出发前进10m，向右转20°，再前进10m，又向右转20°，…，这样一直走下去，他第一次回到出发点A时，一共走了　    　m．

18．已知方格纸中的每个小方格是边长为1的正方形，A，B两点在小方格的顶点上，位置如图所示，在小方格的顶点上确定一点C，连接AB，AC，BC，使△ABC的面积为3个平方单位．则这样的点C共有　  　个．

三、解答题（本大题共7小题，共78分．答应写出文字说明、证明过程或推演步骤）

19．(10分)

（1）先化简，再求值：，其中a＝4．

（2）若a，b，c分别为三角形的三边，化简：|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|

20．（10分）如图，已知点B，E，C，F在一条直线上，BE＝CF，AC∥DE，∠A＝∠D．

（1）求证：△ABC≌△DFE；

（2）若BF＝14，EC＝4，求BC的长．

21．（10分）两个大小不同的等腰直角三角形三角板，如图①所示放置，图②是由它抽象出的几何图形，点B，C，E在同一条直线上，连接DC．

（1）请找出图②中的全等三角形，并给予证明．（说明：结论中不得含有未标识的字母）

（2）证明：DC⊥BE．

22．（10分）如图，在△ABC中，∠BAC=120°，AD，BE分别为△ABC的角平分线，连结DE．

（1）求证：点E到DA，DC的距离相等；

（2）求∠DEB的度数．

23．（12分）如图1所示，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，直线MN经过点A，BD⊥MN于点D，CE⊥MN于点E．

（1）求证：∠ABD＝∠CAE；

（2）求证：DE＝BD+CE；

（3）当直线MN运动到如图2所示位置时，其余条件不变，直接写出线段DE、BD、CE之间的数量关系．

24．（12分）在△ABC中，AB＝AC，D是直线BC上一点，以AD为一条边在AD的右侧作△ADE，使AE＝AD，∠DAE＝∠BAC，连接CE．

（1）如图，当点D在BC延长线上移动时，若∠BAC＝25°，则∠DCE＝　    　．

（2）设∠BAC＝α，∠DCE＝β．

①当点D在BC延长线上移动时，α与β之间有什么数量关系？请说明理由；

②当点D在直线BC上（不与B，C两点重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．

25．（14分）如图，已知△ABC中，AB＝AC＝6cm，BC＝4cm，点D为AB的中点．如果点P在线段BC上以1cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．

（1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；

（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

（3）若点Q以（2）中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？

八年级数学参考答案

一、选择题：（每题3分，共30分）

二、填空题：（每空2分，共16分）

13、       2a－4        14、     1      

15、    5         16、  （4，－1）或（－1，3）或（－1，－1）．

17、       180       18、     6  

19（1）解：a（1－4a）＋（2a＋1）（2a－1）

＝a－4a2＋4a2－1

＝a－1，

当a＝4时，原式＝4－1＝3．

（2）【解答】解：∵a、b、c为三角形三边的长，

∴a＋b＞c，a＋c＞b，b＋c＞a，

∴原式＝|a－（b＋c）|＋|b－（c＋a）|＋|（c＋b）－a|

＝b＋c－a＋a＋c－b＋c＋b－a

＝－a＋b＋3c．

20.【解答】（1）证明：∵AC∥DE，

∴∠ACB＝∠DEF，

∵BE＝CF，

∴BC＝EF，

在△ABC和△DFE中，

，

∴△ABC≌△DFE（AAS）．

（2）解：∵BF＝14，EC＝4，

∴BE＋CF＝14－4＝10，

∵BE＝CF，

∴BE＝CF＝5，

∴BC＝BE＋EC＝5＋4＝9．

21.【解答】解：（1）△ABE≌△ACD，

证明：∵AB＝AC，AE＝AD，∠BAC＝∠EAD＝90°，

∴∠BAC＋∠CAE＝∠EAD＋∠CAE，即∠BAE＝∠CAD，

∴△ABE≌△ACD（SAS）；

（2）由△ABE≌△ACD得∠ACD＝∠ABE＝45°，

又∵∠ACB＝45°，

∴∠BCD＝∠ACB＋∠ACD＝90°，

∴DC⊥BE．

22.【解答】（1）证明：

过E作EH⊥AB于H，EF⊥BC于F，EG⊥AD于G，

∵AD平分∠BAC，∠BAC＝120°，

∴∠BAD＝∠CAD＝60°，

∵∠CAH＝180°－120°＝60°，

∴AE平分∠HAD，

∴EH＝EG，

∵BE平分∠ABC，EH⊥AB，EF⊥BC，

∴EH＝EF，

∴EF＝EG，

∴点E到DA、DC的距离相等；

（2）解：∵由（1）知：DE平分∠ADC，

∴∠EDC＝∠DEB＋∠DBE，

∴＝∠DEB＋∠ABC，

∴∠DEB＝（∠CDA－∠ABC）＝∠BAD＝30°．

23.【解答】证明：（1）∵BD⊥MN，CE⊥MN，

∴∠BDA＝∠AEC＝90°，

∴∠BAD＋∠ABD＝90°，

又∵∠BAC＝90°，

∴∠BAD＋∠CAE＝90°，

∴∠ABD＝∠CAE；

（2）在△BAD和△ACE中

∵，

∴△BAD≌△ACE（AAS），

∴BD＝AE，AD＝CE，

又DE＝AE＋AD，

∴DE＝BD＋CE；

（3）DE＝CE－BD，

同（2）可得△BAD≌△ACE，

故BD＝AE，AD＝CE，

又DE＝AD－AE，

∴DE＝CE－BD．

24.【解答】（1）解：∵∠DAE＝∠BAC，

∴∠DAE＋∠CAD＝∠BAC＋∠CAD，

∴∠BAD＝∠CAE，

在△BAD和△CAE中

∵，

∴△BAD≌△CAE（SAS），

∴∠B＝∠ACE，

∵∠ACD＝∠B＋∠BAC＝∠ACE＋∠DCE，

∴∠BAC＝∠DCE，

∵∠BAC＝25°，

∴∠DCE＝25°，

故答案为：25°；

（2）①解：当点D在线段BC的延长线上移动时，α与β之间的数量关系是α＝β，理由是：

∵∠DAE＝∠BAC，

∴∠DAE＋∠CAD＝∠BAC＋∠CAD，

∴∠BAD＝∠CAE，

在△BAD和△CAE中

∵，

∴△BAD≌△CAE（SAS），

∴∠B＝∠ACE，

∵∠ACD＝∠B＋∠BAC＝∠ACE＋∠DCE，

∴∠BAC＝∠DCE，

∵∠BAC＝α，∠DCE＝β，

∴α＝β；

②解：当D在线段BC上时，α+β=180°；

当D在线段BC延长线或反向延长线时，α＝β

25.【解答】解：（1）全等，理由如下：

∵t＝1秒，

∴BP＝CQ＝1×1＝1厘米，

∵AB＝6cm，点D为AB的中点，

∴BD＝3cm．

又∵PC＝BC－BP，BC＝4cm，

∴PC＝4－1＝3cm，

∴PC＝BD．

又∵AB＝AC，

∴∠B＝∠C，

∴△BPD≌△CPQ；

（2）假设△BPD≌△CPQ，

∵vP≠vQ，

∴BP≠CQ，

又∵△BPD≌△CPQ，∠B＝∠C，则BP＝CP＝2，BD＝CQ＝3，

∴点P，点Q运动的时间t＝＝2秒，

∴vQ＝＝＝1.5cm/s；

（3）设经过x秒后点P与点Q第一次相遇，

由题意，得 1.5x＝x＋2×6，

解得x＝24，

∴点P共运动了24×1cm/s＝24cm．

∵24＝16＋4＋4，

∴点P、点Q在AC边上相遇，

∴经过24秒点P与点Q第一次在边AC上相遇．