人教版九年级上册21.2.2 公式法教学设计

21.2 .2一元二次方程的解法 公式法

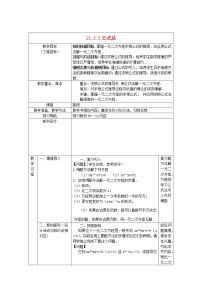
教学目标

1、使学生熟练地应用求根公式解一元二次方程。

2、使学生经历探索求根公式的过程，培养学生抽象思维能力。

3、在探索和应用求根公式中，使学生进一步认识特殊与一般的关系，渗透辩证唯物广义观点。

研讨过程

一、复习旧知，提出问题

1.用配方法解下列方程：

 （1）           (2)

2.用配方解一元二次方程的步骤是什么？

3.用直接开平方法和配方法解一元二次方程，计算比较麻烦，能否研究出一种更好的方法，迅速求得一元二次方程的实数根呢？

二、探索解法

问题1：能否用配方法把一般形式的一元二次方程转化为吗？

    因为，方程两边都除以，得                         

                           移项，得                         

                           配方，得                         

                         即                      

问题2：当，且时，大于等于零吗？

得出结论：当时，因为，所以，从而。

问题3：在研究问题1和问题2中，你能得出什么结论？

  得出结论，当时，一般形式的一元二次方程的根为，即。

    由以上研究的结果，得到了一元二次方程的求根公式： （）

       这个公式说明方程的根是由方程的系数、、所确定的，利用这个公式，我们可以由一元二次方程中系数、、的值，直接求得方程的解，这种解方程的方法叫做公式法。

       思考：当时，方程有实数根吗？

三、例题

例1、解下列方程：

  1、；                 2、；

  3、；                4、

  例2、解方程

       解：这里，，，

           因为负数不能开平方，所以原方程无实数根。

如：不解方程，判断下列方程根的情况：

（1）          （2）

四、课堂小结：

当时，方程有两个           的实数根；

当时，方程有两个        的实数根；

当时，方程         实数根。

五、课堂作业：

课本第17页习题21.2第4、5题。

六课后反思：

七、随堂检测

1.若关于的方程有实数解，则得取值范围是____

A.           B.

C.           D.

2. 方程的根是_____

A.        B.

C.无实根            D.

3. 如果关于的方程有两个相等的实数根，那么=______

4. 若关于的方程没有实数根，则得取值范围是______

5. 下列方程中，没有实数根的是_____

A.            B. 

C.             D. 

6. 已知两数的积是12，两数的平方和是25，则这两个数的和为______

7. 用公式法解一元二次方程。

（1）                  （2）