初中数学人教版七年级上册3.4 实际问题与一元一次方程教案设计

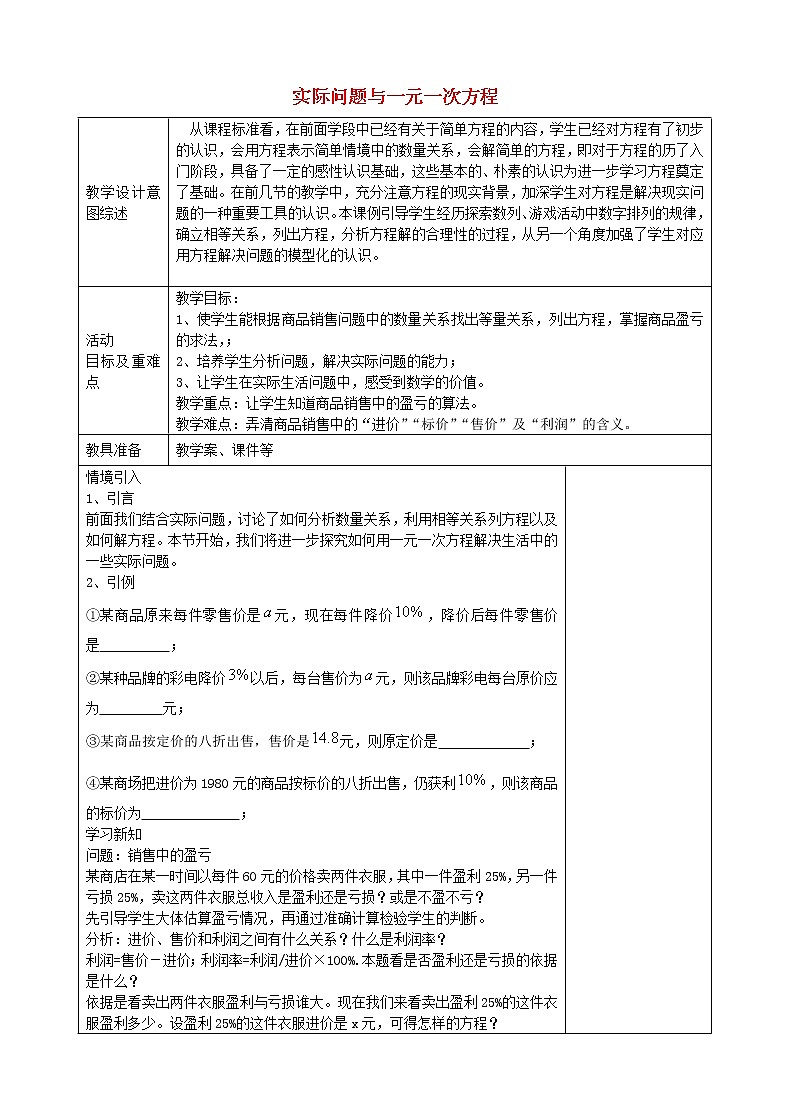
这是一份初中数学人教版七年级上册3.4 实际问题与一元一次方程教案设计，共2页。
实际问题与一元一次方程教学设计意图综述  从课程标准看，在前面学段中已经有关于简单方程的内容，学生已经对方程有了初步的认识，会用方程表示简单情境中的数量关系，会解简单的方程，即对于方程的历了入门阶段，具备了一定的感性认识基础，这些基本的、朴素的认识为进一步学习方程奠定了基础。在前几节的教学中，充分注意方程的现实背景，加深学生对方程是解决现实问题的一种重要工具的认识。本课例引导学生经历探索数列、游戏活动中数字排列的规律，确立相等关系，列出方程，分析方程解的合理性的过程，从另一个角度加强了学生对应用方程解决问题的模型化的认识。 活动目标及重难点教学目标：1、使学生能根据商品销售问题中的数量关系找出等量关系，列出方程，掌握商品盈亏的求法，；2、培养学生分析问题，解决实际问题的能力；3、让学生在实际生活问题中，感受到数学的价值。教学重点：让学生知道商品销售中的盈亏的算法。教学难点：弄清商品销售中的“进价”“标价”“售价”及“利润”的含义。教具准备教学案、课件等情境引入1、引言前面我们结合实际问题，讨论了如何分析数量关系，利用相等关系列方程以及如何解方程。本节开始，我们将进一步探究如何用一元一次方程解决生活中的一些实际问题。2、引例①某商品原来每件零售价是元，现在每件降价，降价后每件零售价是          ；②某种品牌的彩电降价以后，每台售价为元，则该品牌彩电每台原价应为         元；③某商品按定价的八折出售，售价是元，则原定价是             ；④某商场把进价为1980元的商品按标价的八折出售，仍获利，则该商品的标价为              ；学习新知问题：销售中的盈亏某商店在某一时间以每件60元的价格卖两件衣服，其中一件盈利25%，另一件亏损25%，卖这两件衣服总收入是盈利还是亏损？或是不盈不亏？先引导学生大体估算盈亏情况，再通过准确计算检验学生的判断。分析：进价、售价和利润之间有什么关系？什么是利润率？利润=售价－进价；利润率=利润/进价×100%.本题看是否盈利还是亏损的依据是什么？依据是看卖出两件衣服盈利与亏损谁大。现在我们来看卖出盈利25%的这件衣服盈利多少。设盈利25%的这件衣服进价是x元，可得怎样的方程？x+0.25x=60     解之，得x=48所以这件衣服利润是60－48=12元。再来看亏损25%的这件衣服亏损多少元。设亏损25%的这件衣服进价是y元，可得怎样的方程？        y－0.25y=60     解之，得y=80所以这件衣服的利润是60－80=－20元。因此，卖这两件衣服亏损了8元。注意：盈利时利润率通常用正数表示，所以亏损时利润率是负数。  例2  某种商品零售价每件900元，为了适应市场的竞争，商店按零售价的9折降价并让利40元销售，仍可获利10%，则这种商品进货每件多少元？分析：问题中的等量关系是什么？      实际售价－40－进价=利润。设这种子商品进货每件x元，那么实际售价是多少？利润是多少？实际售价是900×，利润是10%x。由此可得方程为    x+10%x=900×－40解之，得 x=700所以这种商品进货每件700元。 巩固练习由学生自主探索解决。问题1：一家商店将某种服装按成本价提高40%后标价，又以8折优惠卖出，结果每件仍获利15元，这种服装每件的成本是多少元？问题2：我国股市交易中每天、卖一次各交千分之七点五的各种费用，某投资者以每股10元的价格买入上海某股票1000股，当该股票涨到12元时全部卖出，该投资者实际盈利为多少？ 课堂小结1.由学生谈谈本节课学到了哪些知识？学后有何感受？2.商品销售中的基本等量关系有哪些？   利润=售价-进价   利润率= ×100%   打x折的售价=原售价×3.恰当地运用商品销售问题中的基本等量关系是解决这类问题的关键 作业：1、全能学案同步板书设计：  课后反思：