2021学年7.2 探索平行线的性质课文ppt课件

这是一份2021学年7.2 探索平行线的性质课文ppt课件，共21页。PPT课件主要包含了动手画一画，平行线的性质等内容，欢迎下载使用。

1、掌握平行线的性质定理：两直线平行，同位角相等。2、探索并证明平行线的性质定理：两直线平行，内错角相等（同旁内角互补），并能运用平行线的性质进行简单的推理、计算。3、经历探索直线平行线性质的过程，发展空间观念和有条理地表达能力。
1.应用性质进行简单的推理。
课堂练习：已知直线AB 及其外一点P，画出过点P的AB 的平行线.
问题：根据同位角相等可以判定两直线平行，反过来如果两直线平行同位角之间有什么关系呢？内错角，同旁内角之间又有什么关系呢？
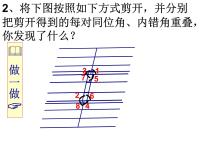
(1)用直尺和三角尺画出两条平行线 a∥b，再画一条截线c，使之与直线 a，b相交，并标出所形成的八角．(2)测量上面八个角的大小，记录下 来．从中你能发现什么？
如果两条直线平行，那么这两条平行线被第三条直线所截而成的同位角有什么数量关系？
平行线的性质1 两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.
如图，已知：a// b 那么3与2有什么关系？
平行线的性质2两条平行线被第三条直线所截，内错角相等 简单说成：两直线平行，内错角相等.
例如：如右图因为 a∥b，　　所以 ∠1= ∠2( )， 又 ∠3 = ___(对顶角相等)，　所以∠ 2 = ∠3.
两直线平行，同位角相等
如图：已知a//b，那么∠2与∠3有什么关系呢？
平行线的性质3 两条平行线被第三条直线所截，同旁内角互补 简单说成：两直线平行，同旁内角互补.
性质1：两直线平行，同位角相等． 性质2：两直线平行，内错角相等． 性质3：两直线平行，同旁内角互补．
例 如图7-15，AB ∥ CD，∠A=∠D．判断AF与ED的位置关系，并说明理由．
这样，由∠A=∠D、∠D=∠BED，可得∠A=∠BED.因为∠A=∠BED，所以AF ∥ED.理由是：同位角相等，两直线平行．
解：AF ∥ED因为AB ∥ CD，所以∠D=∠BED.理由是：两直线平行，内错角相等．
如图，直线a∥b， ∠1=54°，∠2， ∠3， ∠4各是多少度？
∵ ∠2=∠1 (对顶角相等)∴ ∠2=∠1 =54°∵ a∥b(已知)∴ ∠4=∠1=54°(两直线平行，同位角相等) ∠2+∠3=180°(两直线平行，同旁内角互补)∴ ∠3= 180°－ ∠2= 180° － 54°=126°
（1）∵∠ADE=60 ° ∠B=60 °
(同位角相等，两直线平行)
(两直线平行，同位角相等)
已知∠ADE=60°，∠B=60°，∠AED=40°.证：（1）DE∥BC （2） ∠C的度数
如图：已知 ∠1= ∠2求证：∠BCD+ ∠D=180°
1.如图，l1∥l2，l3⊥l1.l3与l2有怎样的位置关系？
l3⊥l2，根据两直线平行，同位角相等.
2.如图，CD∥EF，DE∥AC.图中哪些角相等？为什么？
∠BFE=∠FDC，∠BEF=∠ECD，∠DEF=∠EDC=∠DCA, ∠A=∠BDE，∠BED=∠ECA.因为两直线平行，同位角相等，内错角相等.
3.如图，点B、C、D在一条直线上，AB∥EC，∠A=55°，∠B=60°.求∠1、∠2和∠ACB的度数.
∵AB∥EC，∴∠1=∠A=55°，∠2=∠B=60°，∠ACB=180°-∠A-∠B=65°.
两直线平行同旁内角互补