初中数学苏科版九年级上册1.4 用一元二次方程解决问题教学设计

这是一份初中数学苏科版九年级上册1.4 用一元二次方程解决问题教学设计，共4页。教案主要包含了情境引入，探究学习，归纳总结等内容，欢迎下载使用。

主备人
学 科
主备时间
集体备课时间
执教人
执教时间
执教班级
教 时
课题
4.3用一元二次方程解决问题（3）
教学
目标
１、掌握列出一元二次方程解应用题；并能根据具体问题的实际意义，检验结果的合理性；
２、理解将一些实际问题抽象为方程模型的过程，学会从数学的角度提出问题、理解问题，并能运用所学的知识解决问题。
教学重难点
重点：学会用列方程的方法解决有关形积问题．
难点：如何找出形积问题中的等量关系
教具
多媒体 教材 相关资料
教法
合作探究 启发引导
一次备课
集体备课
教学过程
一、情境引入：
问题、一根长22cm的铁丝。
（1）能否围成面积是30的矩形？
（2）能否围成面积是32 的矩形？并说明理由。
二、探究学习：
1．尝试：下面数量之间的关系吗？
如果设这根铁丝围成的矩形的长是x，你能用数学式子表示矩形的宽吗？
你能找出这个问题中的相等关系吗？
相等关系： 。
2．概括总结．
列方程的关系是找出相等关系。
3.典型例题：
例题1、如图所示
（1）小明家要建面积为150m2的养鸡场，鸡场一边靠墙，另一边用竹篱笆围成，竹篱笆总长为35m。若墙的长度为18m，鸡场的长、宽分别是多少？
（2）如果墙的长为15m，鸡场一边靠墙，竹篱笆总长为45m。
 可围成的鸡场的面积能达到250m2吗？通过计算说明理由。
可围成的鸡场的面积能达到100m2吗？通过计算并画草图说明。
（3）可如果墙的长为15m，鸡场一边靠墙，竹篱笆总长为45m，可围成的鸡场最大面积是多少平方米？
例题2如图，在矩形ABCD中，AB=6 cm，BC=12 cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，（1）几秒后△PBQ的面积等于8 cm2？
（2）△PDQ的面积能为8cm2吗?为什么?
4.巩固练习：
（1）用长为100 cm的金属丝制作一个矩形框子。框子各边多长时，框子的面积是600 cm2？能制成面积是800 cm2的矩形框子吗？
（2）如图，在矩形ABCD中，AB=6cm，BC=3cm。点P沿边AB从点A开始向点B以2cm/s的速度移动，点Q沿边DA从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤3）。那么，当t为何值时，△QAP的面积等于2cm2?
（3）如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度为a为15米），围成中间隔有一道篱笆的长方形花圃。
①如果要围成面积为45平方米的花圃，AB的长是多少米？
②能围成面积比45平方米更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由。
（4）、把一根长为80cm的绳子剪成两段，并把每一段绳子围成一个正方形。
①要使这两个正方形的面积之和等于200cm2, 该怎么剪？
②这两个正方形面积之和可能等于488cm2吗？
三、归纳总结：
1、通常用一元二次方程解决实际问题要经历怎样的过程？
2、用一元二次方程解决实际问题的关键是什么？
【课后作业】
1、用长为100 cm的金属丝制作一个矩形框子。框子各边多长时，框子的面积是600 cm2？能制成面积是800 cm2的矩形框子吗？
2．如图，A、B、C、D为矩形的四个顶点，AB=16cm，BC=6cm，动点P、Q分别从点A、C出发，点P以3cm/s的速度向点B移动，一直到达B为止；点Q以2cm/s的速度向点D移动。经过多长时间P、Q两点之间的距离是10cm？
3．如图，在Rt△ABC中，AB=BC=12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC，问点D出发几秒后四边形DFCE的面积为20cm2？
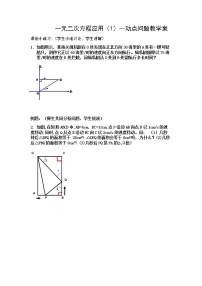
4．如图所示，人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处的位置O点的正北方向10海里外的A点有一涉嫌走私船只正以24海里/时的速度向正东方向航行，为迅速实施检查，巡逻艇调整好航向，以26海里/时的速度追赶。在涉嫌船只不改变航向和航速的前提下，问需要几小时才能追上（点B为追上时的位置）？
5．如图，把长AD=10cm，宽AB=8cm的矩形沿着AE对折，使D点落在BC边的F点上，求DE的长。
【教学反思】