人教版九年级下册第二十七章 相似27.1 图形的相似图文ppt课件

这是一份人教版九年级下册第二十七章 相似27.1 图形的相似图文ppt课件，共29页。PPT课件主要包含了教学目标，情境导入，合作探究，探究一相似图形，图形的放大，图形的缩小，典例精析，趁热打铁，探究二成比例线段，内项积＝外项积等内容，欢迎下载使用。
1.了解相似图形的概念.2. 理解相似多边形和相似比的定义.3. 能根据多边形相似进行相关边长、角度的计算，会根据条件判断两个多边形是否相似. (重点、难点)
下图中有汽车和它的模型，有大小不同的足球，还有同一张底版洗出的不同尺寸的照片，以及排版印刷时使用不同字号排出的相同文字，所有这些给我们什么样的形象？
形状相同的图形叫做相似图形.
相似图形的大小不一定相同.
相似图形的关系：两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到。
思考1：你见过哈哈镜吗？哈哈镜与平面镜中的形象哪一个与你本人相似？
平面镜的形象与本人相似。
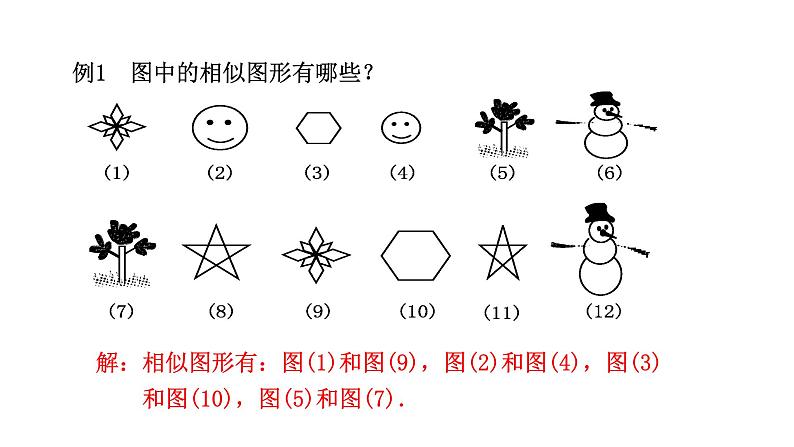
例1　图中的相似图形有哪些？
解：相似图形有：图(1)和图(9)，图(2)和图(4)，图(3) 和图(10)，图(5)和图(7)．
1、放大镜下的图形和原来的图形相似吗？
2、 观察下面的图形 (a)~(e)，其中哪些是与图形 (1)或 (2) 相似的？
归纳总结：(1)两个图形相似是指它们的形状相同，与它们的位置无关；(2)全等图形是一种特殊的相似图形，不仅形状相同，大小也相同．
在四条线段 a、b、c、d 中，如果 a 和 b 的比等于 c 和 d 的比，那么这四条线段a、b、c、d 叫做成比例线段， 简称比例线段.
a ：b = c ：d
1、下列四组长度中的四条线段能成比例的是（ ）
A. 1 cm，2 cm，3 cm，4 cm B. 2 cm，4 cm，6 cm，8 cm C. 5 cm，30 cm，10 cm，15 cm D. 5 cm，10 cm，15 cm，20 cm
2、四条线段a，b，c，d成比例(即 )，其中a＝3 cm，d＝4 cm，c＝6 cm，则b等于(　　) A．8 cm B. cm C. cm D．2 cm
图中的两个大小不同的四边形ABCD和四边形A1B1C1D1中，∠A=∠A1，∠B=∠B1，∠C=∠C1，∠D=∠D1， 因此四边形ABCD与四边形A1B1C1D1相似.
★相似多边形的定义（判定）：
思考2：任意两个等边三角形相似吗？任意两个正方形呢？任意两个正 n 边形呢？
知识点拨：已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等，对应角相等，以及对应边的比相等.
同理，任意两个正方形都相似.
归纳：任意两个边数相等的正多边形都相似.
例1 如图，四边形 ABCD 和 EFGH 相似，求角α，β的大小和EH 的长度 x.
在四边形ABCD中，β＝360°－(78°＋83°＋118°)＝81°.
∠α＝∠C＝83°，∠A＝∠E＝118°.
解：∵ 四边形 ABCD 和 EFGH 相似，∴ 它们的对应角相等．由 此可得:
∵ 四边形ABCD和四边形EFGH相似，∴它们的对应边成比例，由此可得:
解得: x ＝ 28 cm.
1、如图所示的两个三角形相似吗？为什么？
解：相似. 由已知条件可知它们的角分别相等，边成比例.
2、如图所示的两个五边形相似，求未知边 a，b， c，d 的长度．
解：相似多边形的对应边的比相等，由此可得
解得：a=3，b=4.5，c=4，d=6.所以未知边a，b，c，d的长度分别为3，4.5，4，6.
1、下列说法中正确的是(　　) A．对应角相等的多边形一定是相似多边形 B．对应边的比相等的多边形是相似多边形 C．边数相同的多边形是相似多边形 D．对应角相等、对应边成比例的两个边数相同的多边形是 相似多边形
2、两个等边三角形，两个矩形，两个正方形，两个菱形各成一组，每组中的一个图形在另一个图形的内部，对应边平行，且对应边之间的距离都相等，那么两个图形不相似的一组是(　　)
3、若一张地图的比例尺是 1:150000，在地图上量得甲、乙两地的距离是 5 cm，则甲、乙两地的实际距离是（ ）
A. 3000 m B. 3500 m C. 5000 m D. 7500 m
4、六边形ABCDEF与六边形A′B′C′D′E′F′相似，若对应边AB与A′B′的长分别为50 cm和20 cm，则六边形A′B′C′D′E′F′与六边形ABCDEF的相似比是(　　) A．5:2 B．2:5 C．5:1 D．1:
知识点拨：判定相似比有顺序性。
5、若一个三角形的三边之比为3:5:7，与它相似的三角形的最长边的长为21，则最短边的长为(　　)A．15 B．10 C．9 D．3
6、如图，在三个矩形中，相似的是(　　) A．甲和丙 B．甲和乙 C．乙和丙 D．甲、乙和丙
知识点拨：判定相似多边形的条件：(1)所有的角分别相等；(2)所有的边成比例．缺一不可．
7. 填空：(1) 如图①是两个相似的四边 形，则x= ， y = ， α= ；(2) 如图②是两个相似的矩形， x= .
解：(1)设AD＝x，则DM＝ . ∵矩形DMNC与矩形ABCD相似， ∴x2＝32. ∴x＝4 或x＝－4 (舍去)，即AD的长为4 . (2)矩形DMNC与矩形ABCD的相似比为
8、如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB＝4.(1)求AD的长； (2)求矩形DMNC与矩形ABCD的相似比．
9、如图，G是正方形ABCD对角线AC上一点，作GE⊥AD, GF⊥AB，垂足分别为点E，F. 求证：四边形AFGE与四边形ABCD相似．
证明：∵四边形ABCD是正方形，∴AB＝BC＝CD＝DA， ∠DAC＝∠BAC＝45°.又∵GE⊥AD，GF⊥AB， ∴EG＝FG，且AE＝EG，AF＝FG. ∴AE＝EG＝FG＝AF，∴四边形AFGE为正方形． ∴ ，且∠EAF＝∠DAB， ∠AFG＝∠ABC，∠FGE＝∠BCD，∠AEG＝∠ADC. ∴四边形AFGE与四边形ABCD相似．