初中数学湘教版九年级上册2.2 一元二次方程的解法集体备课课件ppt

这是一份初中数学湘教版九年级上册2.2 一元二次方程的解法集体备课课件ppt，共18页。PPT课件主要包含了学习目标，导入新课，复习引入，讲授新课，合作探究，求根公式的推导，移项得，配方得，特别提醒，因此方程无实数根等内容，欢迎下载使用。

1.理解一元二次方程求根公式的推导过程；2.会用公式法解一元二次方程；（重点）3.会用根的判别式b2-4ac判断一元二次方程根的情况及相关应用.（难点）
1.用配方法解一元二次方程的步骤有哪几步？
2.如何用配方法解方程2x2+4x+1=0?
任何一个一元二次方程都可以写成一般形式 ax2+bx+c=0 能否也用配方法得出它的解呢？
用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
方程两边都除以a
问题：接下来能用直接开平方解吗？
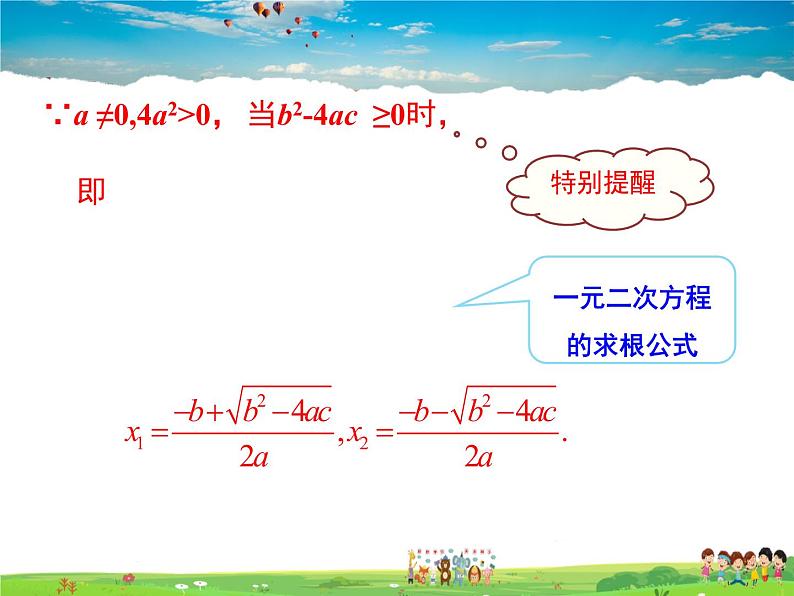
一元二次方程的求根公式
∵a ≠0,4a2>0，
当b2-4ac ≥0时，
当b2-4ac ＜0时，
而x取任何实数都不能使上式成立.
由上可知，一元二次方程ax2+bx+c=0 (a≠0)的根由方程的系数a，b，c确定．因此，解一元二次方程时，可以先将方程化为一般形式ax2+bx+c=0 (a≠0) ，当b2-4ac ≥0 时，将a，b，c 代入式子 就得到方程的根，这个式子叫做一元二次方程的求根公式，利用它解一元二次方程的方法叫做公式法，由求根公式可知，一元二次方程最多有两个实数根.
例1：解方程：x2-2x-2=0
解：这里 a=1, b= -1, c= -2.
∵ b 2 - 4a c =(-1)2 - 4×1×(-28)=9﹥0,
即：x1=2, x2= -1.
例 2 ：解方程：9x2+12x+4=0
解：这里a=9,b=12,c=4因而 b2-4ac=122-4×9×4=0所以因此，原方程的根为
1. 用公式法解方程 5x2-4x-12=0
解：∵a=5,b=-4,c=-12，
b2-4ac=(-4)2-4×5×(-12)=256>0.
这里的a、b、c的值是什么？
例3 解方程：4x2-3x+2=0
因为在实数范围内负数不能开平方，所以方程无实数根.
1.变形: 化已知方程为一般形式; 2.确定系数:用a,b,c写出各项系数;3.计算: b2-4ac的值; 4.判断：若b2-4ac ≥0，则利用求根公式求出; 若b2-4ac<0，则方程没有实数根.
1.解方程：x2 +7x – 18 = 0.
解：这里 a=1, b= 7, c= -18. ∵ b 2 - 4ac =7 2 – 4 × 1× (-18 ) =121>0, 即 x1 = -9, x2 = 2 .
2. 解方程（x - 2) (1 - 3x) = 6.
解：去括号 ，得 x –2 - 3x2 + 6x = 6, 化简为一般式 3x2 - 7x + 8 = 0, 这里 a = 3, b = -7 , c = 8. ∵b2 - 4ac=(-7 )2 – 4 × 3 × 8 = 49–96 = - 47 < 0, ∴原方程没有实数根.
3. 解方程：2x2 - x + 3 = 0 解： 这里 a = 2 , b = , c = 3 . ∵ b2 - 4ac = 27 - 4×2×3 = 3 > 0 , ∴ 即 x1= x2=