苏科版八年级上册1.3 探索三角形全等的条件教案配套ppt课件

这是一份苏科版八年级上册1.3 探索三角形全等的条件教案配套ppt课件，共11页。PPT课件主要包含了SSS，ASA，AAS，SAS，导入新课，讲授新课，证明过程如下，PCPD，当堂练习，∴BFDE等内容，欢迎下载使用。

2.判别两个三角形全等的方法:
1.全等三角形的性质：
对应角相等，对应边相等.
用“HL”判定三角形全等
我们已经知道，三边对应相等的两个三角形全等.由勾股定理可知：两边对应相等的两个直角三角形，其第三条也一定相等.
在一个三角形中，由勾股定理可知：如果两条边确定，那么第三条也随之确定.由此可以得出直角三角形的新的判定方法.
因此，斜边和第三边对应相等的两个直角三角形全等.
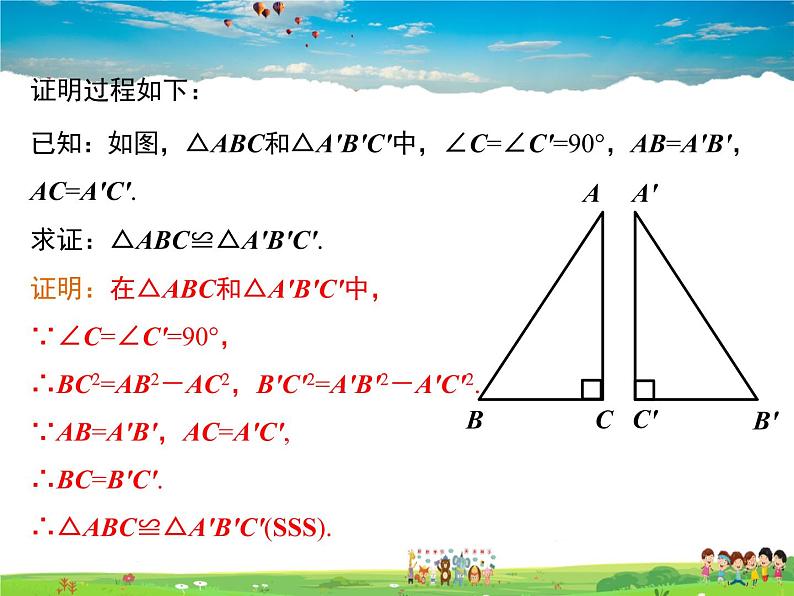
已知：如图，△ABC和△A'B'C'中，∠C=∠C'=90°，AB=A'B'，AC=A'C'.
求证：△ABC≌△A'B'C'.
证明：在△ABC和△A'B'C'中，∵∠C=∠C'=90°，∴BC2=AB2－AC2，B'C'2=A'B'2－A'C'2.∵AB=A'B'，AC=A'C',∴BC=B'C'.∴△ABC≌△A'B'C'(SSS).
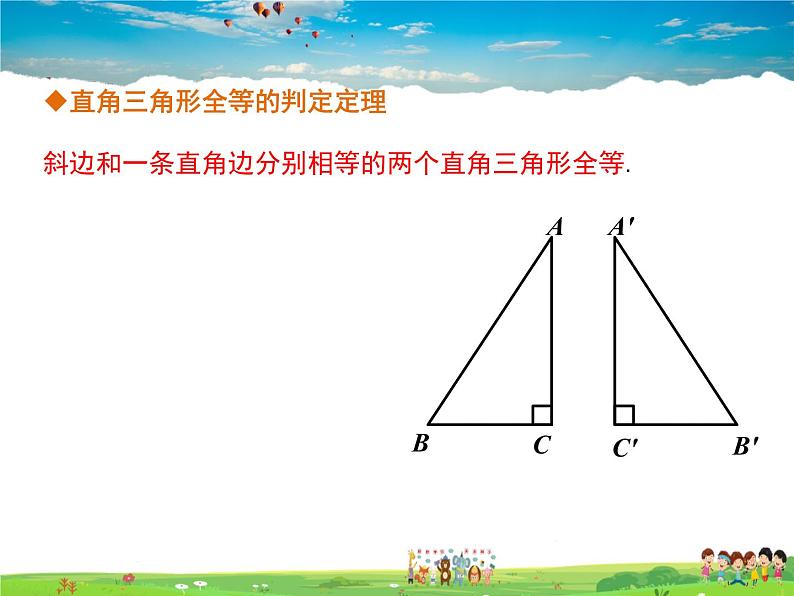
直角三角形全等的判定定理
斜边和一条直角边分别相等的两个直角三角形全等.
例1 如图，AC⊥BC， BD⊥AD， AC﹦BD，求证：BC﹦AD.
证明： ∵ AC⊥BC， BD⊥AD， ∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中，
∴ Rt△ABC≌Rt△BAD (HL).∴ BC﹦AD(全等三角形的对应边相等).
例2 已知：如图，点P在∠AOB的内部，PC⊥OA，PD⊥OB，垂足分别为C，D，PC=PD.求证：点P在∠AOB的平分线上.
证明：如图作射线OP，∵PC⊥OA，PD⊥OB，∴∠PCO=∠PDO=90°.在△OPC和△OPD中，
OP=OP（公共边），
∴Rt△ABC≌Rt△A'B'C'(HL).
∴∠POA=∠POB，∴点P在∠AOB的平分线上.
1. 如图，∠B=∠D=90°，要证明△ABC 与△ADC全等，还需要补充的条件是 （写出一个即可）.
答案： AB=AD 或 BC=DC 或 ∠BAC=∠DAC 或 ∠ACB=∠ACD.
2.如图 在△ABC中，已知BD⊥AC，CE ⊥AB，BD=CE.求证：△EBC≌△DCB.
证明： ∵ BD⊥AC，CE⊥AB， ∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中，
∴ Rt△EBC≌Rt△DCB (HL).
3.如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证：BF=DE.
证明: ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.∵AE=CF， ∴AE+EF=CF+EF.即AF=CE.在Rt△ABF和Rt△CDE中，
∴ Rt△ABF≌Rt△CDE(HL).