2021-2022学年新疆阿克苏地区沙雅三中九年级（上）期中数学试卷（解析版）

2017-2018学年新疆阿克苏地区沙雅三中九年级（上）期中数学试卷

一、选择题（每小题3分，共30分）

1．（3分）有下列关于x的方程是一元二次方程的是（　　）

A．3x（x﹣4）=0 B．x2+y﹣3=0 C． +x=2 D．x3﹣3x+8=0

2．（3分）方程3x2﹣8x﹣10=0的二次项系数和一次项系数分别为（　　）

A．3和8 B．3和﹣8 C．3和﹣10 D．3和10

3．（3分）下列标志既是轴对称图形又是中心对称图形的是（　　）

A． B． C． D．

4．（3分）当ab＞0时，y=ax2与y=ax+b的图象大致是（　　）

A． B． C． D．

5．（3分）抛物线y=x2﹣4x﹣5的顶点在第（　　）象限．

A．一 B．二 C．三 D．四

6．（3分）一元二次方程x2+x+=0的根的情况是（　　）

A．有两个不等的实数根 B．有两个相等的实数根

C．无实数根 D．无法确定

7．（3分）若α、β是方程x2+2x﹣2017=0的两个实数根，则α•β的值为（　　）

A．2017 B．2 C．﹣2 D．﹣2017

8．（3分）二次函数y=（x+1）2+2的最小值是（　　）

A．2 B．1 C．﹣3 D．

9．（3分）方程x2=x的解是（　　）

A．x=1 B．x=0 C．x1=﹣1，x2=0 D．x1=1，x2=0

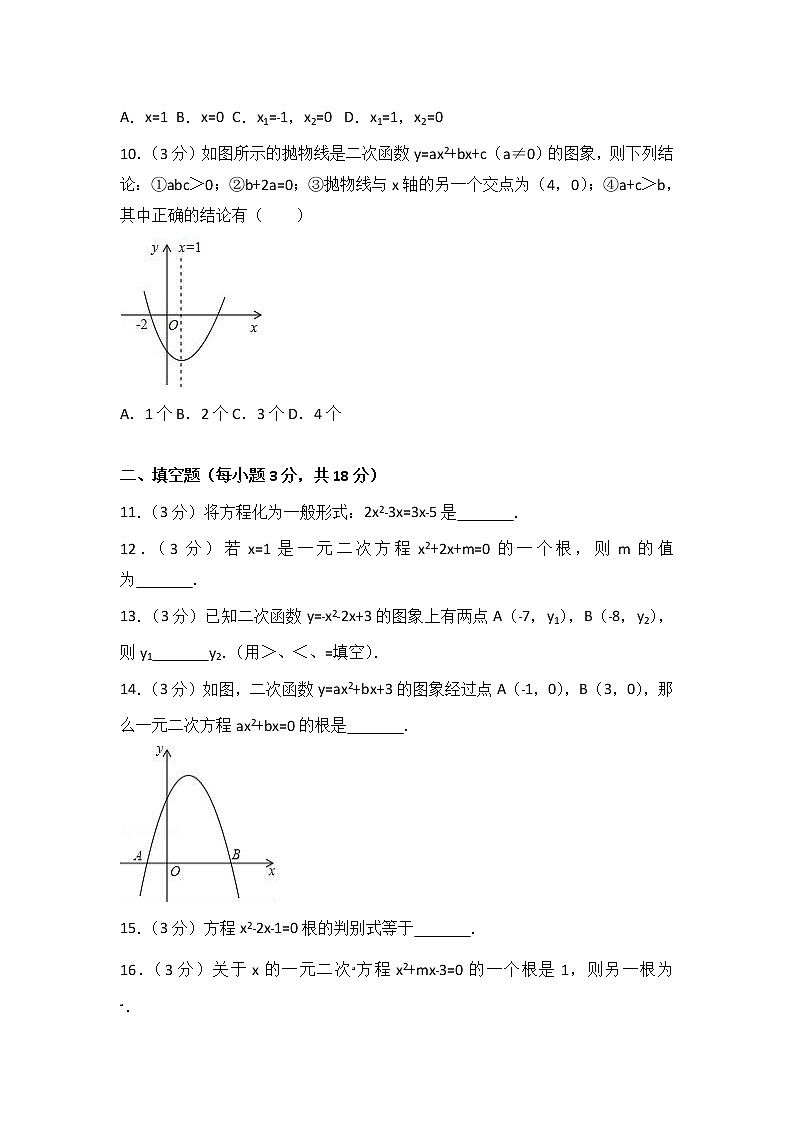
10．（3分）如图所示的抛物线是二次函数y=ax2+bx+c（a≠0）的图象，则下列结论：①abc＞0；②b+2a=0；③抛物线与x轴的另一个交点为（4，0）；④a+c＞b，其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个

二、填空题（每小题3分，共18分）[来源:学科网ZXXK]

11．（3分）将方程化为一般形式：2x2﹣3x=3x﹣5是　   　．[来源:Zxxk.Com]

12．（3分）若x=1是一元二次方程x2+2x+m=0的一个根，则m的值为　   　．

13．（3分）已知二次函数y=﹣x2﹣2x+3的图象上有两点A（﹣7，y1），B（﹣8，y2），则y1　   　y2．（用＞、＜、=填空）．

14．（3分）如图，二次函数y=ax2+bx+3的图象经过点A（﹣1，0），B（3，0），那么一元二次方程ax2+bx=0的根是　   　．

15．（3分）方程x2﹣2x﹣1=0根的判别式等于　   　．

16．（3分）关于x的一元二次方程x2+mx﹣3=0的一个根是1，则另一根为　   　．

三、解答题．（共52分）

17．（10分）解方程．[来源:学,科,网Z,X,X,K]

（1）x2﹣3x﹣4=0

（2）（x﹣3）2=3x（x﹣3）

18．（8分）在实数范围内定义一种新运算“△”，其规则为：a△b=a2﹣b2，根据这个规则：

（1）求4△3的值；

（2）求（x+2）△5=0中x的值．

19．（9分）如图，抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C （0，3）三点，直线l是抛物线的对称轴．

（1）求抛物线的函数关系式；

（2）求出抛物线的顶点坐标，对称轴及二次函数的最大值．

20．（9分）已知关于x的一元二次方程x2﹣mx﹣2=0．

（1）对于任意实数m，判断此方程根的情况，并说明理由；

（2）当m=2时，求方程的根．

21．（8分）如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m，另一边减少了3m，剩余一块面积为20m2的矩形空地，求原正方形空地的边长．

[来源:学科网ZXXK]

22．（8分）某宾馆有50个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．房价定为多少时，宾馆利润最大？

2017-2018学年新疆阿克苏地区沙雅三中九年级（上）期中数学试卷

参考答案与试题解析

一、选择题（每小题3分，共30分）

1．（3分）有下列关于x的方程是一元二次方程的是（　　）

A．3x（x﹣4）=0 B．x2+y﹣3=0 C． +x=2 D．x3﹣3x+8=0

【解答】解：A、是一元二次方程，故此选项正确；

B、不是一元二次方程，故此选项错误；

C、不是一元二次方程，故此选项错误；

D、不是一元二次方程，故此选项错误；

故选：A．

2．（3分）方程3x2﹣8x﹣10=0的二次项系数和一次项系数分别为（　　）

A．3和8 B．3和﹣8 C．3和﹣10 D．3和10

【解答】解：3x2﹣8x﹣10=0的二次项系数和一次项系数分别为3，﹣8，

故选：B．

3．（3分）下列标志既是轴对称图形又是中心对称图形的是（　　）

A． B． C． D．

【解答】解：A、是轴对称图形，也是中心对称图形；

B、是轴对称图形，不是中心对称图形；

C、不是轴对称图形，是中心对称图形；

D、不是轴对称图形，也不是中心对称图形．

故选：A．

4．（3分）当ab＞0时，y=ax2与y=ax+b的图象大致是（　　）

A． B． C． D．

【解答】解：根据题意，ab＞0，即a、b同号，

当a＞0时，b＞0，y=ax2与开口向上，过原点，y=ax+b过一、二、三象限；

此时，没有选项符合，

当a＜0时，b＜0，y=ax2与开口向下，过原点，y=ax+b过二、三、四象限；

此时，D选项符合，

故选：D．

5．（3分）抛物线y=x2﹣4x﹣5的顶点在第（　　）象限．

A．一 B．二 C．三 D．四

【解答】解：抛物线y=x2﹣4x﹣5的顶点坐标为：x=﹣=2，y==﹣9，即（2，﹣9），

∵2＞0，﹣9＜0，

∴顶点在第四象限．

故选：D．

6．（3分）一元二次方程x2+x+=0的根的情况是（　　）

A．有两个不等的实数根 B．有两个相等的实数根

C．无实数根 D．无法确定

【解答】解：∵△=b2﹣4ac=12﹣4•1•=0，

∴原方程有两个相等的实数根．

故选：B．

7．（3分）若α、β是方程x2+2x﹣2017=0的两个实数根，则α•β的值为（　　）

A．2017 B．2 C．﹣2 D．﹣2017

【解答】解：∵α、β是方程x2+2x﹣2017=0的两个实数根，

∴α•β=﹣2017．

故选：D．

8．（3分）二次函数y=（x+1）2+2的最小值是（　　）

A．2 B．1 C．﹣3 D．

【解答】解：由二次函数的解析式可知此函数的最小值是2．

故选：A．

9．（3分）方程x2=x的解是（　　）

A．x=1 B．x=0 C．x1=﹣1，x2=0 D．x1=1，x2=0

【解答】解：x2=x，

移项得x2﹣x=0，

提公因式得x（x﹣1）=0，

解得x1=1，x2=0．

故选：D．

10．（3分）如图所示的抛物线是二次函数y=ax2+bx+c（a≠0）的图象，则下列结论：①abc＞0；②b+2a=0；③抛物线与x轴的另一个交点为（4，0）；④a+c＞b，其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个

【解答】解：∵抛物线开口向上，

∴a＞0，

∵抛物线的对称轴为直线x=﹣=1，

∴b=﹣2a＜0，所以②正确；

∵抛物线与y轴的交点在x轴下方，

∴c＜0，

∴abc＞0，所以①正确；

∵点（﹣2，0）关于直线x=1的对称点的坐标为（4，0），

∴抛物线与x轴的另一个交点坐标为（4，0），所以③正确；

∵x=﹣1时，y＜0，

即a﹣b+c＜0，

∴a+c＜b，所以④错误．

故选：C．

二、填空题（每小题3分，共18分）

11．（3分）将方程化为一般形式：2x2﹣3x=3x﹣5是　2x2﹣6x+5=0　．

【解答】解：2x2﹣3x=3x﹣5是一般形式是2x2﹣6x+5=0，

故答案为：2x2﹣6x+5=0．

12．（3分）若x=1是一元二次方程x2+2x+m=0的一个根，则m的值为　﹣3　．

【解答】解：将x=1代入得：1+2+m=0，

解得：m=﹣3．

故答案为：﹣3．

13．（3分）已知二次函数y=﹣x2﹣2x+3的图象上有两点A（﹣7，y1），B（﹣8，y2），则y1　＞　y2．（用＞、＜、=填空）．

【解答】解：∵二次函数y=﹣x2﹣2x+3的对称轴是x=﹣1，开口向下，

∴在对称轴的左侧y随x的增大而增大，

∵点A（﹣7，y1），B（﹣8，y2）是二次函数y=﹣x2﹣2x+3的图象上的两点，

﹣7＞﹣8，

∴y1＞y2．

故答案为：＞．[来源:Z。xx。k.Com]

14．（3分）如图，二次函数y=ax2+bx+3的图象经过点A（﹣1，0），B（3，0），那么一元二次方程ax2+bx=0的根是　x1=0，x2=2　．

【解答】解：把A（﹣1，0），B（3，0）代入y=ax2+bx+3

得，

解得，

代入ax2+bx=0

得，﹣x2+2x=0，

解得x1=0，x2=2．

故答案为：x1=0，x2=2．

15．（3分）方程x2﹣2x﹣1=0根的判别式等于　8　．

【解答】解：由题意得：a=1，b=﹣2，c=﹣1，

△=b2﹣4ac=（﹣2）2﹣4×1×（﹣1）=8，

故答案为：8．

16．（3分）关于x的一元二次方程x2+mx﹣3=0的一个根是1，则另一根为　﹣3　．

【解答】解：根据题意可得

x1+x2=﹣=﹣m，x1x2==﹣3，

∵x1=1，

∴1+x2=﹣m，x2=﹣3，

∴m=2．

故答案为：﹣3

三、解答题．（共52分）

17．（10分）解方程．

（1）x2﹣3x﹣4=0

（2）（x﹣3）2=3x（x﹣3）

【解答】解：（1）x2﹣3x﹣4=0，

（x﹣4）（x+1）=0，

x﹣4=0，x+1=0，

x1=4，x2=﹣1；

（2）（x﹣3）2=3x（x﹣3），

（x﹣3）2﹣3x（x﹣3）=0，

（x﹣3）（x﹣3﹣3x）=0，

x﹣3=0，x﹣3﹣3x=0，

x1=3，x2=﹣1.5．

18．（8分）在实数范围内定义一种新运算“△”，其规则为：a△b=a2﹣b2，根据这个规则：

（1）求4△3的值；

（2）求（x+2）△5=0中x的值．

【解答】解：（1）4△3=42﹣32=16﹣9=7；

（2）由题意得：（x+2）2﹣25=0，

（x+2）2=25，

x+2=±5，

x+2=5或x+2=﹣5，

解得：x1=3，x2=﹣7．

19．（9分）如图，抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C （0，3）三点，直线l是抛物线的对称轴．

（1）求抛物线的函数关系式；

（2）求出抛物线的顶点坐标，对称轴及二次函数的最大值．

【解答】解：（1）设抛物线解析式为y=a（x+1）（x﹣3），

把C（0，3）代入得a•1•（﹣3）=3，解得a=﹣1，

所以抛物线解析式为y=﹣（x+1）（x﹣3）=﹣x2+2x+3；

（2）y=﹣x2+2x+3=﹣（x﹣1）2+4，

所以抛物线的顶点坐标为（1，4），对称轴为：直线x=1，二次函数的最大值是4．

20．（9分）已知关于x的一元二次方程x2﹣mx﹣2=0．

（1）对于任意实数m，判断此方程根的情况，并说明理由；

（2）当m=2时，求方程的根．

【解答】解：（1）对于任意实数m，方程总有两个不相等的实数根，利用如下：

∵△=（﹣m）2﹣4×1×（﹣2）=m2+8＞0，

∴对于任意实数m，方程总有两个不相等的实数根．

（2）当m=2时，原方程为x2﹣2x﹣2=0，

此时△=m2+8=12，

∴x1=1﹣，x2=1+．

21．（8分）如图，将一块正方形空地划出部分区域进行绿化，原空地一边减少了2m，另一边减少了3m，剩余一块面积为20m2的矩形空地，求原正方形空地的边长．

【解答】解：设原正方形的边长为xm，依题意有

（x﹣3）（x﹣2）=20，

解得：x1=2，x2=3．

经检验，x=2不符合题意，舍去

答：原正方形的边长3m．

22．（8分）某宾馆有50个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．房价定为多少时，宾馆利润最大？

【解答】解：设房价为（180+10x）元，则定价增加了10x元，此时空闲的房间为x，

由题意得，y=（180+10x）（50﹣x）﹣（50﹣x）×20=﹣10x2+340x+8000=﹣10（x﹣17）2+10890

故可得当x=17，即房间定价为180+170=350元的时候利润最大．

答：房间定价为350元时，利润最大．