数学人教版第二十四章 圆24.4 弧长及扇形的面积精品第1课时课后练习题

自我小测

复习巩固

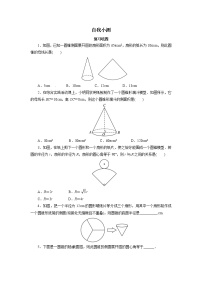
1．如图，已知O的半径OA＝6，∠AOB＝90°，则∠AOB所对的弧AB的长为(　　)

A．2π　　　　　B．3π

C．6π          D．12π

2．如果某钟表的轴心到分针外端点的长为5cm，那么经过40 min，分针外端点转过的弧长是(　　)

A．cm        B．cm

C．cm        D．cm

3．已知圆上一段弧长为5π，它所对的圆心角为100°，则该圆的半径为(　　)x k b 1 . c o m

A．6         B．9        C．12        D．18

4．如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”．则半径为2的“等边扇形”的面积为(　　)

A．π         B．1

C．2         D．

5．如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为120°，AB的长为30cm，贴纸部分BD的长为20cm，则贴纸部分的面积为(　　)

A．100πcm2        B．πcm2

C．800πcm2        D．πcm2

6．在半径为的圆中，45°的圆心角所对的弧长等于__________．

7．若一扇形的面积为12π，半径等于6，则它的圆心角等于______．

8．如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于__________.

xkb1.com

9．如图，AB是半圆O的直径，AB＝2R，C，D为该半圆的三等分点，求阴影部分的面积．

能力提升

10．如图，有一长为4cm，宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向)，木板上的顶点A的位置变化为A→A1→A2，其中第二次翻滚被桌面上一小木块挡住，使木板边沿A2C与桌面成30°角，则点A翻滚到A2位置时，共走过的路径长为(　　)

A．10cm         B．3.5πcm        C．4.5πcm        D．2.5πcm

11．如图所示，扇形AOB的圆心角为120°，半径为2，则图中阴影部分的面积为(　　)

A．        B．

C．        D．

12．如图，分别以Rt△ABC的三边AB，BC，CA为直径向外作半圆，AB左边阴影部分的面积为S1，右边阴影部分的面积和为S2，则(　　)

A．S1＝S2

B．S1＜S2

C．S1＞S2

D．无法确定

13．如图，已知菱形ABCD的边长为1.5cm，B，C两点在扇形AEF的上，求的长度及扇形ABC的面积．

参考答案X kB1.cOM

复习巩固

1．B

2．B　轴心到分针外端点的长为5cm，即半径R＝5cm，经过40min，分针转过的圆心角的度数为240°，可求得弧长是cm.

3．B

4．C

5．D

6．1

7．120°

8．π　∵△ABC为正三角形，∴∠A＝∠B＝∠C＝60°，AB＝AC＝BC＝1.∴.

根据题意可知“凸轮”的周长为三个弧长的和，即凸轮的周长.

9．解：∵，

∴∠CDA＝∠DAB，

即CD∥AB.

∴S△ACD＝S△OCD.

∴S阴影＝S扇形OCD＝

.

能力提升

10．B　由勾股定理，得AB＝＝5(cm)．xkb1.com

第一次翻滚，点A绕点B转到点A1的位置，转过的圆心角为90°，半径是线段AB的长度；第二次翻滚，点A1绕点C转到点A2的位置，转过的圆心角为90°－30°＝60°，半径是3cm，两次翻滚点A共走过的路径长是两次转过的弧长之和：(cm)．故选B.

11．A　过点O作OD⊥AB，

∵∠AOB＝120°，OA＝2，

∴∠OAD＝90°－＝180°－＝30°.

∴OD＝OA＝×2＝1，x k b 1 . c o m

.

∴AB＝2AD＝.

∴S阴影＝S扇形OAB－S△AOB＝.故选A.

12．A　S1＝π·，S2＝π·，

∵△ABC为直角三角形，

∴AC2＋BC2＝AB2.

∴(BC2＋AC2)，

即S1＝S2.

13．解：∵点B，C在上，∴AB＝AC.

∵四边形ABCD是菱形，

∴AB＝BC，即△ABC为等边三角形．∴∠BAC＝60°.

∴的长为l＝(cm)，

S扇形ABC＝lR＝××1.5＝(cm2)．

新课 标第 一 网