数学九年级上册24.1.4 圆周角精练

这是一份数学九年级上册24.1.4 圆周角精练，共10页。试卷主要包含了下列图形中的角是圆周角的是等内容，欢迎下载使用。
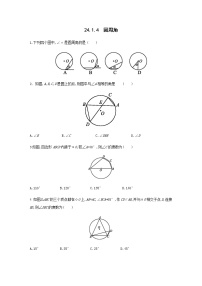
1.下列图形中的角是圆周角的是( )
2.如图,已知点A,B,C在☉O上,∠A＝72°,则∠OBC的度数是( )
A.12°B.15°
C.18°D.20°
变式：如图,点A,B,C在☉O上,OA,OB是圆的半径,连接AB,BC,AC.若∠ABO＝55°,则∠ACB的度数是 .
知识点2 圆周角定理的推论
3.如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A＝60°,AC＝2,则☉O的直径是( )
A.2B.4C.3D.23

第3题图 第4题图
4.如图,AB是☉O的直径,点C,D在☉O上,∠AOC＝70°,AD∥OC,则∠ABD＝ .
5.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E＝22.5°,AB＝2,则半径OB的长为 .
6.如图,AB是☉O的直径,弦CD⊥AB于点E,∠ACD＝30°,AE＝2,求BD的长.
知识点3 圆内接四边形的性质
7.如图,四边形ABCD为☉O的内接四边形,∠BOD＝120°,则∠BCD的大小是( )
A.120°B.100°C.80°D.60°

第7题图 第8题图
8.如图,A,B,C,D四点都在☉O上,若∠C＝100°,则∠BAD＝ ;∠BOD＝ .
9.如图,四边形ABCD内接于☉O,AC,BD为其对角线,∠ACB＝∠BAD,过点A作AE∥BC,交CD的延长线于点E.求证:EC＝AC.
10.已知半径为5的☉O中,弦AB＝52,弦AC＝5,则∠BOC的度数是( )
A.15°B.210°
C.30°或150°D.60°或90°
11.如图,A,B,C,D,E都是☉O上的点,AC＝AE,∠B＝118°,则∠D的度数为( )
A.122°B.124°
C.126°D.128°

第11题图 第12题图
12.如图,AD是☉O的直径,弦BC与弦CD的长度相同,且∠A＝60°,则∠DOC＝ .
13.如图,在△ABC中,AB＝AC＝5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD＝1,则BE的长为 .
14.如图,在☉O中,AB＝CD,∠A＝∠C,AB,CD交于点P.求证DP＝BP.
15.如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD＝BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定?若能,求出CD的长.
16.如图,四边形ABCD内接于圆,∠ABC＝60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)若AD＝2,CD＝3,求四边形ABCD的面积.
24.1.4 圆周角
知识点1 圆周角定理
1.下列图形中的角是圆周角的是(B)
2.如图,已知点A,B,C在☉O上,∠A＝72°,则∠OBC的度数是(C)
A.12°B.15°
C.18°D.20°
变式：如图,点A,B,C在☉O上,OA,OB是圆的半径,连接AB,BC,AC.若∠ABO＝55°,则∠ACB的度数是 35° .
知识点2 圆周角定理的推论
3.如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A＝60°,AC＝2,则☉O的直径是(B)
A.2B.4C.3D.23

第3题图 第4题图
4.如图,AB是☉O的直径,点C,D在☉O上,∠AOC＝70°,AD∥OC,则∠ABD＝ 20° .
5.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E＝22.5°,AB＝2,则半径OB的长为 2 .
6.如图,AB是☉O的直径,弦CD⊥AB于点E,∠ACD＝30°,AE＝2,求BD的长.
BD＝2DE＝43.
知识点3 圆内接四边形的性质
7.如图,四边形ABCD为☉O的内接四边形,∠BOD＝120°,则∠BCD的大小是(A)
A.120°B.100°C.80°D.60°

第7题图 第8题图
8.如图,A,B,C,D四点都在☉O上,若∠C＝100°,则∠BAD＝ 80° ;∠BOD＝ 160° .
9.如图,四边形ABCD内接于☉O,AC,BD为其对角线,∠ACB＝∠BAD,过点A作AE∥BC,交CD的延长线于点E.求证:EC＝AC.
证明:略
10.已知半径为5的☉O中,弦AB＝52,弦AC＝5,则∠BOC的度数是(C)
A.15°B.210°
C.30°或150°D.60°或90°
11.如图,A,B,C,D,E都是☉O上的点,AC＝AE,∠B＝118°,则∠D的度数为(B)
A.122°B.124°
C.126°D.128°

第11题图 第12题图
12.如图,AD是☉O的直径,弦BC与弦CD的长度相同,且∠A＝60°,则∠DOC＝ 60° .
13.如图,在△ABC中,AB＝AC＝5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD＝1,则BE的长为 4 .
14.如图,在☉O中,AB＝CD,∠A＝∠C,AB,CD交于点P.求证DP＝BP.
证明:略
15.如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD＝BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定?若能,求出CD的长.
解:(1)∵AB是☉O的直径,
∴∠ACB＝∠ADB＝90°.
∵AB＝10 cm,AC＝6 cm,∴BC＝8 cm.
∵AD＝BD,∴AD＝BD＝22AB＝52 cm.
(2)图中线段CD的长能确定.作AE⊥CD于点E.
∵AE⊥CD,∠ACE＝∠ABD＝45°,
∴AE＝CE＝22AC＝32 cm.
在Rt△AED中,DE＝AD2-AE2＝42 cm,
∴CD＝CE＋DE＝32＋42＝72(cm).
16.如图,四边形ABCD内接于圆,∠ABC＝60°,对角线BD平分∠ADC.
(1)求证:△ABC是等边三角形;
(2)若AD＝2,CD＝3,求四边形ABCD的面积.
解:(1)略
(2)过点A作AM⊥CD交CD延长线于点M,过点B作BN⊥AC,垂足为N,∴∠AMD＝90°.
∵∠ADC＝120°,∴∠ADM＝60°,∴∠DAM＝30°,
∴DM＝12AD＝1,AM＝AD2-DM2＝3.
∵CD＝3,∴CM＝CD＋DM＝4,
∴S△ACD＝12CD·AM＝332,
在Rt△AMC中,AC＝AM2＋CM2＝19.
∵△ABC是等边三角形,∴AB＝BC＝AC＝19,
∴BN＝32BC＝572,
∴S△ABC＝12AC·BN＝1934,
∴S四边形ABCD＝S△ACD＋S△ABC＝2534.