2022年中考数学三轮冲刺专题训练05《函数与几何图形的综合》（含答案）

专题训练(五)　[函数与几何图形的综合]

1.已知函数y=mx2-(2m-5)x+m-2的图象与x轴有两个公共点.

(1)求m的取值范围,并写出当m取范围内最大整数时函数的解析式;

(2)题(1)中求得的函数记为C1.

①当n≤x≤-1时,y的取值范围是1≤y≤-3n,求n的值;

②函数C2:y=m(x-h)2+k的图象由函数C1的图象平移得到,其顶点P落在以原点为圆心,半径为的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.

2.如图,抛物线y=x2+bx+c与x轴交于A,B两点,B点坐标为(3,0),与y轴交于点C(0,3).

(1)求抛物线的解析式;

(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.

(3)点D为抛物线对称轴上一点.当△BCD是以BC为直角边的直角三角形时,求点D的坐标.

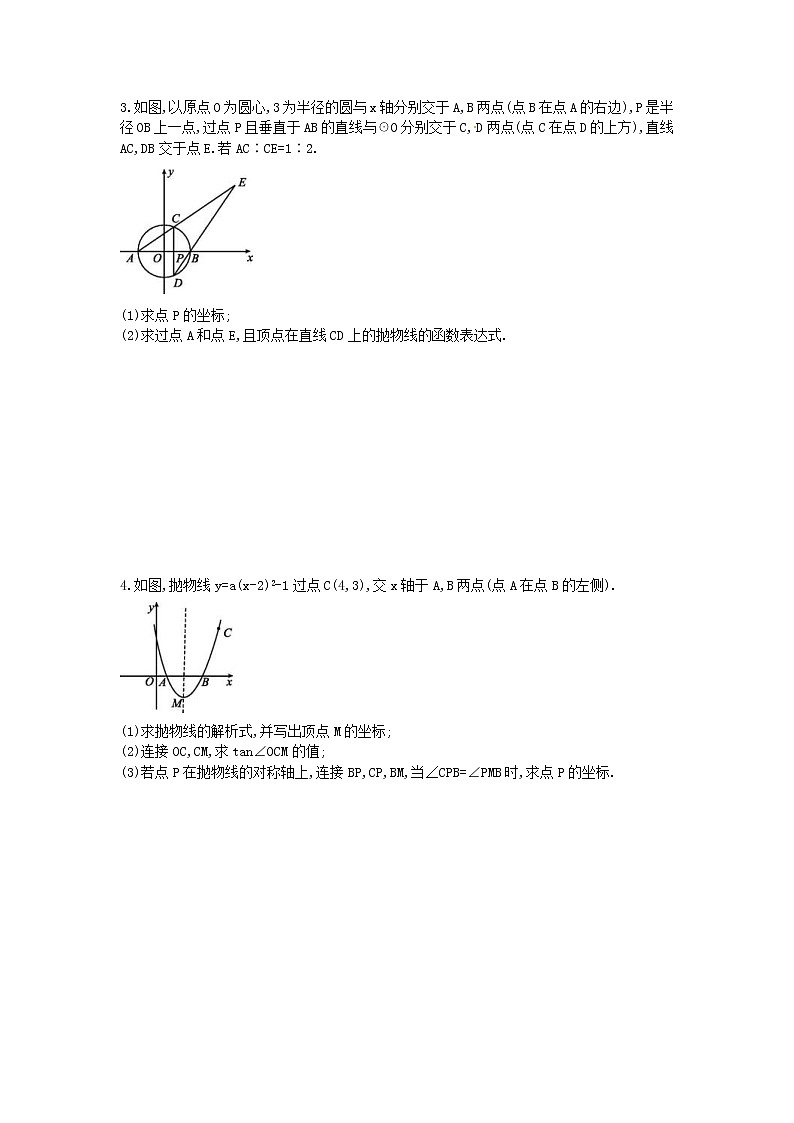
3.如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过点P且垂直于AB的直线与☉O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC∶CE=1∶2.

(1)求点P的坐标;

(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.

4.如图,抛物线y=a(x-2)2-1过点C(4,3),交x轴于A,B两点(点A在点B的左侧).

(1)求抛物线的解析式,并写出顶点M的坐标;

(2)连接OC,CM,求tan∠OCM的值;

(3)若点P在抛物线的对称轴上,连接BP,CP,BM,当∠CPB=∠PMB时,求点P的坐标.

5.如图①,在平面直角坐标系中,直线l:y=x+m与x轴,y轴分别交于点A和点B(0,-1),抛物线y=x2+bx+c经过点B,且与直线l的另一个交点为C(4,n).

(1)求n的值和抛物线的解析式.

(2)点D在抛物线上,且点D的横坐标为t(0<t<4),DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图②).若矩形DFEG的周长为p,求p与t的函数关系式及p的最大值.

(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1,点A,O,B的对应点分别是点A1,O1,B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.

6.如图,在平面直角坐标系中,抛物线y=x2-x-与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.

(1)求直线AE的解析式.

(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是线段CP上的一点,点N是线段CD上的一点,求KM+MN+NK的最小值.

(3)点G是线段CE的中点,将抛物线y=x2-x-沿x轴正方向平移得到新抛物线y',y'经过点D,y'的顶点为点F.在新抛物线y'的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.

参考答案

1.解:(1)由题意可得:

解得:m<,且m≠0.

当m=2时,函数解析式为y=2x2+x.

(2)①函数y=2x2+x图象开口向上,对称轴为直线x=-,

∴当x<-时,y随x的增大而减小.

∵当n≤x≤-1时,y的取值范围是1≤y≤-3n,

∴2n2+n=-3n.

∴n=-2或n=0(舍去).

∴n=-2.

②∵y=2x2+x=2x+2-,

∴函数C1的图象顶点M的坐标为-,-.

由图形可知当P为射线MO与圆的交点时,距离最大.

∵点P在直线OM上,由O(0,0),M-,-可求得直线的解析式为y=x.

设P(a,b),则有a=2b.

根据勾股定理可得PO2=(2b)2+b2=()2,解得b=1(负值已舍).

∴a=2.

∴PM最大时函数C2的解析式为y=2(x-2)2+1.

2.解:(1)由题意得解得

∴抛物线的解析式为y=x2-4x+3.

(2)方法1(代数法):如图①,过点P作PG∥CF交CB于点G,

由题意知∠BCO=∠CFE=45°,F(0,m),C(0,3),

∴△CFE和△GPE均为等腰直角三角形,

∴EF=CF=(3-m),PE=PG.

又易知直线BC的解析式为y=-x+3.

设xP=t(1<t<3),则PE=PG=(-t+3-t-m)=(-m-2t+3).

又∵t2-4t+3=t+m,∴m=t2-5t+3.

∴PE+EF=(3-m)+(-m-2t+3)=(-2t-2m+6)=-(t+m-3)=-(t2-4t)=-(t-2)2+4,

∴当t=2时,PE+EF取最大值4.

方法2:(几何法)如图②,由题易知直线BC的解析式为y=-x+3,OC=OB=3,

∴∠OCB=45°.

同理可知∠OFE=45°,

∴△CEF为等腰直角三角形.

以BC为对称轴将△FCE对称得到△F'CE,作PH⊥CF'于点H

则PE+EF=PF'=PH.

又PH=yC-yP=3-yP.

∴当yP最小时,PE+EF取最大值.

∵抛物线的顶点坐标为(2,-1),

∴当yP=-1时,(PE+EF)max=×(3+1)=4.

(3)由(1)知对称轴为直线x=2,设D(2,n),如图③.

当△BCD是以BC为直角边的直角三角形,且D在BC上方D1位置时,

由勾股定理得C+BC2=B,

即(2-0)2+(n-3)2+(3)2=(3-2)2+(0-n)2,解得n=5;

当△BCD是以BC为直角边的直角三角形,且D在BC下方D2位置时,

由勾股定理得B+BC2=C,

即(2-3)2+(n-0)2+(3)2=(2-0)2+(n-3)2,解得n=-1.

∴当△BCD是以BC为直角边的直角三角形时,D点坐标为(2,5)或(2,-1).

3.解:(1)过点E作EF⊥x轴于点F,

∵CD⊥AB,

∴CD∥EF,PC=PD.

∴△ACP∽△AEF,

△BPD∽△BFE.

∵AC∶CE=1∶2,

∴AC∶AE=1∶3.

∴==,==.∴AF=3AP,BF=3PB.∵AF-BF=AB.

∴3AP-3PB=AB.

又∵☉O的半径为3,设P(m,0),

∴3(3+m)-3(3-m)=6,∴m=1.∴P(1,0).

(2)∵P(1,0),∴OP=1,∵A(-3,0).

∴OA=3,∴AP=4,BP=2.∴AF=12.

连接BC.∵AB是直径,∴∠ACB=90°.

∵CD⊥AB,∴△ACP∽△CBP,

∴=.

∴CP2=AP·BP=4×2=8.

∴CP=2(负值已舍).∴EF=3CP=6.

∴E(9,6).

∵抛物线的顶点在直线CD上,

∴CD是抛物线的对称轴,

∴抛物线过点(5,0).

设抛物线的函数表达式为y=ax2+bx+c.

根据题意得

解得

∴抛物线的函数表达式为y=x2-x-.

4.解:(1)由抛物线y=a(x-2)2-1过点C(4,3),

得3=a(4-2)2-1,解得a=1,

∴抛物线的解析式为y=(x-2)2-1,顶点M的坐标为(2,-1).

(2)如图,连接OM,

∵OC2=32+42=25,OM2=22+12=5,CM2=22+42=20,

∴CM2+OM2=OC2,

∴∠OMC=90°.

OM=,CM=2,tan∠OCM===.

(3)如图,过C作CN垂直于对称轴,垂足N在对称轴上,取一点E,使EN=CN=2,连接CE,EM=6.

当y=0时,(x-2)2-1=0,解得x1=1,x2=3,∴A(1,0),B(3,0).

∵CN=EN,∴∠CEP=∠PMB=∠CPB=45°,

∵∠EPB=∠EPC+∠CPB=∠PMB+∠PBM,

∴∠EPC=∠PBM,∴△CEP∽△PMB,

∴=,易知MB=,CE=2,

∴=,解得PM=3±,

∴P点坐标为(2,2+)或(2,2-).

5.解:(1)∵直线l:y=x+m经过点B(0,-1),

∴m=-1,

∴直线l的解析式为y=x-1.

∵直线l:y=x-1经过点C(4,n),

∴n=×4-1=2.

∵抛物线y=x2+bx+c经过点C(4,2)和点B(0,-1),

∴

解得

∴抛物线的解析式为y=x2-x-1.

(2)令y=0,则x-1=0,

解得x=,

∴点A的坐标为,0,

∴OA=.

在Rt△OAB中,OB=1,

∴AB===.

∵DE∥y轴,

∴∠ABO=∠DEF,

在矩形DFEG中,EF=DE·cos∠DEF=DE·=DE,

DF=DE·sin∠DEF=DE·=DE,

∴p=2(DF+EF)=2×+DE=DE,

∵点D的横坐标为t(0<t<4),

∴Dt,t2-t-1,Et,t-1,

∴DE=t-1-t2-t-1=-t2+2t,

∴p=×-t2+2t=-t2+t,

∴p=-(t-2)2+,且-<0,

∴当t=2时,p有最大值.

(3)∵△AOB绕点M沿逆时针方向旋转90°,

∴A1O1∥y轴,B1O1∥x轴.设点A1的横坐标为x,

如图①,点O1,B1在抛物线上时,点O1的横坐标为x,点B1的横坐标为x+1,

∴x2-x-1=(x+1)2-(x+1)-1,

解得x=.

如图②,点A1,B1在抛物线上时,点B1的横坐标为x+1,点A1的纵坐标比点B1的纵坐标大,

∴x2-x-1=(x+1)2-(x+1)-1+,

解得x=-.

综上所述,点A1的横坐标为或-.

6.解:(1)令y=0,得x2-x-=0,

解得x1=-1,x2=3,

∴点A(-1,0),B(3,0).

∵点E(4,n)在抛物线上,

∴n=×42-×4-=,

即点E,

设直线AE的解析式为y=kx+b,

则,解得

∴直线AE的解析式为y=x+.

(2)令y=x2-x-中x=0,得y=-,

∴C(0,-).由(1)得点E,

∴直线CE的解析式为y=x-.

过点P作PH∥y轴,交CE于点H,如图①,

设点Pt,t2-t-,则Ht,t-,

∴PH=t--=-t2+t,

∴S△PCE=S△PHC+S△PHE=·PH·

=××4

=-t2+t

=-(t2-4t)

=-(t-2)2+.

∵-<0,

∴当t=2时,S△PCE最大,此时点P(2,-).

∵C(0,-),

∴PC∥x轴.

∵B(3,0),K为BC的中点,

∴K,-.

如图②,作点K关于CP,CD的对称点K1,K2,连接K1K2,分别交CP,CD于点M,N.

此时KM+MN+NK最小,易知K1,-.

∵OC=,OB=3,OD=1,

∴∠OCB=60°,∠OCD=30°,

∴CD平分∠OCB,

∴点K2在y轴上.

∵CK=OC=,

∴点K2与原点O重合,

∴KM+MN+NK=K1M+MN+NO=OK1==3,

∴KM+MN+NK的最小值为3.

(3)存在.如图③,点Q的坐标分别为Q1(3,2),Q23,,Q33,-,

Q43,.