小学数学西师大版六年级下册图形与几何复习ppt课件

这是一份小学数学西师大版六年级下册图形与几何复习ppt课件，共47页。PPT课件主要包含了长方体和正方体的认识，长方体的认识，有8个顶点，正方体的认识，圆柱和圆锥的认识，圆柱的认识，圆锥的认识，长方体的表面积，长×高，长×宽等内容，欢迎下载使用。

1.通过复习,进一步认识长方体、正方体、圆柱、圆锥等图形,掌握它们的特征,把握有关图形之间的相互联系。2.掌握所学的立体图形的表面积和体积的含义,会计算它们的表面积和体积,并解决简单的实际问题。3.在解决问题的过程中,体会知识与生活之间的联系,增强应用数学的意识,体会数学的魅力。
【重点】 能正确计算常见立体图形的表面积和体积,并解决一些 简单的实际问题。【难点】 感受数学知识和方法的内在联系,体会转化、 类比等数学思想方法,发展初步推理能力。
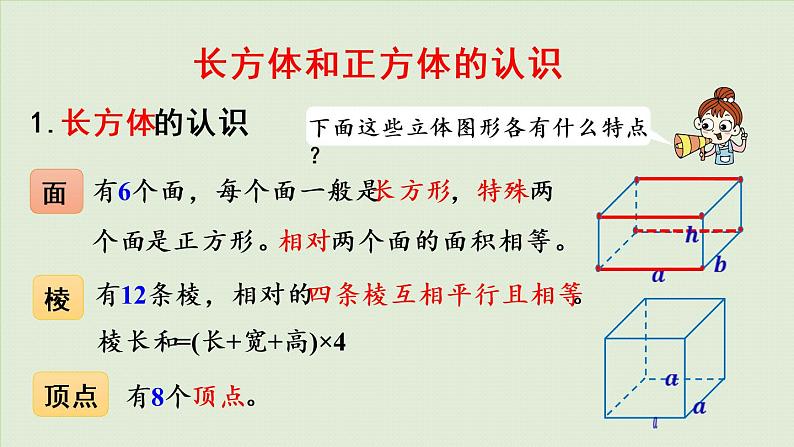
有6个面，每个面一般是长方形，特殊两个面是正方形。相对两个面的面积相等。
有12条棱，相对的四条棱互相平行且相等。
棱长和=(长+宽+高)×4
有6个面，每个面都是正方形，每个面面积都相等。
有12条棱，每条棱长度都相等。
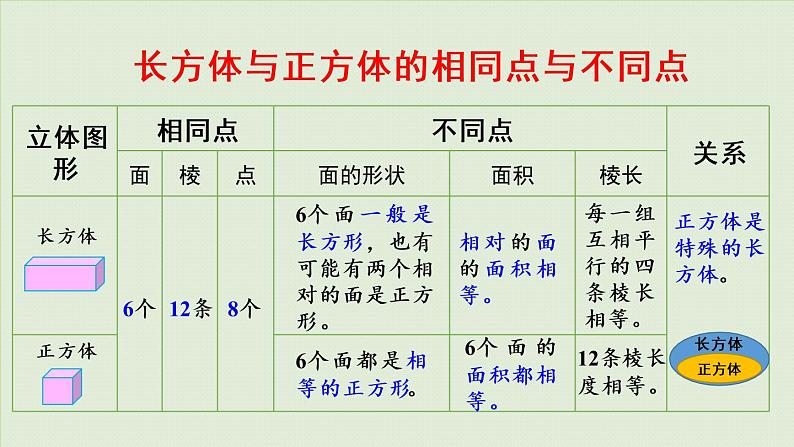
长方体与正方体的相同点与不同点
6个面一般是长方形，也有可能有两个相对的面是正方形。
6个面都是相等的正方形。
每一组互相平行的四条棱长相等。
正方体是特殊的长方体。
三个面，上、下两个圆是底面，侧面是一个曲面。
两个面，底面是一个圆，侧面是一个曲面。
3.圆柱和圆锥之间的关系
圆柱与圆锥可以各由什么平面图形旋转而成？
圆柱可以由一个长方形绕着它的一条边旋转360°（或由矩形绕着它的一条对称轴旋转180°）得到。
圆锥可以由一个直角三角形绕着它的一条直角边旋转360°得到。
长方体和正方体的表面积
长方体相对面的面积相等。
表面积=(长×宽+长×高+宽×高)×2
正方体6个面都是相等的正方形。
表面积=棱长×棱长×6
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体和正方体体积的统一公式=底面积×高
底面积=底面半径²×圆周率×2
表面积=底面积+侧面积
S表=2πr(r+h)
求需要多少硬纸片，就是求长方体的表面积。
1.要在下图的六个面上贴上硬纸片，至少需要多少平方 厘米硬纸片？
(6×3＋3×3＋6×3)×2= 45×2= 90(cm²)
答：至少需要90 cm²硬纸片。
2.一个无盖玻璃鱼缸的形状是正方体，棱长3 dm。制作 这个 鱼缸时至少需要多少平方分米玻璃？
这个正方体5个面的面积之和是棱长×棱长×5。
3×3×5=45(平方分米) 答：制作这个鱼缸时至少需要45平方分米玻璃。
3. 一顶圆柱形厨师帽，高30 cm，帽顶直径20 cm，做这 样一顶帽子至少需要用多少平方厘米的面料？（得数 保留整十数）
这个帽子是什么样的，它由哪几面组成？
“没有底”的帽子的展开图，它是由一个底面和一个侧面组成。
帽子的侧面积：3.14×20×30=1884（平方厘米）
帽顶的面积：3.14×（20÷2）2 =314（平方厘米）
需要面料面积：1884+314=2198 ≈ 2200（平方厘米）
答：做这样一顶帽子至少需要用2200平方厘米的面料。
4.一个正方体的棱长总和是108厘米，它的体积是多少？
正方体棱长总和=棱长×12
108÷12=9(厘米)
9×9×9=729(立方厘米)
答：它的体积是729立方厘米。
5.一根长方体木料，长5 m，横截面的面积是0.06 m2。 这根木料的体积是多少？
长方体体积=底面积×高
0.06×5＝0.3（m3）
答：这根木料的体积是0.3m3。
6.工地上有一堆沙子，近似于一个圆锥（如下图）。这 堆沙子的体积大约是多少？如果每立方米沙子重1.5 t， 那么这堆沙子大约重多少吨？
沙堆的底面积： 3.14 ×（4÷2）2 =12.56（m2）
沙堆的重量：6.28×1.5=9.42（t）
答：这堆沙子大约6.28 m3。
答：这堆沙子大约重9.42 t。
不同位置观察一个立体图形，所看到的形状一般不同。
8.这3个图形，从哪面看到的图形相同？从哪面看到的图形不同？
不同形状的立体图形从同一方向进行观察，所看到的形状可能不同，也可能相同。
8.按从不同方向看到的图形摆出几何体。
搭几何体时，先从一个方向确定基本形状，然后从另外两面确定层数和每层的个数。
1. 判断下列说法是否正确。
（教材第100页练习二十三第1题）
（1）用3个同样大小的正方体拼成一个长方体，长方 体的表面积是正方体的3倍。 （2）圆柱底面的直径是5 cm，高也是5 cm，它的侧面 展开图是一个正方形。 （3）把一个体积是15 cm3的圆柱削成一个体积最大的 圆锥，圆锥的体积是5 cm3。
2.下面第1排中的平面图形绕红线旋转1周能形成第2排的 哪个立体图形？（连线）
（教材第100页练习二十三第3题）
3.计算下面各图的表面积和体积。（图中单位：cm）
（教材第100页练习二十三第4题）
表面积：（15×10+8×10+15×8）×2=700（cm2）
体积：15×10×8=1200（cm3）
表面积：6×10×10=600（cm2）
体积：10×10×10=1000（cm3）
表面积： 2×3.14×42+3.14×8×12=401.92（cm2）
体积：3.14×42×12=602.88（cm3）
4.下面这个容器一共能装多少毫升水？（容器壁的厚度 忽略不计。）
（教材第101页练习二十三第5题）
8×5×2+3.14×(4÷2)2×3=117.68（dm3）=117680（mL）
答：这个容器能装117680毫升水。
5. 一台长方体形冰箱长0.6 m，宽0.5 m，高1.8 m。（1）做这台冰箱的包装盒至少需要纸板多少平方米？（2）这台冰箱占地面积是多少平方米？
（教材第101页练习二十三第6题）
（1）（0.6×0.5+0.6×1.8+0.5×1.8）×2=4.56（m2） 答：做这台冰箱的包装盒至少需要纸板4.56平方米。
（2）0.6×0.5=0.3（m2） 答：这台冰箱占地面积是0.3平方米。
6.一条水渠长800 m，横截面如下图。
（教材第101页练习二十三第7题）
（1）水渠的横截面积是多少平方米？
4×2.5=10（平方米）
答：水渠的横截面积是10平方米。
（2）水渠水深2 m，水在水渠中每分流动20 m，该水渠 每时的水流量是多少立方米？
2×4×20×60=9600（立方米）
答：该水渠每时的水流量是9600立方米。
7.学校修建花园需要40吨沙，这堆沙够用吗？（每立方 米沙重1.8 吨。）
（教材第101页练习二十三第8题）
12.56÷3.14÷2=2（米）
5.024×1.8=9.0432（吨）
8.把两个完全一样的小长方体木块粘成一个大长方体， 这个大长方体的表面积比原来两个小长方体的表面 积的和减少50 cm²。如果拼成的大长方体长20 cm， 那么一个小长方体的体积是多少立方厘米？
减少了两个侧面的面积。
一个侧面的面积：50÷2=25(cm²)
小长方体的高：20÷2=10(cm)
(50÷2)×(20÷2)=250(cm³)答：一个小长方体的体积是250 cm³。
8.把两个完全一样的小长方体木块粘成一个大长方体， 这个大长方体的表面积比原来两个小长方体的表面 积的和减少50 cm²。如果拼成的大长方体长20 cm， 那么一个小长方体的体积是多少立方厘米？