人教版八年级下册17.1 勾股定理习题ppt课件

这是一份人教版八年级下册17.1 勾股定理习题ppt课件，共18页。PPT课件主要包含了答案呈现，习题链接等内容，欢迎下载使用。

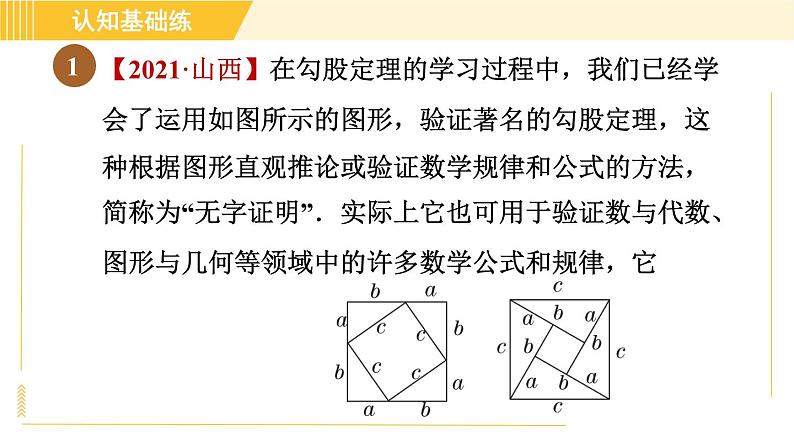
【2021·山西】在勾股定理的学习过程中，我们已经学会了运用如图所示的图形，验证著名的勾股定理，这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”．实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律，它
体现的数学思想是(　　)A ．统计思想 B． 分类思想C． 数形结合思想 D． 函数思想
【教材P30阅读与思考改编】历史上对勾股定理的一种验证方法采用了如图所示的图形，其中两个全等直角三角形的两边AE，EB在一条直线上．验证过程中用到的面积相等的关系式是(　　)A． S△EDA＝S△CEBB． S△EDA＋S△CEB＝S△CDEC． S四边形CDAE＝S四边形CDEBD． S△EDA＋S△CDE＋S△CEB＝S四边形ABCD
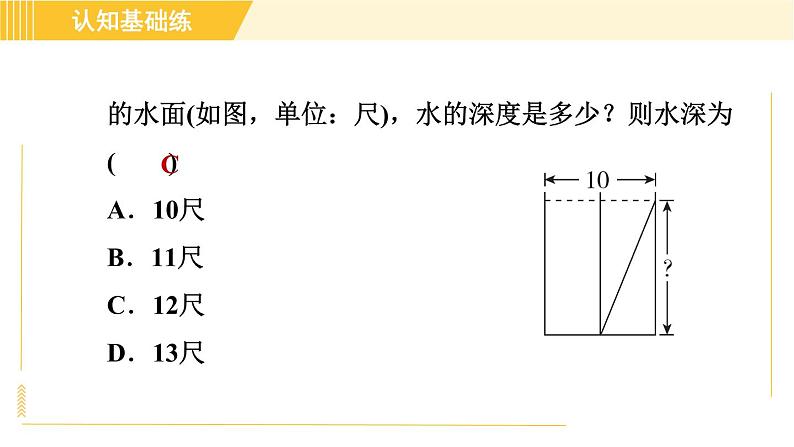
【教材P29习题T10改编】【2021·襄阳】我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭(jiā)生其中，出水一尺，引葭赴岸，适与岸齐，问水深几何．”(丈、尺是长度单位，1丈＝10尺)其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边
的水面(如图，单位：尺)，水的深度是多少？则水深为(　　)A．10尺　 B．11尺　 C．12尺　 D．13尺
【点拨】设水深为h尺，则芦苇长为(h＋1)尺．根据勾股定理，得(h＋1)2－h2＝(10÷2)2，解得h＝12.所以水深为12尺．
已知直角三角形的两边长求第三边长时，如果题中没有说明这两条边长是直角边长还是斜边长，则要分两种情况讨论．
【教材P23图17.1­ 5改编】现用4个全等的直角三角形拼成如图所示的“赵爽弦图”．在Rt△ABC中，∠ACB＝90°，若AC＝b，BC＝a，AB＝c，请你利用这个图形解决下列问题： (1)求证：a2＋b2＝c2；
(2)如果大正方形的面积是6，小正方形的面积是2，求(a＋b)2的值.
在△ABC中，BC＝a，AC＝b，AB＝c，若∠C为直角，则由勾股定理可得a2＋b2＝c2. (1)若∠C为锐角，求证：a2＋b2＞c2；
证明：过点A作AD⊥BC于点D，如图①所示，则BD＝BC－CD＝a－CD.在Rt△ABD中，AB2－BD2＝AD2；在Rt△ACD中，AC2－CD2＝AD2，∴AB2－BD2＝AC2－CD2，即c2－(a－CD)2＝b2－CD2，整理，得a2＋b2＝c2＋2a·CD.∵a＞0，CD＞0，∴a2＋b2＞c2.
(2)若∠C为钝角，试猜想a2＋b2与c2之间的数量关系，并说明理由.
解：a2＋b2＜c2.理由如下：过点A作AD⊥BC交BC的延长线于点D，如图②所示，则BD＝BC＋CD＝a＋CD.在Rt△ABD中，AD2＝AB2－BD2；在Rt△ACD中，AD2＝AC2－CD2，