人教版九年级上册第二十二章 二次函数综合与测试当堂检测题

这是一份人教版九年级上册第二十二章 二次函数综合与测试当堂检测题，共21页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

 2021-2022学年度九年级数学知识滚动检测试卷
(包含内容：第22章)

一、单项选择题（每题3分，共30分）
1．把二次函数y＝x2﹣4x﹣3化成y＝a（x﹣h）2+k的形式，正确的是（　　）
A．y＝（x﹣2）2﹣1 B．y＝（x﹣2）2+1 C．y＝（x﹣2）2﹣7 D．y＝（x+2）2+1
2．如果函数y=m−2xm2−2+2x−7是二次函数，则m的取值范围是（　　）
A．m＝±2 B．m＝2
C．m＝﹣2 D．m为全体实数
3．二次函数y＝a（x+m）2+k的图象如图所示，下列四个选项中，正确的是（　　）

A．m＜0，k＜0 B．m＜0，k＞0 C．m＞0，k＞0 D．m＞0，k＞0
4．直线y＝bx+c与抛物线y＝ax2+bx+c（a＞0）在同一坐标系中大致图象可能是（　　）
A．BC． D．
5．关于二次函数y＝14x2﹣6x+a+27，下列说法错误的是（　　）
A．若将图象向上平移10个单位，再向左平移2个单位后过点（4，5），则a＝﹣5
B．当x＝12时，y有最小值a﹣9
C．x＝2对应的函数值比最小值大7
D．当a＜0时，图象与x轴有两个不同的交点
6．已知点P（m，n）在抛物线y＝a（x﹣5）2+9（a≠0）上，当3＜m＜4时，总有n＞1，当7＜m＜8时，总有n＜1，则a的值为（　　）
A．1 B．﹣1 C．2 D．﹣2
7．抛物线y=−x2+4x−4与坐标轴的交点个数为（ ）
A．0 B．1 C．2 D．3
8．将抛物线C1:y=x2−2x+3向左平移1个单位长度，得到抛物线C2，抛物线C2与抛物线关于x轴对称，则抛物线的解析式为（ ）
A．y=−x2−2 B．y=−x2+2 C．y=x2−2 D．y=x2+2
9．若抛物线y=ax2+bx+c(a>0)经过第四象限的点1,−1），则关于x的方程ax2+bx+c=0的根的情况是（ ）
A．有两个大于1的不相等实数根 B．有两个小于1的不相等实数根
C．有一个大于1另一个小于1的实数根 D．没有实数根
10．抛物线y=ax2+bx+c的对称轴是直线x=−1，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：
①ab>0且c<0；
②；
③8a+c>0；
④c=3a−3b；
⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1、x2，则x1+x2+x1⋅x2=−5.其中正确的个数有( )

A．5个 B．4个 C．3个 D．2个
二、填空题（每小题3分，共18分）
11. 抛物线y＝ax2+bx+c的部分图象如图，则当y＞3时，x的取值范围是　　．

12. 某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100﹣x）件，获利y元，当获利最大时，售价x＝　　元．
13. .若抛物线的顶点坐标为（2，9），且它在x轴截得的线段长为6，则该抛物线的表达式为　　　　　．

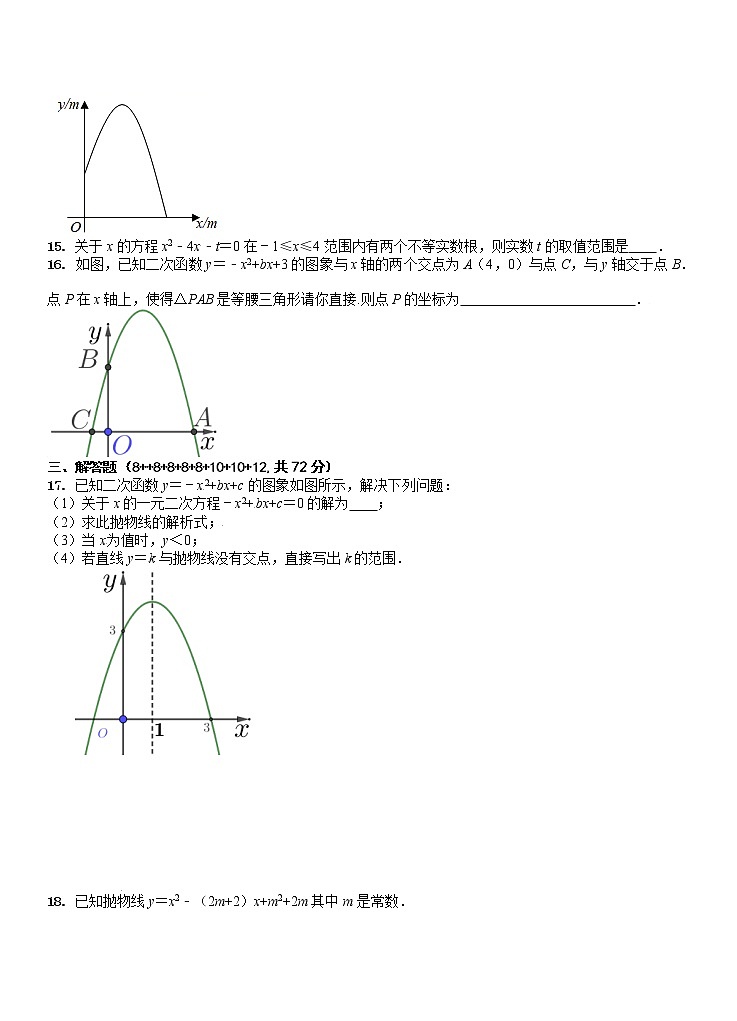
14. 从喷水池喷头喷出的水珠，在空中形成一条抛物线，如图所示，在抛物线各个位置上，水珠的竖直高度y（单位：m）与它距离喷头的水平距离x（单位：m）之间满足函数关系式，喷出水珠的最大高度是______m．

15. 关于x的方程x2﹣4x﹣t＝0在﹣1≤x≤4范围内有两个不等实数根，则实数t的取值范围是　　．
16. 如图，已知二次函数y＝﹣x2+bx+3的图象与x轴的两个交点为A（4，0）与点C，与y轴交于点B．
点P在x轴上，使得△PAB是等腰三角形请你直接.则点P的坐标为 ．

三、解答题（8++8+8+8+8+10+10+12,共72分）
17. 已知二次函数y＝﹣x2+bx+c的图象如图所示，解决下列问题：
（1）关于x的一元二次方程﹣x2+bx+c＝0的解为　　；
（2）求此抛物线的解析式；
（3）当x为值时，y＜0；
（4）若直线y＝k与抛物线没有交点，直接写出k的范围．









18. 已知抛物线y＝x2﹣（2m+2）x+m2+2m其中m是常数．
（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点；
（2）若该抛物线的对称轴为直线x＝4．
①求该抛物线的函数解析式；
②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点．









19. 在平面直角坐标系xOy中，二次函数y＝ax2+2x﹣3a（a≠0）交x轴于A、B两点（点A在点B的左侧），且抛物线的对称轴为直线x＝﹣1．
（1）求此抛物线的解析式及A、B两点坐标；
（2）若抛物线交y轴于点C，顶点为D，求四边形ABCD的面积．














20. 有一家网红私人定制蛋糕店，她家的蛋糕经常供不应求，但每日最多只能做40只蛋糕，且每日做好的蛋糕全部订售一空．已知做x只蛋糕的成本为R元，售价为每只P元，且R、P与x的关系式为R＝500+30x，P＝170﹣2x，设她家每日获得的利润为y元．
（1）销售x只蛋糕的总售价为　　元（用含x的代数式表示），并求y与x的函数关系式；
（2）当每日做多少只蛋糕时，每日获得的利润为1500元？
（3）当每日做多少只蛋糕时，每日所获得的利润最大？最大日利润是多少元？












21. 已知，如图，抛物线y＝﹣x2+bx+c经过直线y＝﹣x+3与坐标轴的两个交点A，B．此抛物线与x轴的另一个交点为C．抛物线的顶点为D．
（1）求此抛物线的解析式．
（2）若点M为抛物线上一动点，是否存在点M．使△ACM与△ABC的面积相等？若存在，求点M的坐标；若不存在，请说明理由．










22. 某客商准备购一批特色商品，经调查，用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍，一件A型商品的进价比一件B型商品的进价多10元．
（1）求一件A，B型商品的进价分别为多少元？
（2）若该客商购进A，B型商品共250件进行试销，其中A型商品的件数不大于B型的件数，且不小于20件．已知A型商品的售价为240元/件，B型商品的售价为220元/件，且全部售出．设购进A型商品m件，
①写出m的取值范围　　；
②求出商场销售这批商品的最大利润，并求出此时的进货方案．
（3）若m的范围与（2）保持一致，但是A型商品的售价与A型商品销量之间的关系如下表所示：
A型商品的售价
240
230
220
210
200
……
A型商品的销量
0
5
10
15
20
……
B型商品的售价降为210元/件，且全部售出．设购进A型商品m件，求出这批商品的最大利润，并求出此时的进货方案．








23. 如图，已知二次函数图象的顶点坐标为C（1，0），直线y＝x+m的图象与该二次函数的图象交于A、B两点，其中A点坐标为（3，4），B点在y轴上．
（1）求m的值及这个二次函数的解析式；
（2）若P是线段AB下方抛物线上一动点，当△ABP面积最大时，求P点坐标以及△ABP面积最大值；（3）若D为直线AB与这个二次函数图象对称轴的交点，Q为线段AB之间的一个动点，过Q作x轴的垂线，与这个二次函数图象交于点E，问是否存在这样的点Q，使得四边形DCEQ为平行四边形，若存在，请求出Q点的坐标；若不存在，请说明理由．

























24. 如图，已知二次函数的图象经过点A（4，4），B（5，0）和原点O，P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为D（m，0），并与直线OA相较于点C．
（1）求出二次函数的解析式；
（2）当点P在直线OA的上方时，求线段PC的最大值；
（3）当点P在直线OA的上方时，是否存在一点P，使射线OP平分∠AOy，若存在，请求出P点坐标；若不存在．请说明理由；
（4）当m＞0时，探索是否存在点P，使得△PCO为等腰三角形，若存在，求出P点的坐标；若不存在，请说明理由．



























答案：
一、单项选择题（每题3分，共30分）
1．把二次函数y＝x2﹣4x﹣3化成y＝a（x﹣h）2+k的形式，正确的是（　　）
A．y＝（x﹣2）2﹣1 B．y＝（x﹣2）2+1 C．y＝（x﹣2）2﹣7 D．y＝（x+2）2+1
【答案】 C
2．如果函数y=m−2xm2−2+2x−7是二次函数，则m的取值范围是（　　）
A．m＝±2 B．m＝2
C．m＝﹣2 D．m为全体实数
【答案】 C
3．二次函数y＝a（x+m）2+k的图象如图所示，下列四个选项中，正确的是（　　）

A．m＜0，k＜0 B．m＜0，k＞0 C．m＞0，k＞0 D．m＞0，k＞0
【答案】A
4．直线y＝bx+c与抛物线y＝ax2+bx+c（a＞0）在同一坐标系中大致图象可能是（　　）
A．BC． D．
【答案】B
5．关于二次函数y＝14x2﹣6x+a+27，下列说法错误的是（　　）
A．若将图象向上平移10个单位，再向左平移2个单位后过点（4，5），则a＝﹣5
B．当x＝12时，y有最小值a﹣9
C．x＝2对应的函数值比最小值大7
D．当a＜0时，图象与x轴有两个不同的交点
【答案】C
6．已知点P（m，n）在抛物线y＝a（x﹣5）2+9（a≠0）上，当3＜m＜4时，总有n＞1，当7＜m＜8时，总有n＜1，则a的值为（　　）
A．1 B．﹣1 C．2 D．﹣2
【答案】D
【解答】解：∵抛物线y＝a（x﹣5）2+9（a≠0），
∴抛物线的顶点为（5，9），
∵当7＜m＜8时，总有n＜1，
∴a不可能大于0，
则a＜0，
∴x＜5时，y随x的增大而增大，x＞5时，y随x的增大而减小，
∵当3＜m＜4时，总有n＞1，当7＜m＜8时，总有n＜1，且x＝3与x＝7对称，
∴m＝3时，n≤1，m＝7时，n≥1，
∴4a+9≤14a+9≥1，
∴4a+9＝1，
∴a＝﹣2，
故选：D．
7．抛物线y=−x2+4x−4与坐标轴的交点个数为（ ）
A．0 B．1 C．2 D．3
【答案】C
8．将抛物线C1:y=x2−2x+3向左平移1个单位长度，得到抛物线C2，抛物线C2与抛物线关于x轴对称，则抛物线的解析式为（ ）
A．y=−x2−2 B．y=−x2+2 C．y=x2−2 D．y=x2+2
【答案】A
【分析】
利用平移的规律:左加右减，上加下减.并用规律求函数解析式C2，再因为关于x轴对称的两个抛物线，自变量x的取值相同，函数值y互为相反数，由此可直接得出抛物线的解析式．
【详解】
解：抛物线C1:y=x2−2x+3向左平移1个单位长度，得到抛物线C2：y=x+12−2x+1+3，即抛物线C2：y=x2+2;
由于抛物线C2与抛物线关于x轴对称，则抛物线的解析式为：y=−x2−2.
故选：A．
9．若抛物线y=ax2+bx+c(a>0)经过第四象限的点1,−1），则关于x的方程ax2+bx+c=0的根的情况是（ ）
A．有两个大于1的不相等实数根 B．有两个小于1的不相等实数根
C．有一个大于1另一个小于1的实数根 D．没有实数根
【答案】C
【分析】
根据抛物线的图像进行判断即可．
【详解】
∵a>0，
∴抛物线开口向上，
∵抛物线经过第四象限的点（1，-1）
∴方程ax2+bx+c=0有两个不相等的实数根，一个大于1另一个小于1，
故选：C．
10．抛物线y=ax2+bx+c的对称轴是直线x=−1，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：
①ab>0且c<0；
②；
③8a+c>0；
④c=3a−3b；
⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1、x2，则x1+x2+x1⋅x2=−5.其中正确的个数有( )

A．5个 B．4个 C．3个 D．2个
【答案】C
【详解】
∵对称轴在y轴左侧，图象与y轴交于y轴正半轴，
∴ab>0，c>0，故①错误，
∵图象过点（1，0），对称轴为x=-1，
∴图象与x轴的另一个交点为（-3，0），
∵抛物线的开口向下，
∴a<0，
∴x=-2时，4a-b+c>0，故②正确，
∵对称轴x=−b2a=-1，
∴b=2a，
∵x=1时，a+b+c=0，
∴3a+c=0，
∴8a+c=5a<0，故③错误，
∵3a+c=0，
∴c=-3a，
∴3a-3b=3a-3×2a=-3a=c，故④正确，
ax2+bx+c=2x+2，
整理得：ax2+(b-2)x+c-2=0，
∵直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1、x2，
∴x1+x2+x1⋅x2=−b−2a+c−2a=−2a+2+(−3a)−2a=-5，故⑤正确，
综上所述：正确的结论为②④⑤，共3个.
二、填空题（每小题3分，共18分）
11. 抛物线y＝ax2+bx+c的部分图象如图，则当y＞3时，x的取值范围是　　．

【答案】0＜x＜2
12. 某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100﹣x）件，获利y元，当获利最大时，售价x＝　　元．
【答案】65
13. .若抛物线的顶点坐标为（2，9），且它在x轴截得的线段长为6，则该抛物线的表达式为　　　　　．
【答案】y=-（x-2）2+9
【解答】解：∵抛物线的顶点坐标为（2，9），
∴抛物线的对称轴为直线x＝2，
∵抛物线在x轴截得的线段长为6，
∴抛物线与x轴的交点为（﹣1，0），（5，0），
设此抛物线的解析式为：y＝a（x﹣2）2+9，
代入（5，0）得，9a+9＝0，
解得a＝﹣1，
∴抛物线的表达式为y＝﹣（x﹣2）2+9，
故答案为y＝﹣（x﹣2）2+9．
14. 从喷水池喷头喷出的水珠，在空中形成一条抛物线，如图所示，在抛物线各个位置上，水珠的竖直高度y（单位：m）与它距离喷头的水平距离x（单位：m）之间满足函数关系式，喷出水珠的最大高度是______m．

【答案】3
【分析】
把二次函数化为顶点式，进而即可求解．
【详解】
解：∵y=−2x2+4x+1=−2(x−1)2+3，
∴当x=1时， y最大值=3，
故答案是：3．
15. 关于x的方程x2﹣4x﹣t＝0在﹣1≤x≤4范围内有两个不等实数根，则实数t的取值范围是　　．
【答案】-4＜t≤0
【分析】设y1＝x2﹣4x，将一元二次方程x2﹣4x﹣t＝0的实数根可以看做y1＝x2﹣4x与函数y2＝t的有交点，再由﹣1≤x≤4的范围确定y的取值范围即可求解．
【解答】解：设y1＝x2﹣4x，
∵y1＝x2﹣4x的对称轴为直线x＝2，
∴一元二次方程x2﹣4x﹣t＝0的实数根可以看作y1＝x2﹣4x与函数y2＝t的交点，
∵方程在﹣1≤x≤4的范围内有实数根，
当x＝﹣1时，y1＝5；
当x＝4时，y1＝0；
函数y1＝x2﹣4x在x＝2时有最小值﹣4；
∴当﹣4＜t≤0时，y1＝x2﹣4x与函数y2＝t有两个交点，即方程x2﹣4x﹣t＝0在﹣1≤x≤4范围内有两个不等实数根；
故答案为：﹣4＜t≤0．
16. 如图，已知二次函数y＝﹣x2+bx+3的图象与x轴的两个交点为A（4，0）与点C，与y轴交于点B．
点P在x轴上，使得△PAB是等腰三角形请你直接.则点P的坐标为 ．

【解答】解：（1）将点A的坐标代入抛物线表达式得：0＝﹣16+4b+3，解得b＝134，
故抛物线的表达式为y＝﹣x2+134x+3，
令x＝0，则y＝3，故点B的坐标为（0，3）；
令y＝﹣x2+134x+3＝0，解得x＝4或﹣34，
设点P的坐标为（x，0），
由题意得：AB2＝42+32＝25，AP2＝（x﹣4）2，BP2＝x2+9，
当AB＝AP时，则25＝（x﹣4）2，解得x＝9或﹣1，
当AB＝BP时，同理可得x＝4（舍去）或﹣4，
当AP＝BP时，同理可得x＝78，
故点P的坐标为（9，0）或（﹣1，0）或（﹣4，0）或（78，0）．
三、解答题（8++8+8+8+8+10+10+12,共72分）
17. 已知二次函数y＝﹣x2+bx+c的图象如图所示，解决下列问题：
（1）关于x的一元二次方程﹣x2+bx+c＝0的解为　　；
（2）求此抛物线的解析式；
（3）当x为值时，y＜0；
（4）若直线y＝k与抛物线没有交点，直接写出k的范围．

【答案】-1或3
【分析】（1）直接观察图象，抛物线与x轴交于﹣1，3两点，所以方程的解为x1＝﹣1，x2＝3．
（2）设出抛物线的顶点坐标形式，代入坐标（3，0），即可求得抛物线的解析式．
（3）若y＜0，则函数的图象在x轴的下方，找到对应的自变量取值范围即可．
（4）若直线y＝k与抛物线没有交点，则k＞函数的最大值即可．
【解答】解：（1）观察图象可看对称轴出抛物线与x轴交于x＝﹣1和x＝3两点，
∴方程的解为x1＝﹣1，x2＝3，
故答案为：﹣1或3；
（2）设抛物线解析式为y＝﹣（x﹣1）2+k，
∵抛物线与x轴交于点（3，0），
∴（3﹣1）2+k＝0，
解得：k＝4，
∴抛物线解析式为y＝﹣（x﹣1）2+4，
即：抛物线解析式为y＝﹣x2+2x+3；
（3）若y＜0，则函数的图象在x轴的下方，由函数的图象可知：x＞3或x＜﹣1；
（4）若直线y＝k与抛物线没有交点，则k＞4函数的最大值，即y＞4．

18. 已知抛物线y＝x2﹣（2m+2）x+m2+2m其中m是常数．
（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点；
（2）若该抛物线的对称轴为直线x＝4．
①求该抛物线的函数解析式；
②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点．
【分析】 （1）要证明不论m为何值，该抛物线与x轴一定有两个公共点，只要证明b2﹣4ac＞0即可，然后代入数据计算即可；
（2）①根据该抛物线的对称轴为直线x＝4，可以求得m的值，从而可以得到抛物线的函数解析式；
②将①的函数解析式，化为顶点式，即可得到把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点．
【解答】 （1）证明：∵抛物线y＝x2﹣（2m+2）x+m2+2m其中m是常数，
∴[﹣（2m+2）]2﹣4×1×（m2+2m）
＝4m2+8m+4﹣4m2﹣8m
＝4＞0，
∴不论m为何值，该抛物线与x轴一定有两个公共点；
（2）①∵抛物线y＝x2﹣（2m+2）x+m2+2m的对称轴为直线x＝4，
∴−−2m+22×1=4，
解得m＝3，
∴该抛物线的解析式为y＝x2﹣8x+15；
②∵y＝x2﹣8x+15＝（x﹣4）2﹣1，
∴该抛物线沿y轴向上平移1个单位长度后，得到的抛物线与x轴只有一个公共点．
19. 在平面直角坐标系xOy中，二次函数y＝ax2+2x﹣3a（a≠0）交x轴于A、B两点（点A在点B的左侧），且抛物线的对称轴为直线x＝﹣1．
（1）求此抛物线的解析式及A、B两点坐标；
（2）若抛物线交y轴于点C，顶点为D，求四边形ABCD的面积．
【解答】解：（1）根据题意知，x＝−22a＝﹣1，则a＝1．
故该抛物线解析式是：y＝x2+2x﹣3．
因为y＝x2+2x﹣3＝（x+3）（x﹣1），
所以A（﹣3，0），B（1，0）；

（2）由（1）知，A（﹣3，0），B（1，0），
由抛物线y＝x2+2x﹣3知，C（0，﹣3）．
∵y＝x2+2x﹣3＝（x+1）2﹣4，
∴D（﹣1，﹣4）．
∴OA＝2，OC＝3，OE＝1，EB＝2，ED＝4，
∴S四边形ABCD＝S△BOC+S梯形OEDC+S△DAE＝12×1×3+12（3+4）×1+12×2×4＝9．即四边形ABCD的面积是9．

20. 有一家网红私人定制蛋糕店，她家的蛋糕经常供不应求，但每日最多只能做40只蛋糕，且每日做好的蛋糕全部订售一空．已知做x只蛋糕的成本为R元，售价为每只P元，且R、P与x的关系式为R＝500+30x，P＝170﹣2x，设她家每日获得的利润为y元．
（1）销售x只蛋糕的总售价为　　元（用含x的代数式表示），并求y与x的函数关系式；
（2）当每日做多少只蛋糕时，每日获得的利润为1500元？
（3）当每日做多少只蛋糕时，每日所获得的利润最大？最大日利润是多少元？
【答案】（-2x2+170x）
【解答】解：（1）销售x只蛋糕的总售价为（170﹣2x）x＝﹣2x2+170x（元），
根据题意，得：y＝（﹣2x2+170x）﹣（500+30x）＝﹣2x2+140x﹣500，
故答案为：（﹣2x2+170x）；

（2）当y＝1500时，得：﹣2x2+140x﹣500＝1500，
解得：x1＝20、x2＝50，
∵x≤40，
∴x＝20，
即当每日做20只蛋糕时，每日获得的利润为1500元；

（3）y＝﹣2x2+140x﹣500＝﹣2（x﹣35）2+1950，
∵a＝﹣2＜0，
∴当x＝35时，y取得最大值，最大值为1950，
答：当每日做35只蛋糕时，每日所获得的利润最大，最大日利润是1950元．
21. 已知，如图，抛物线y＝﹣x2+bx+c经过直线y＝﹣x+3与坐标轴的两个交点A，B．此抛物线与x轴的另一个交点为C．抛物线的顶点为D．
（1）求此抛物线的解析式．
（2）若点M为抛物线上一动点，是否存在点M．使△ACM与△ABC的面积相等？若存在，求点M的坐标；若不存在，请说明理由．

【解答】解：（1）∵直线y＝﹣x+3，
∴当x＝0时，y＝3，当y＝0时，x＝3，
∵直线y＝﹣x+3与坐标轴的两个交点A，B，
∴点A的坐标为（3，0），点B的坐标为（0，3），
∵抛物线y＝﹣x2+bx+c经过直线y＝﹣x+3与坐标轴的两个交点A，B，
-32+3b+c=0 c=3
∴b=2 c=3
即抛物线的解析式为y＝﹣x2+2x+3；
（2）存在点M．使△ACM与△ABC的面积相等．
∵抛物线y＝﹣x2+2x+3＝﹣（x﹣3）（x+1）＝﹣（x﹣1）2+4与x轴的另一个交点为C．抛物线的顶点为D，
∴点C的坐标为（﹣1，0），点D的坐标为（1，4），
∵△ACM与△ABC的面积相等，点B的坐标为（0，3），
∴点M的纵坐标是3或﹣3，
当点M的纵坐标为3时，3＝﹣x2+2x+3，得x1＝0，x2＝2，
则点M的坐标为（2，3）；
当点M的纵坐标为﹣3时，﹣3＝﹣x2+2x+3，得x3＝√7+1，x4＝﹣√7+1，
则点M的坐标为（√7+1，﹣3）或（﹣√7+1，﹣3）；
由上可得，点M的坐标为（2，3）、（√7+1，﹣3）或（﹣√7+1，﹣3）．
【知识点】抛物线与x轴的交点、一次函数图象上点的坐标特征、二次函数的性质、待定系数法求二次函数解析式、二次函数图象上点的坐标特征
22. 某客商准备购一批特色商品，经调查，用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍，一件A型商品的进价比一件B型商品的进价多10元．
（1）求一件A，B型商品的进价分别为多少元？
（2）若该客商购进A，B型商品共250件进行试销，其中A型商品的件数不大于B型的件数，且不小于20件．已知A型商品的售价为240元/件，B型商品的售价为220元/件，且全部售出．设购进A型商品m件，
①写出m的取值范围　　；
②求出商场销售这批商品的最大利润，并求出此时的进货方案．
（3）若m的范围与（2）保持一致，但是A型商品的售价与A型商品销量之间的关系如下表所示：
A型商品的售价
240
230
220
210
200
……
A型商品的销量
0
5
10
15
20
……
B型商品的售价降为210元/件，且全部售出．设购进A型商品m件，求出这批商品的最大利润，并求出此时的进货方案．
【答案】20≤m≤125
【解答】解：（1）设一件B型商品的进价为x元，则一件A型商品的进价为（x+10）元．
由题意：16000/(x+10)=15000/x
解得x＝150，
经检验x＝150是分式方程的解，
x+10＝160，
答：一件B型商品的进价为150元，则一件A型商品的进价为160元；

（2）①因为客商购进A型商品m件，所以客商购进B型商品（250﹣m）件．
由题意：
m≥20
m≤250-m
解得，20≤m≤125，
故答案为：20≤m≤125；
②设商场销售这批商品的利润为w元，根据题意得，
w＝m（240﹣160）+（220﹣150）（250﹣m）＝10m+17500，
∵10＞0，
∴w随m的增大而增大，
∵20≤m≤125，
∴当m＝125时，w取最大值为10×125+17500＝18750（元），
此时进货方案是：A商品进125件，B商品进125件，
答：商场销售这批商品的最大利润为18750元，此时的进货方案：A商品进125件，B商品进125件；
（3） 由表中数据可知，商品A的售价与销量是一次函数关系，可设为y＝km+b（k≠0），代入两组数据得，
b=240
5k+b=230
k=-2
b=240
∴y＝﹣2m+240，
设总利润为w元，根据题意得，
w＝m（﹣2m+240﹣160）+（210﹣150）（250﹣m）＝﹣2m2+20m+15000＝﹣2（m﹣5）2+15050，
∵﹣2＜0，
∴当m＞5时，w随m的增大而减小，
∵20≤m≤125，
∴当m＝20时，w有最大值为w＝﹣2×（20﹣5）2+15050＝14600，
此时进货方案为：A商品进20件，B商品进货230件，
答：这批商品的最大利润为14600元，此时的进货方案是A商品进20件，B商品进货230件．
23. 如图，已知二次函数图象的顶点坐标为C（1，0），直线y＝x+m的图象与该二次函数的图象交于A、B两点，其中A点坐标为（3，4），B点在y轴上．
（1）求m的值及这个二次函数的解析式；
（2）若P是线段AB下方抛物线上一动点，当△ABP面积最大时，求P点坐标以及△ABP面积最大值；（3）若D为直线AB与这个二次函数图象对称轴的交点，Q为线段AB之间的一个动点，过Q作x轴的垂线，与这个二次函数图象交于点E，问是否存在这样的点Q，使得四边形DCEQ为平行四边形，若存在，请求出Q点的坐标；若不存在，请说明理由．

【解答】解：（1）∵点A（3，4）在直线y＝x+m上，
∴4＝3+m．
∴m＝1．
设所求二次函数的关系式为y＝a（x﹣1）2．
∵点A（3，4）在二次函数y＝a（x﹣1）2的图象上，
∴4＝a（3﹣1）2，
∴a＝1．
∴所求二次函数的关系式为y＝（x﹣1）2．
即y＝x2﹣2x+1；
（2）过点P作y轴的平行线交AB于点E，

则△ABP面积＝S△PEA+S△PEB＝12PE•（xA﹣xB）＝12×[（x+1）﹣（x2﹣2x+1）]×3＝﹣32x2+92x，
∵﹣32＜0，故△ABP面积存在最大值，当x＝32时，△ABP面积最大值为98，
此时点P的坐标为（32，14）；
（3）存在．
理由：要使四边形DCEQ是平行四边形，必需有QE＝DC．

∵点D在直线y＝x+1上，
∴点D的坐标为（1，2），
∴﹣x2+3x＝2．
即x2﹣3x+2＝0．
解之，得x1＝2，x2＝1（不合题意，舍去）
∴当Q点的坐标为（2，3）时，四边形DCEQ是平行四边形．
24. 如图，已知二次函数的图象经过点A（4，4），B（5，0）和原点O，P为二次函数图象上的一个动点，过点P作x轴的垂线，垂足为D（m，0），并与直线OA相较于点C．
（1）求出二次函数的解析式；
（2）当点P在直线OA的上方时，求线段PC的最大值；
（3）当点P在直线OA的上方时，是否存在一点P，使射线OP平分∠AOy，若存在，请求出P点坐标；若不存在．请说明理由；
（4）当m＞0时，探索是否存在点P，使得△PCO为等腰三角形，若存在，求出P点的坐标；若不存在，请说明理由．

【解答】解：（1）∵二次函数的图象经过原点，
∴设二次函数的解析式为y＝ax2+bx，
将A（4，4），B（5，0）代入，
得16a+4b=4
25a+5b=0，
解得，a＝﹣1，b＝5，
∴y＝﹣x2+5x；

（2）设直线OA的解析式为y＝ax，
将A（4，4）代入，
得，a＝1，
∴yOA＝x，
∵PD⊥x轴，D（m，0），
∴P（m，﹣m2+5m），C（m，m），
∴PC＝﹣m2+5m﹣m
＝﹣m2+4m
＝﹣（m﹣2）2+4，
根据二次函数的图象及性质可知，当m＝2时，PC有最大值，其最大值为4；

（3）存在，理由如下：
如图，当射线OP平分∠AOy时，过点P作PM⊥y轴于点M，作PN⊥OA于点N，
则PM＝PN，
∵点C在直线yOA＝x上，
∴△ODC是等腰直角三角形，
∴∠OCD＝∠PCN＝45°，
∴△PCN是等腰直角三角形，
由（2）知，PC＝﹣m2+4m，
∴PN＝√2/2（﹣m2+4m）＝﹣√2/2m2+2√2m，
∵P（m，﹣m2+5m），
∴PM＝m，
∵PM＝PN，
∴m＝﹣√2/2m2+2√2m，
解得，m1＝0（舍去），m2＝4﹣√2，
∴P（4﹣√2，2+3√2）；

（4）存在，理由如下：
∵∠PCO＝180°﹣∠OCD＝135°，
∴当△PCO为等腰三角形时，只存在PC＝OC一种情况，
由（2）知，PC＝﹣m2+4m，OC＝√2OD＝√2m，
∴﹣m2+4m＝√2m，
解得，m1＝0（舍去），m2＝4﹣√2，
∴当m＝4﹣√2时，﹣m2+5m＝2+3√2，
∴P（4﹣√2，2+3√2）．