初中数学冀教版七年级上册1.3 绝对值与相反数教课内容课件ppt

这是一份初中数学冀教版七年级上册1.3 绝对值与相反数教课内容课件ppt，共40页。PPT课件主要包含了的相反数是0等内容，欢迎下载使用。

有理数王国的公民+1一天不小心掉进了一个魔瓶里。谁知出来后竟变成胖乎乎的0，你说怪不怪？冷眼旁观的2说：“谁叫这瓶里睡着他的相反数兄弟呢？幸好我兄弟不在里面！”同学们，你想知道+1的相反数兄弟是谁？为什么他俩见面后就变成0呢？就让我们一起走进神奇的相反数的世界吧!
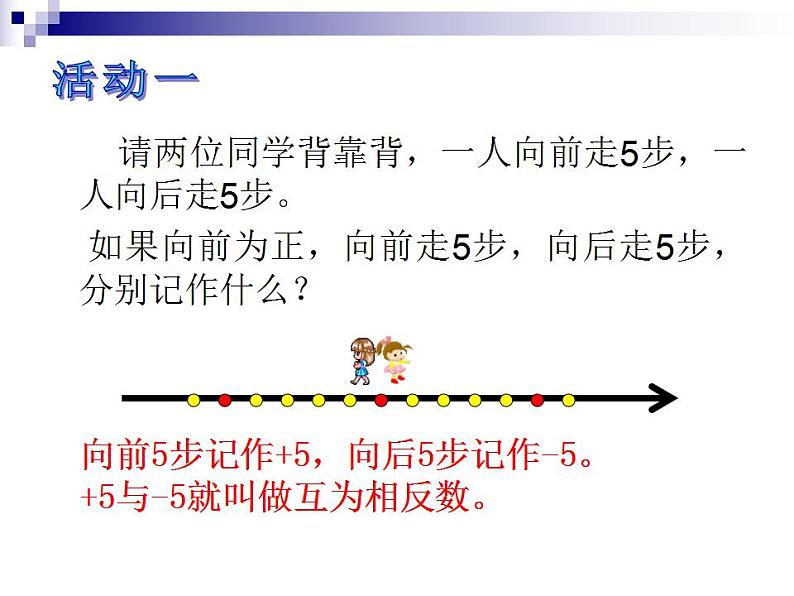
请两位同学背靠背，一人向前走5步，一人向后走5步。 如果向前为正，向前走5步，向后走5步，分别记作什么？
向前5步记作+5，向后5步记作-5。+5与-5就叫做互为相反数。
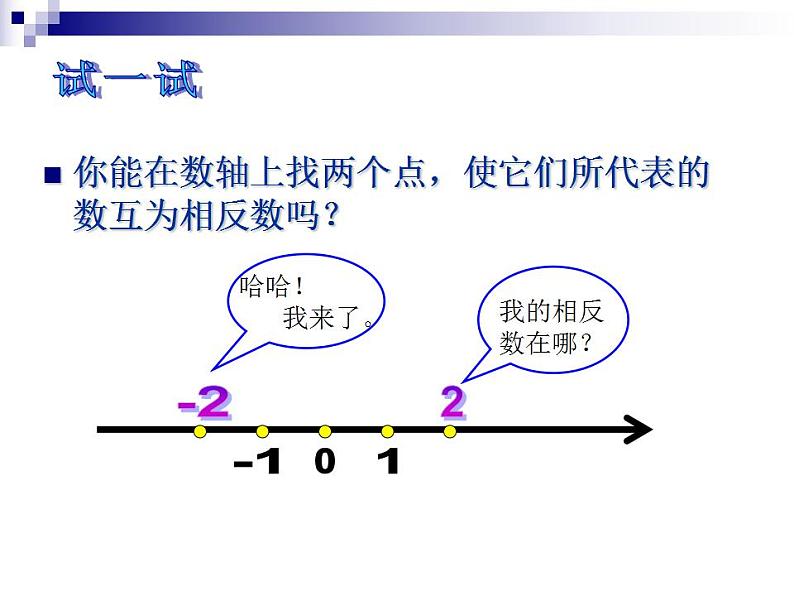
你能在数轴上找两个点，使它们所代表的数互为相反数吗？
具备什么样特点的两个数才互为相反数呢？（小组讨论）
像+2与-2，+5与-5这样只有符号不同两个数叫做互为相反数
（－９，７，０， 0.2）
（ 2.4，1.7，－１）
a 的相反数是-a ， a可表示任意数——正数、负数、0，求任意一个数的相反数就可以在这个数前加一个“－”号．
提出问题：若把 a分别换成＋5，－7，0时，这些数的相反数怎样表示？
a = +5， -a = -（+5） a = -7， - a = -（-7）a = 0， -a = 0
－（＋1.1）表示什么？－（－7）呢，－（－9.8）呢？它们的结果应是多少？
例题1 －４是____的相反数， ．．(2) 是_____的相反数， ．
※多重符号的化简方法：
“数数负号，偶正奇负.”
在一个数前面加上“－”号表示求这个数的相反数，如果在这些数前面加上“＋”号呢？
在一个数前面加上“＋”仍表示这个数，“＋”号可省略．
　　在数轴上表示相反数(0除外)的两个点位于原点的　　　,且与原点的距离　　.
数轴上表示相反数的两个点和原点有什么关系？
6．数轴上到原点距离相等的点表示的数的关系（ ）
A、互为倒数 B、互为相反数 C、相等 D、没有关系
7．下列说法正确的是（ ）
A、-2是相反数 B、数轴上表示相反数的点一定在原点两侧 C、a与-a互为相反数，其中a为正数，-a为 负数D、只有符号不同的两数不一定是相反数。
8．若x= -5， 则 -[ -( -x )]= ．
A、5 B、-5
请一位同学随便报一个数，然后点名叫另一位同学说出它的相反数。
总结：a的相反数是-a。0的相反数是0
1、两只小狗从同一点Ｏ出发，在一条笔直的街上跑，一只向右跑3米到达Ａ点，另一只向左跑3米到达Ｂ点。若规定向右为正，则Ａ处记做_______，Ｂ处记做_______。２、这两只小狗在跑的过程中，有没有共同的地方？在数轴上的Ａ、Ｂ两又有什么特征？
小 结：在实际生活中，有时存在这样的情况，无需考虑数的正负性质，比如：在计算小狗所跑的路程中，与小狗跑的方向无关，这时所走的路程只需用正数，这样就引进了一个新的概念———绝对值。
绝对值：一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
∵ －5到原点的距离是5，∴ －5的绝对值是5，记|－5|=5；又：5的绝对值是5，记做|5|=5。
注意：①与原点的关系 ②是一个距离的概念
例1：求下列各数的绝对值：
思考：通过刚才的练习，你有什么发现？
例2、求绝对值等于4的数 。
注意:说明符号“∵”读作“因为”，“∴”读作“所以”
∵数轴上到原点的距离等于4个单位长度的点 有两个,即表示＋4的点P和表示－4的点M
∵|＋4|=4， |－4|=4
∴绝对值等于4的数是＋4和－4
∴绝对值等于4的数是＋4和－4
互为相反数的两个数的绝对值相等.
1、一个正数的绝对值是它本身
2、一个负数的绝对值是它的相反数
4、互为相反数的两个数的绝对值相等
正数的绝对值是它本身；（涛声依旧）负数的绝对值是它的相反数；（物是人非）0的绝对值是0。
请同学们把自己最喜欢的数写给同桌，由他（她）写出这个数的绝对值。
小窍门：在写一个数的绝对值时，首先判断这个数是正数，负数，还是零，然后再选择相应法则。
( 1 )在数轴上表示下列各数，并比较它们的大小： - 1.5 ， - 3 ， - 1 ， - 5 ( 2 ) 求出（1）中各数的绝对值，并比较它们的大小 （ 3 ）你发现了什么？
- 5 ＜ - 3 ＜- 1.5 ＜ - 1
（2）| -1.5 | = 1.5 ； | - 3 | =3； | -1 | = 1 ； | - 5 | = 5．
（3）由以上知：两个负数比较大小，绝对值大的反而小
1 ＜ 1.5 ＜3 ＜5
解法一（利用绝对值比较两个负数的大小）
解: (1)| -1| = 1，| -5 | = 5 ，1﹤5， 所以 - 1＞ - 5
解法二 （利用数轴比较两个负数的大小）
因为- 5在 –1左边,所以 - 5﹤ - 1
| 5 - 1 | = （ ）
1 + | -5 | =（ ）
| 5 | - | -3 | =（ ）
| -1 | × | -2 | =（ ）
| -6.2 | ÷ | +2 | =（ ）
分析：先求算式中绝对值的值，然后进行四则运算。
（1）一个数的绝对值一定是正数。 （ ）
（2）一个数的绝对值不可能是负数。 （ ）
（3）互为相反数的两个数，它们的绝对值 一定相等。 （ ）
（4）绝对值是同一个正数的数有两个，且 它们是互为相反数。 （ ）
(1)如果a＞0，那么|a|＝a (2)如果a＜0，那么|a|＝－a (3)如果a＝0，那么|a|＝0　　　　
问题1：字母a表示一个数，-a表示什么？-a一定是负数吗？问题2：如果数a的绝对值等于a，那么a可能是正数吗？可能是负数吗？可能是零吗？问题3：如果数a的绝对值等于-a，那么a可能是正数吗？可能是负数吗？可能是零吗？
练习：回答下列问题①一个数的绝对值是它本身，这个数是什么数？②一个数的绝对值是它的相反数，这个数是什么数？③一个数的绝对值一定是正数吗？④一个数的绝对值不可能是负数，对吗？
正数公司和负数公司招聘职员，要求是：经过绝对值符号“︱︱”这扇大门后，结果为正就是正数公司职员，结果为负就是负数公司职员。
负数公司能招到职员吗？0能找到工作吗？
总结：任何一个数的绝对值一定是非负数。
绝对值 ：在数轴上，一个数所对应的点与原点的距离叫做该数的绝对值.
正数的绝对值是它本身; 负数的绝对值是它的相反数; 0 的绝对值是 0.
（2.代数定义）
会利用绝对值比较两个负数的大小： 两个负数，绝对值大的反而小.
1.说说你对相反数的认识。
相反数成对出现。只有符号不同的两个数才互为相反数。数轴上表示相反数的两个对应点，分别位于原点两侧，它们到原点距离相等。
2.对于绝对值你有什么认识？
求一个数的绝对值要先判断它的符号。互为相反数的两个数的绝对值相等。绝对值一定是非负数。