数学拓展模块3.5 正态分布教案及反思

第13讲  正态分布

教学目的：理解并熟练掌握正态分布的密度函数、分布函数、数字特征及线性性质。

教学重点：正态分布的密度函数和分布函数。

教学难点：正态分布密度曲线的特征及正态分布的线性性质。

教学学时：2学时

教学过程:

第四章  正态分布

§4.1 正态分布的概率密度与分布函数

在讨论正态分布之前，我们先计算积分。

首先计算。因为

(利用极坐标计算)

所以。

记，则利用定积分的换元法有

因为，所以它可以作为某个连续随机变量的概率密度函数。

定义  如果连续随机变量的概率密度为

则称随机变量服从正态分布,记作,其中是正态分布的参数。正态分布也称为高斯（Gauss）分布。

对于的特殊情况,即如果,则称服从标准正态分布,它的概率密度记为,有。

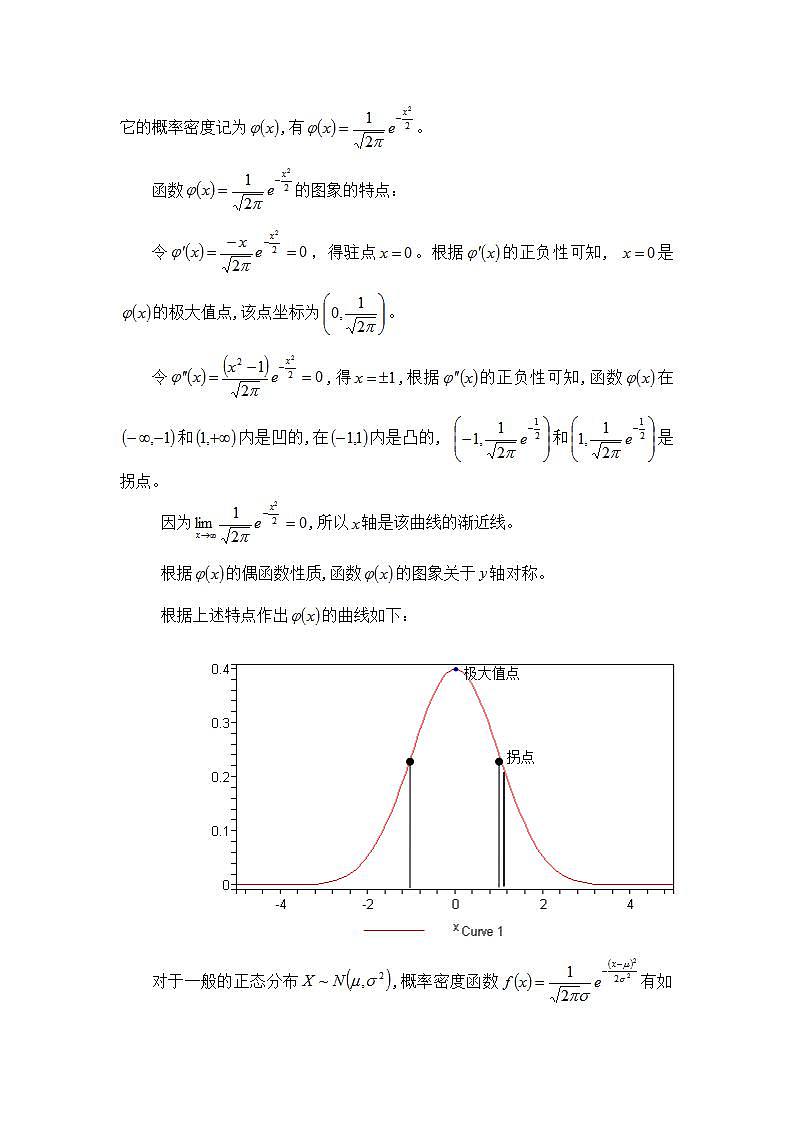
函数的图象的特点：

令，得驻点。根据的正负性可知, 是的极大值点,该点坐标为。

令,得,根据的正负性可知,函数在和内是凹的,在内是凸的, 和是拐点。

因为,所以轴是该曲线的渐近线。

根据的偶函数性质,函数的图象关于轴对称。

根据上述特点作出的曲线如下：

对于一般的正态分布,概率密度函数有如下特点：

(1)在处达到极大值，极大值点为。

(2)在处为图象的拐点，拐点坐标为,在内是凸的,其它范围内是凹的。

(3)轴为渐近线。

(4)越大，最大值越小，拐点越偏离。

(5)图象关于直线对称。

对于,它的分布函数为

对于,记它的分布函数为。

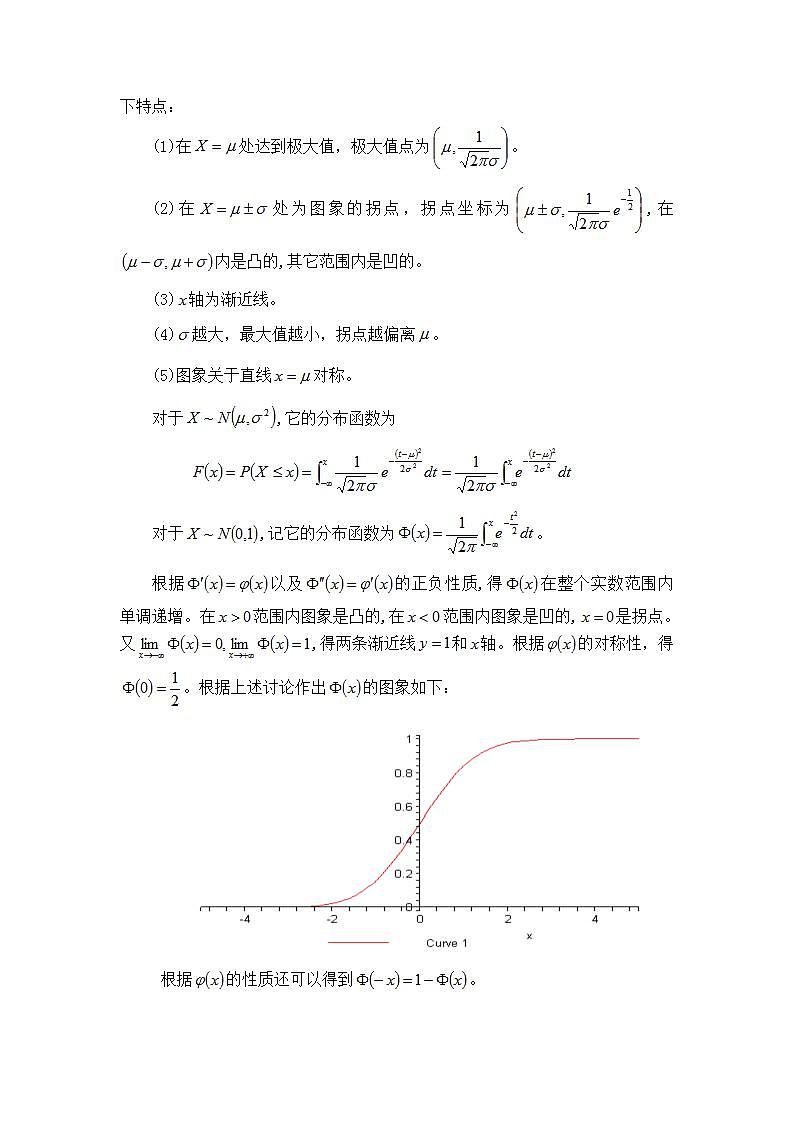
根据以及的正负性质,得在整个实数范围内单调递增。在范围内图象是凸的,在范围内图象是凹的,是拐点。又,得两条渐近线和轴。根据的对称性，得。根据上述讨论作出的图象如下：

根据的性质还可以得到。

的直接计算是比较困难的,但可以通过查表得到在时的数值。对于的情况，可以根据求得。

一般的正态分布的分布函数与的关系如下：

有了与的关系，就可以求出任何正态随机变量落在某个区间内的概率。

对于,某两个数满足,则有

又因为是连续随机变量,因此有

例1  已知,求和。

解 服从参数的正态分布,故有

例2 已知,求,。

解

例3 已知,求随机变量的概率密度函数。

解 因为,所以的密度函数,则的分布函数。

显然当时,,此时。

对于的情况有

此时

故随机变量的概率密度函数为

注 称上述随机变量服从自由度为1的分布。

§4.2 正态分布的数字特征

我们首先讨论一般正态分布与标准正态分布数字特征间的关系。

由一般正态分布的分布函数与标准正态分布的分布函数的关系可知，如果随机变量,则。由期望与方差的线性性质知，因此,要研究正态分布的数字特征,只需研究标准正态分布的数字特征就可以了。

1. 正态分布的数学期望

对于,

对于,

2. 正态分布的方差

对于,,已知，

所以。

对于,。

综合上面的讨论知，正态分布的期望值是,方差是。

§4.3 正态分布的线性性质

1. 单个正态随机变量线性函数的分布

已知,,记随机变量,下面讨论的性质。

因为, ,故有

由此可见，既单个正态随机变量的线性函数仍然服从正态分布。

2. 两个正态随机变量和的分布

已知两个独立的随机变量满足,,则仍然服从正态分布。由数字特征的线性性质可得

因此有。

对于上述结论不予证明,其有更广泛的结论。

定理  设随机变量相互独立，都服从正态分布

则它们的线性组合也服从正态分布，且有

其中为常数。