苏科版八年级上册2.5 等腰三角形的轴对称性图片ppt课件

这是一份苏科版八年级上册2.5 等腰三角形的轴对称性图片ppt课件，共34页。PPT课件主要包含了情境引入，探究活动，问题二，归纳总结，定理证明，则有∠1＝∠2，AB＝AC，∠1＝∠2，AD＝AD，∴∠B＝∠C等内容，欢迎下载使用。
1. 观察图中的等腰三角形ABC，分别说出它们的腰、底边、顶角和底角.
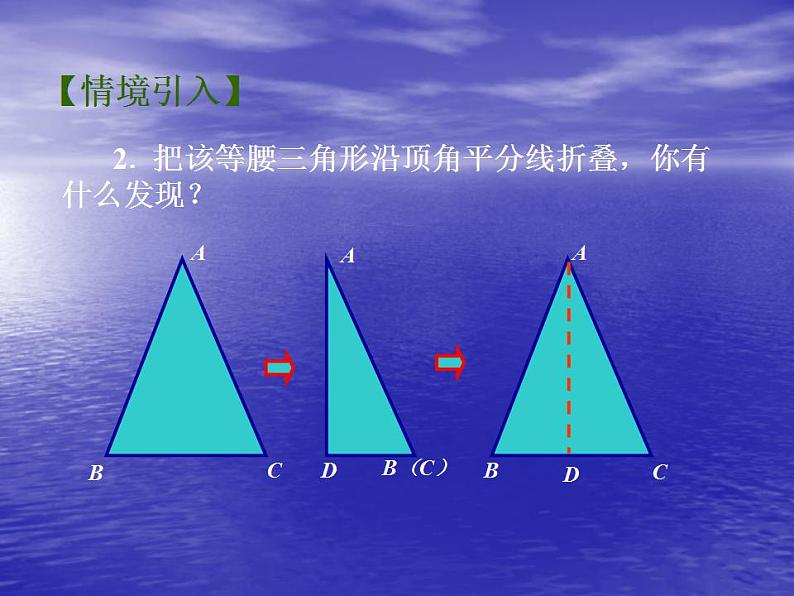
2. 把该等腰三角形沿顶角平分线折叠，你有什么发现？
问题一：等腰三角形是轴对称图形吗？它的对称轴是什么？
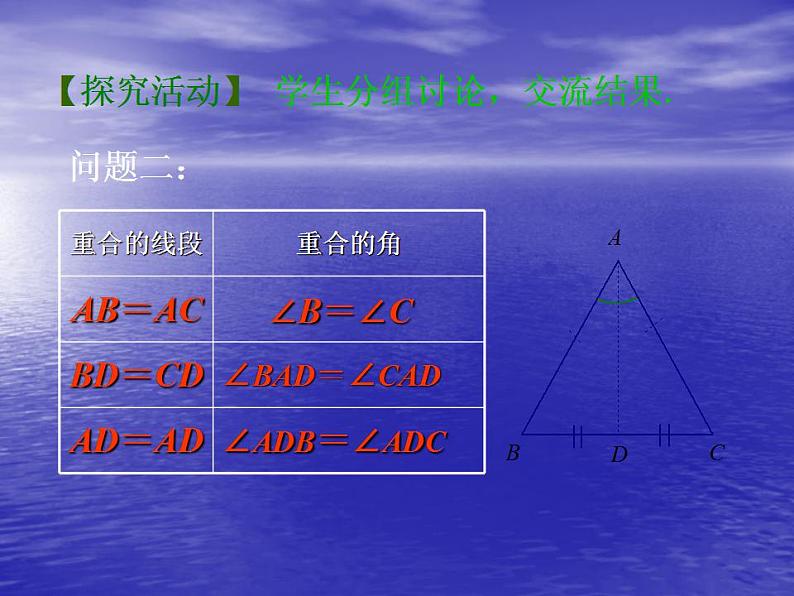
问题二：找出等腰三角形ABC对折后重合的线段和角.
问题三：由这些重合的线段和角，你能发现等腰三角形的哪些性质呢？说一说你的猜想.
学生分组讨论，交流结果．
问题一：等腰三角形是轴对称图形.　　等腰三角形的顶角平分线（底边上的高、中线）所在直线是它的对称轴.
学生分组讨论，交流结果.
问题三：等腰三角形是轴对称图形.
　　等腰三角形的顶角平分线（底边上的高、中线）所在直线是它的对称轴.
　　等腰三角形的两个底角相等.
　　等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
我们有如下定理：　　等腰三角形的两底角相等.　　等腰三角形底边上的高线、中线及顶角平分线重合.
思考：如何证明这个定理？
在△ABD和△ACD中，
证明：作顶角的平分线AD，
∴ △ABD≌ △ACD
（全等三角形对应角相等）
思考：你还可用什么方法证明上述定理？
按下列作法，用直尺和圆规作等腰三角形ABC，使底边BC＝a,高AD＝h.
本节课你的收获是什么？
等腰三角形的轴对称性（2）
2．顶角的角平分线、底边上的中线、底边上的高三线合一．
问题：如右图所示△ABC是等腰三角形，AB＝AC，倘若一不留心，它的一部分被墨水涂没了，只留下一条底边BC和一个底角∠C．同学们想一想，有没有办法把原来的等腰三角形ABC重新画出来？大家试试看．
方法一：用角的相等来画.
方法二：用过一边中点作垂线的方法来画.
请同学们分别拿出一张半透明纸，做一个实验，按以下方法进行操作：
1．在半透明纸上画一条长为6cm的线段BC．
2．以BC为始边，分别以点B和点C为顶点，用量角器画两个相等的锐角，两角终边的交点为A．
3．用刻度尺找出BC的中点D，连接AD，然后沿AD对折．
问题：AB与AC是否重合？重合
在△BAT和△CAT中，　 ∠1＝∠2(角平分线定义)， ∠B＝∠C(已知)， AT＝AT(公共边) ， ∴△BAT≌△CAT(AAS)，∴AB＝AC(全等三角形对应边相等)．
已知：在△ABC中，∠B＝∠C 求证：AB＝AC．
证明：（1）作∠A的平分线交BC于T．
（2）过A点作AD⊥BC，垂足为D．
∵AD⊥BC，∴∠ADB＝∠ADC，在△ADB和△ADC中，　 ∠ADB＝∠ADC， ∠B＝∠C， AD＝AD，∴△ADB≌△ADC，∴AB＝AC．
思考：通过这题的证明你发现了什么结论？
如果一个三角形有两个角相等,那么这两个角所对的边也相等
( 简称“等角对等边”)．
∵∠B＝∠C∴AB＝AC (等角对等边)
请思考： 　　 “等边对等角”与“等角对等边” 是否一样？它们的主要区别在哪里？
（它们的条件与结论正好调换了位置）．
通过本节课的学习：（1）你有哪些收获？（2）你还有什么疑惑？
等腰三角形的轴对称性（3）
问题：等腰三角形有哪些性质？等边对等角，三线合一，轴对称形等等
1.已知：如图，∠EAC是△ABC的外角，AD平分 ∠EAC，AD∥BC． 求证：AB＝AC．
证明：∵ AD平分 ∠EAC∴∠EAD=∠CAD∵ AD∥BC∴∠EAD=∠B，∠C=∠CAD又∴∠EAD=∠CAD∴ ∠B=∠C∴ AB＝AC
如图，如果AB＝AC，AD∥BC，那么AD平分∠EAC吗？试证明你的结论．
证明：∵ AB＝AC∴ ∠B=∠C∵ AD∥BC∴∠EAD=∠B，∠C=∠CAD∴∠EAD=∠CAD即AD平分 ∠EAC
如图，如果AB＝AC，AD平分∠EAC，那么AD∥BC吗？
证明：∵ AD平分 ∠EAC∴∠EAC=2∠CAD∵ AB＝AC∴ ∠B=∠C又∵∠EAC=∠C+∠B∴∠EAC=2∠C∴∠C=∠CAD∴AD∥BC
你能用折纸的方法将一个直角三角形分成两个等腰三角形吗？
1．任意剪出一张直角三角形纸片（如图1）．
2．剪得的纸片是否能折成图2的形状？
3．△ACD与△BCD为什么是等腰三角形？请说明理由．
　　直角三角形斜边上的中线等于斜边的一半．
（1）Rt△ABC中，如果斜边AB 为4cm，那么斜边上的中线CD＝______cm．
（2）如图，在Rt△ABC中，CD是斜边AB上的中线，DE⊥AC ，垂足为E． ①如果CD＝2.4cm，那么AB＝ cm． ②写出图中相等的线段和角．
∠ACB=∠DEA=∠DEC=90°．
（3）在Rt△ABC中，∠ACB＝90°，CA＝CB，如果斜边AB＝5cm，那么斜边上的高CD＝ cm．
1．如图，Rt△ABC，∠ACB＝90°，如果∠A＝30°，那么BC与AB有怎样的数量关系？试证明你的结论．
证明：作斜边上的中线CD，∵∠ACB＝90°，∠A＝30°，∴∠B＝60°．∵∠ACB＝90°，CD是斜边上的中线，∴
∴△BCD是等边三角形（有一个角是60°的等腰三角形是等边三角形）．∴ ．
（直角三角形斜边上的中线等于斜边的一半）．