高中数学人教版新课标A必修2第一章 空间几何体1.2 空间几何体的三视图和直观图教案设计

1.1.2　圆柱、圆锥、圆台、球的结构特征

Q

观察下列实物图，你能说明由该实物图抽象出的几何体与多面体有何不同吗？

X

1．圆柱的结构特征

[归纳总结]　圆柱的简单性质：

(1)圆柱有无数条母线，它们平行且相等．

(2)平行于底面的截面是与底面大小相同的圆，如图①所示．

(3)过轴的截面(轴截面)都是全等的矩形，如图②所示．

(4)过任意两条母线的截面是矩形，如图③所示．

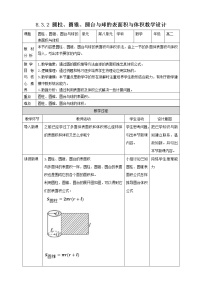
2．圆锥的结构特征

[归纳总结]　圆锥的简单性质：

(1)圆锥有无数条母线，它们有公共点即圆锥的顶点，且长度相等．

(2)平行于底面的截面都是圆，如图①所示．

(3)过轴的截面(轴截面)是全等的等腰三角形，如图②所示．

(4)过任意两条母线的截面是等腰三角形，如图③所示．

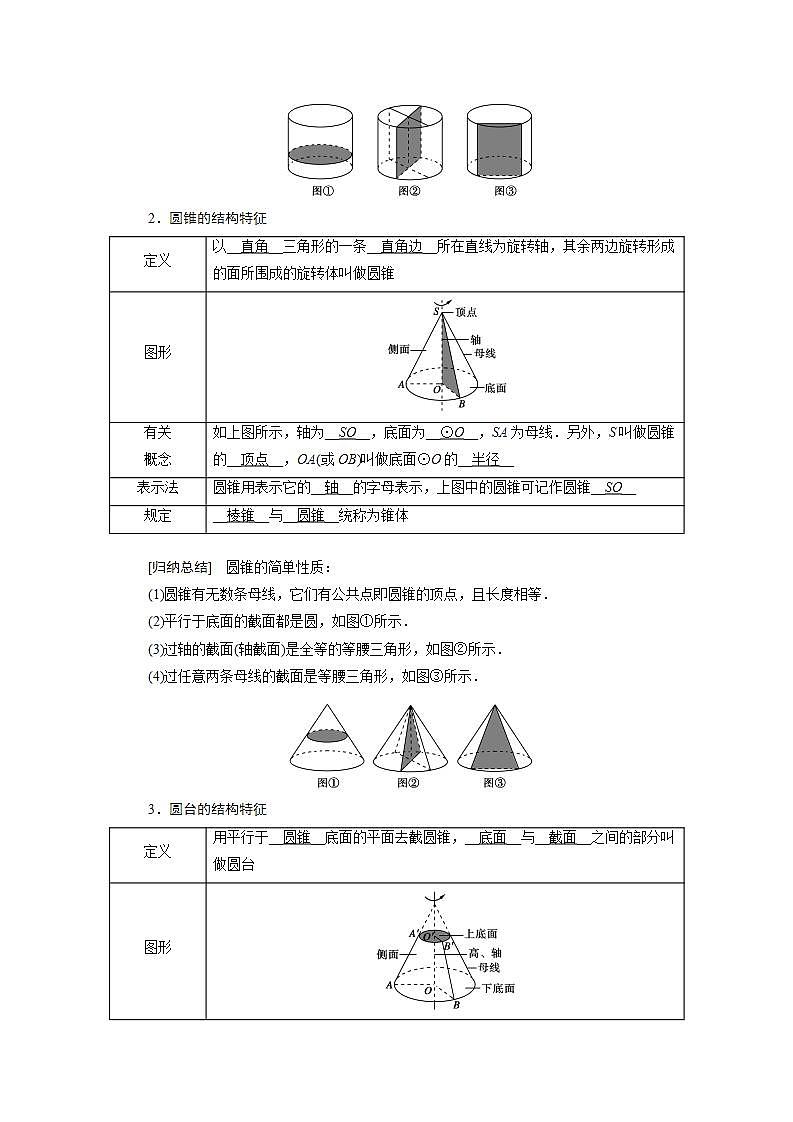
3．圆台的结构特征

[归纳总结]　圆台的简单性质：

(1)圆台有无数条母线，且它们相等，延长后相交于一点．

(2)平行于底面的截面是圆，如图①所示．

(3)过轴的截面是全等的等腰梯形，如图②所示．

(4)过任意两条母线的截面是等腰梯形，如图③所示．

4．球

Y

1．下列几何体中是旋转体的是 (　D　)

①圆柱；②六棱锥；③正方体；④球体；⑤四面体．

A．①和⑤ B．①　　

C．③和④ D．①和④

[解析]　①④是旋转体，②③⑤是多面体，故选D．

2．球的任意两条直径不一定具有的性质是 (　C　)

A．相交  B．平分

C．垂直  D．都经过球心

[解析]　球的任意两条直径不一定垂直．

3．如图所示的组合体，其结构特征是 (　D　)

A．两个圆锥 B．两个圆柱

C．一个棱锥和一个棱柱 D．一个圆锥和一个圆柱

[解析]　如图所示的几何体是由一个圆锥和一个圆柱构成的组合体．

4．关于圆台，下列说法正确的是__②③④__.

①两个底面平行且全等；

②圆台的母线有无数条；

③圆台的母线长大于高；

④两底面圆心的连线是高．

[解析]　圆台的上底面和下底面是两个大小不同的圆，则①不正确，②③④正确．

H

命题方向1　⇨旋转体的结构特征　　

典例1 下列命题正确的是__④⑥⑧__.

①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥；

②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台；

③圆柱、圆锥、圆台的底面都是圆；

④以等腰三角形的底边上的高所在的直线为旋转轴，其余各边旋转一周形成的曲面围成的几何体是圆锥；

⑤球面上四个不同的点一定不在同一平面内；

⑥球的半径是球面上任意一点和球心的连线段；

⑦球面上任意三点可能在一条直线上；

⑧用一个平面去截球，得到的截面是一个圆面．

[思路分析]　准确理解旋转体的定义，在此基础上掌握各旋转体的性质，才能更好地把握它们的结构特征，以作出准确的判断．

[解析]　①以直角三角形的一条直角边为轴旋转一周才可以得到圆锥；②以直角梯形垂直于底边的一腰为轴旋转一周可得到圆台；③它们的底面为圆面；④正确；作球的一个截面，在截面的圆周上任意取四点，则这四点就在球面上，故⑤错误；根据球的半径定义可知⑥正确；球面上任意三点一定不共线，故⑦错误；用一个平面去截球，一定截得一个圆面，故⑧正确．　　

『规律方法』　圆柱、圆锥、圆台、球都是常见的旋转体，熟练掌握它们结构特征，弄清旋转体的性质是准确作图解题的前提．

〔跟踪练习1〕 

下列命题：①任意平面截圆柱，截面都是圆面；②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下两底面的圆周上各取一点，则这两点的连线是圆台的母线，其中正确的是(　D　)

A．①②　　 B．②③　　

C．①③　　 D．②

[解析]　过两母线的截面为矩形，有时斜的截面为椭圆，故①错；根据母线的定义和特点，③错误，原因是圆柱的母线都是平行的．圆台的母线不是上底面和下底面上任意两点的连线，②正确，故选D．

命题方向2　⇨简单组合体的结构特征

典例2 如图，绕虚线旋转一周后形成的旋转体是由哪些简单几何体组成的？

[解析]　如图所示，由一个圆锥O4O5，一个圆柱O3O4及一个圆台O1O3中挖去圆锥O1O2组成的．

『规律方法』　平面图形绕某条直线旋转时，要过有关顶点向轴作垂线，然后分析旋转体的结构和组成．

〔跟踪练习2〕 

已知AB是直角梯形ABCD中与底边垂直的一腰，如右图．分别以AB，BC，CD，DA为轴旋转，试说明所得几何体的结构特征．

[解析]　(1)以AB为轴旋转所得旋转体是圆台．如下图①所示．

(2)以BC边为轴旋转所得的旋转体是一组合体：下部为圆柱，上部为圆锥．如下图②所示．

(3)以CD边为轴旋转所得的旋转体为一组合体：上部为圆锥，下部为圆台，再挖去一个小圆锥．如下图③所示．

(4)以AD边为轴旋转所得的组合体：一个圆柱上部挖去一个圆锥．如下图④所示．

命题方向3　⇨旋转体中的计算问题

典例3 如图所示，用一个平行于圆锥SO底面的平面截这个圆锥，截得圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3 cm，求圆台O′O的母线长.

[思路分析]　旋转体的轴截面中有母线、底面半径、高等主要元素，因而，在涉及这些元素的计算时，通常利用轴截面求解．在圆台的轴截面中，将等腰梯形的两腰延长，在三角形中可借助相似求解．这种立体问题平面化是解答旋转体中计算问题最常用的方法．

[解析]　设圆台的母线长为l cm，由截得圆台上、下底面面积之比为1∶16，可设截得圆台的上、下底面的半径分别为r，4r.过轴SO作截面，如图所示．

则△SO′A′∽△SOA，SA′＝3 cm．

∴＝.∴＝＝．

解得l＝9(cm)

即圆台的母线长为9 cm．

『规律方法』　用平行于底面的平面去截柱、锥、台等几何体，注意抓住截面的性质(与底面全等或相似)，同时结合旋转体中的经过旋转轴的截面(轴截面)的性质，利用相似三角形的性质，构设相关几何变量的方程组而得解．

〔跟踪练习3〕 

一个圆台的母线长为12 cm，两底面面积分别为4π cm2和25π cm2.求：

(1)圆台的高；

(2)截得此圆台的圆锥的母线长．

[解析]　如图，将圆台恢复成圆锥后作其轴截面，设圆台的高为h cm，截得该圆台的圆锥的母线为x cm，由条件可得圆台上底半径r′＝2 cm，下底半径r＝5 cm．

(1)由勾股定理得

h＝＝3(cm)．

(2)设圆锥的母线长为x，由三角形相似得：＝，解得x＝20(cm)．

Y 　旋转体的概念不清致误

典例4 如图所示，它们是不是棱锥、棱台、圆柱、圆锥等几何体？

[错解]　图①是圆柱；图②是圆锥．

[错因分析]　不能只依据概念的某一结论去判断．

[思路分析]　判断几何体的形状时，要考虑周全，要满足几何体的所有特征．

[正解]　图①不是圆柱，因为上下两面不平行(或不是由一个矩形旋转而成)；图②不是由一个直角三角形旋转而成，故不是圆锥．

X 　空间想象能力培养—卷与展

典例5 一圆柱的底半径为，母线长为4，轴截面为ABCD，从点A拉一绳子沿圆柱侧面到相对顶点C，求最短绳长.

[分析]　绳子沿圆柱侧面由A到C且最短，故侧面展开后为A，C两点间的线段长．

[解析]　沿BC剪开，将圆柱体的侧面的一半展开得到矩形BADC．则AD＝4，AB＝·π＝3．

∴AC＝＝5，即最短绳长为5．

『规律方法』　1.一般地，沿多面体或旋转体的表面最短距离(路程)问题，用侧面展开解决．

2．注意多面体、旋转体侧面(表面)的不同展开方法．

K

1．圆锥的母线有 (　D　)

A．2条　　 B．3条　　

C．4条　　 D．无数条

[解析]　圆锥的顶点与其底面圆上任意一点的连线都是圆锥的母线．

2．圆柱的母线长为10，则其高等于 (　B　)

A．5  B．10

C．20  D．不确定

[解析]　圆柱的母线长与高相等，则其高等于10．

3．圆台的母线 (　B　)

A．平行  B．相等

C．与高相等  D．与底面平行

[解析]　圆台的母线延长线交于一点，则A项不正确；圆台的母线大于高，则C项不正确；圆台的母线与底面相交，则D项不正确；很明显B项正确．

4．已知圆锥SO的母线长为5，底面直径为8，则圆锥SO的高h＝__3__.

[解析]　如图

∵圆锥的底面直径AB＝8

∴圆锥的底面半径R＝OA＝4

又∵SA＝5

∴圆锥的高h＝SO＝＝3．