初中数学华师大版八年级下册18.1 平行四边形的性质评课ppt课件

这是一份初中数学华师大版八年级下册18.1 平行四边形的性质评课ppt课件，共18页。PPT课件主要包含了复习引入，猜一猜，怎样证明这个猜想呢，证一证，应用格式，归纳总结，∴OEOF，再变一变，练一练，又∵AC⊥BC等内容，欢迎下载使用。

问题：上节课我们学习了平行四边形的哪些性质？
平行四边形的对边相等.
平行四边形的对角相等.
思考：平行四边形除了以上边和角的特征，其对角线有什么特征呢？这节课我们一起探讨一下吧.
平行四边形的邻角互补.
我们知道平行四边形的边角这两个基本要素的性质，那么平行四边形的对角线又具有怎样的性质呢?
如图，在□ABCD中，连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
OA=OC,OB=OD
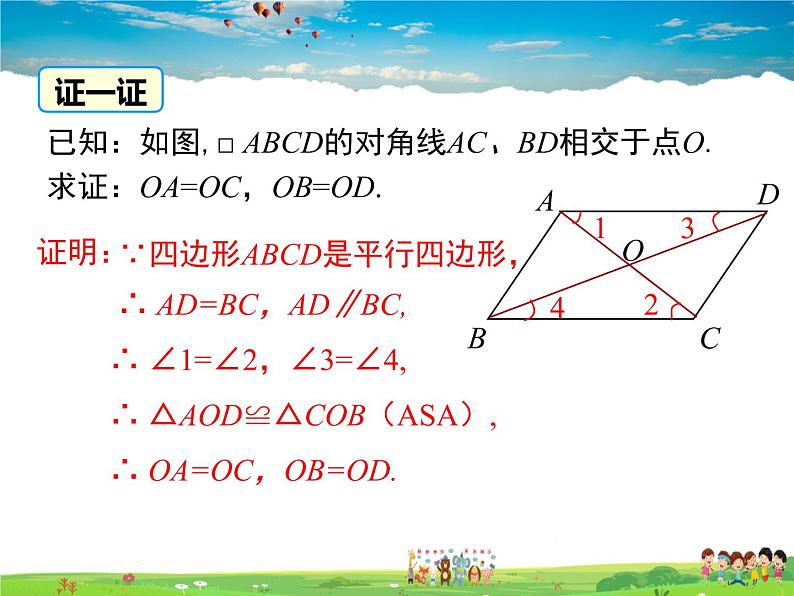
已知：如图,□ ABCD的对角线AC、BD相交于点O.求证：OA=OC，OB=OD.
∵四边形ABCD是平行四边形，
∴ AD=BC，AD∥BC,
∴ ∠1=∠2，∠3=∠4,
∴ △AOD≌△COB（ASA）,
∴ OA=OC，OB=OD.
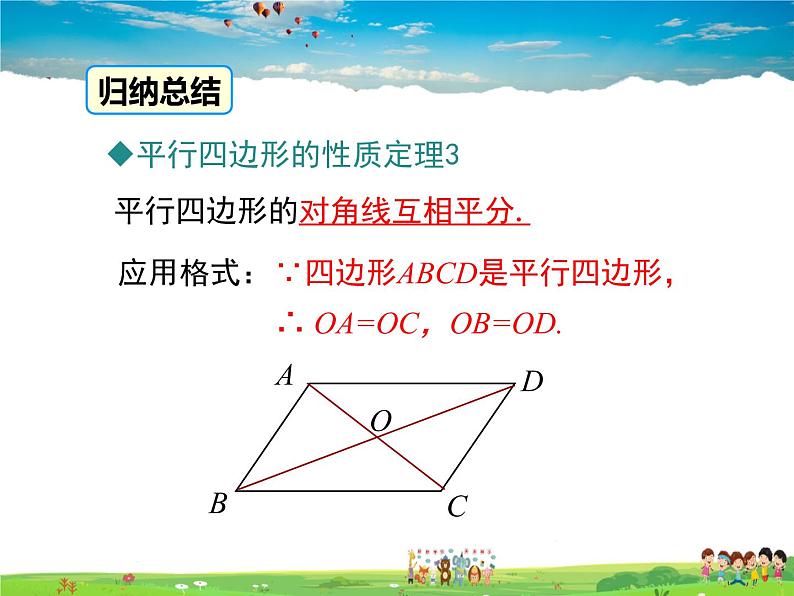
平行四边形的对角线互相平分.
平行四边形的性质定理3
例1 如图,平行四边形ABCD中，AC、BD交于O点，点E、F分别是AO、CO的中点，试判断线段BE、DF的关系并证明你的结论．
解：BE＝DF，BE∥DF.理由如下：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD,∴OE＝OF.在△OFD和△OEB中，OF＝OE，∠DOF＝∠BOE，OD＝OB， ∴△OFD≌△OEB，∴∠OEB＝∠OFD，BE＝DF，∴BE∥DF.
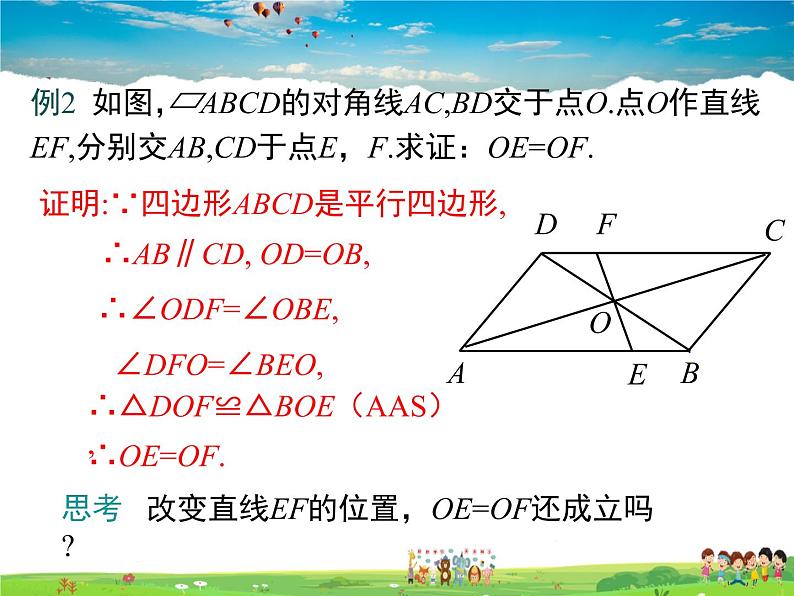
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE, ∠DFO=∠BEO,
∴△DOF≌△BOE（AAS）,
∴AB∥CD, OD=OB,
思考 改变直线EF的位置，OE=OF还成立吗?
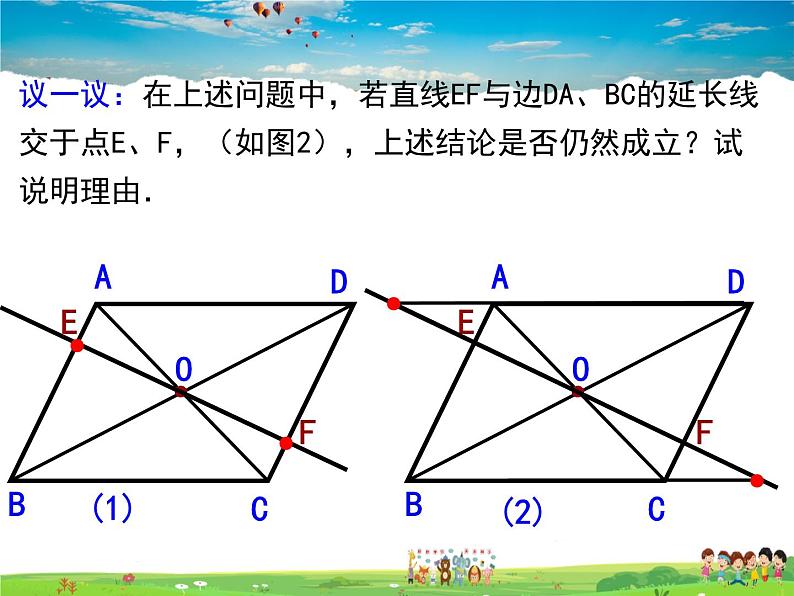
议一议：在上述问题中，若直线EF与边DA、BC的延长线交于点E、F，（如图2），上述结论是否仍然成立？试说明理由．
议一议：在上述问题中，若将直线EF绕点O旋转至下图(3)、(4)的位置时，上述结论是否仍然成立？
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交，得到的线段总相等．
1.如图，平行四边形ABCD的对角线AC，BD交于点O，若AD=16，AC=24，BD=12，则△OBC的周长为 （　　） A.26 B.34 C.40 D.52
2.如图，在▱ABCD中，对角线AC和BD相交于点O，△AOB的周长为15，AB=6，则对角线AC、BD的长度的和是 （　　）A.9 B.18 C.27 D.36
1.如图，在平行四边形ABCD中，下列结论中错误的是（　　）A．∠ABO=∠CDO B．∠BAD=∠BCD C．AO=CO D．AC⊥BD
2.在□ABCD中，AC=24,BD=38,AB=m, 则m的取值范围是 ( ) A. 243.如图，平行四边形ABCD中，对角线AC、BD相交于点O，AB⊥AC，AB=3，AD=5，则BD的长是 .
4.如图，四边形ABCD是平行四边形，AB=10，AD=8，AC⊥BC，求BC、CD、AC、OA的长.
∴△ABC是直角三角形.
∴BC=AD=8，CD=AB=10
∵四边形ABCD是平行四边形.
5. 如图，平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点，连接BE,DF. 求证:BE=DF.
证明： ∵四边形ABCD是平行四边形，对角线AC、BD交于点O,
∴OB=OD,OA=OC.
∵E,F分别是OA,OC的中点,