华师大版八年级下册第18章 平行四边形18.1 平行四边形的性质习题ppt课件

这是一份华师大版八年级下册第18章 平行四边形18.1 平行四边形的性质习题ppt课件，共25页。PPT课件主要包含了＜m＜11等内容，欢迎下载使用。

知识点1：平行四边形的对角线互相平分1．在▱ABCD中，对角线AC、BD相交于点O，则下列结论一定成立的是( )A．AC⊥BD B．OA＝OCC．AC＝BD D．AO＝OD
2．如图，EF过▱ABCD的对角线的交点O，交AD于点E，交BC于点F，若AB＝4，BC＝5，OE＝1.5，那么四边形EFCD的周长是( )A．16B．14C．12D．10
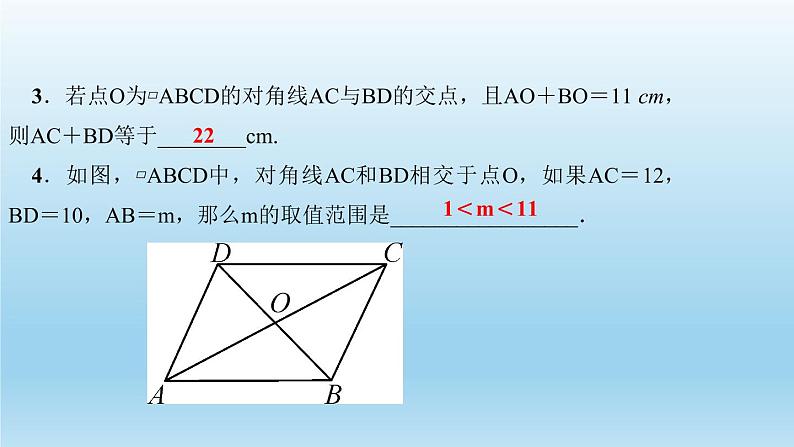
3．若点O为▱ABCD的对角线AC与BD的交点，且AO＋BO＝11 cm，则AC＋BD等于________cm.4．如图，▱ABCD中，对角线AC和BD相交于点O，如果AC＝12，BD＝10，AB＝m，那么m的取值范围是_________________．
5．如图，在▱ABCD中，AC、BD相交于点O，AB＝10 cm，AD＝8 cm，AC⊥BC，则OB＝____________cm.
6．如图，在▱ABCD中，AC与BD相交于点O，AB⊥AC，∠DAC＝45°，AC＝2.求BD的长．
知识点2：平行四边形的中心对称性7．如图，▱ABCD中，AC、BD为对角线，BC＝6，BC边上的高为4，则图中阴影部分的面积为( )A．3 B．6 C．12 D．24
8．某广场上有一个形状是平行四边形的花坛ABCD(如图)，里面分别种有红、黄、蓝、绿、橙、紫6种颜色的花，如果有AB∥EF∥DC，BC∥GH∥AD，那么下列说法中错误的是( )A．红花、绿花的种植面积一定相等B．紫花、橙花的种植面积一定相等C．红花、蓝花的种植面积一定相等D．蓝花、黄花的种植面积一定相等
9．平行四边形的对角线把平行四边形分成的4个小三角形的面积______________．
易错点：未充分利用平行四边形的性质10．在平行四边形ABCD中，AC与BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，则图中的全等三角形共( )A．5对B．6对C．7对D．8对
11．如图，在▱ABCD中，∠ODA＝90°，AC＝10 cm，BD＝6 cm，则AD的长为( )A．4 cm B．5 cm C．6 cm D．8 cm
12．如图，▱ABCD的对角线交于点O，且AB＝5，△OCD的周长为23，则▱ABCD的两条对角线的和是( )A．18 B．28 C．36 D．46
13．一个平行四边形的三个顶点坐标分别是(0，0)，(2，0)，(1，2)，第四个顶点在x轴下方，则第四个顶点的坐标为( )A．(－1，－2) B．(1，－2)C．(3，2) D．(－1，2)
14．(导学号19414080)如图，在周长为20 cm的▱ABCD中，AB≠AD，AC、BD相交于点O，OE⊥BD交AD于点E，则△ABE的周长为_____________．
15．(导学号19414081)如图所示，在▱ABCD中，对角线AC、BD相交于点O，过点O的直线分别交AD、BC于点M、N，若△CON的面积为2，△DOM的面积为4，则△AOB的面积为________．
16．如图，已知点A(－4，2)，B(－1，－2)，平行四边形ABCD的对角线交于坐标原点O.(1)求点C、D的坐标；(2)写出从线段AB到线段CD的变换过程；(3)求平行四边形ABCD的面积．
解：(1)∵四边形ABCD是平行四边形，且对角线交于坐标原点O，∴四边形ABCD关于O中心对称，∵A(－4，2)，B(－1，－2)，∴C(4，－2)，D(1，2)．(2)将线段AB绕点O旋转180°到线段CD.(3)点A到y轴的距离为4，点D到y轴的距离为1，A到x轴的距离为2，点B到x轴的距离为2，∴S平行四边形ABCD＝(1＋4)×(2＋2)＝20.
17．(导学号19414082)如图，▱ABCD的对角线AC、BD相交于点O，EF过点O且与AB、CD分别相交于点E、F，连结EC.(1)求证：OE＝OF；(2)若EF⊥AC，△BEC的周长是10，求▱ABCD的周长．
18．(导学号19414083)如图，▱ABCD中，E是AD的中点，连结BE并延长，交CD的延长线于点F.连结CE.(1)求证：△ABE≌△DFE；(2)当CE平分∠BCD时，猜想△BCF的形状，并说明理由．