





- 9.苏教版四下第七单元 平行四边形和梯形练习课件PPT 课件 11 次下载
- 10.苏教版四下第七单元 整理与练习课件PPT 课件 11 次下载
- 1.苏教版四下第八单元 用数对表示物体位置课件PPT 课件 10 次下载
- 2.苏教版四下第八单元 用数对表示点的位置课件PPT 课件 10 次下载
- 3.苏教版四下第八单元 整理与练习课件PPT 课件 9 次下载
苏教版四年级下册多边形的内角和图文ppt课件
展开1.使学生经历提出问题、自主探索、观察分析、归纳概括等活动,了解多边形与它最少能分成三角形个数之间的关系,能正确计算多边形的内角和。 2.使学生经历探索、发现规律的过程,加深感受探索数学规律的一般方法,积累相应的数学活动经验,提高解决问题的能力。3.使学生主动参与活动过程,进一步产生对数学的好奇和自信。
【重点】探索多边形内角和的规律。
【难点】获得规律探究的一般方法。
请在书本第112的方格图中设计一个你喜欢的图案,再简单交代一下你希望如何平移,最后交给你的同桌,互相挑战一下吧!
同学们,关于三角形的内角和的学习过程你还有印象吗?想一想。今天我们要继续研究多边形的内角和,什么是多边形呢?多边形的内角和又该怎样来求得呢?小组讨论,交流交流吧!
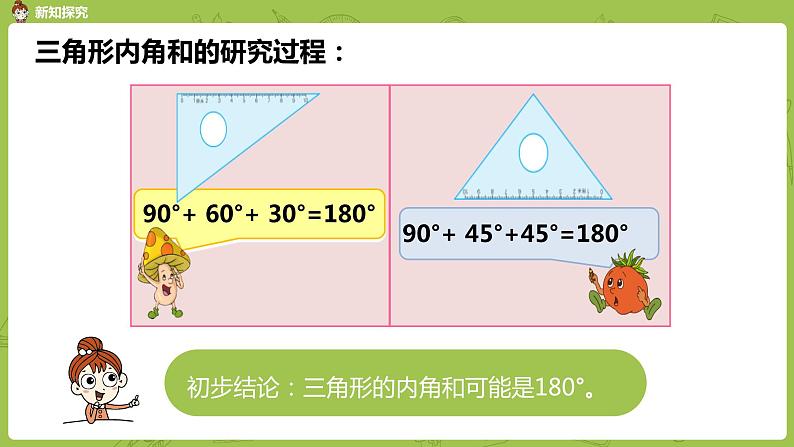
三角形内角和的研究过程:
90°+ 45°+45°=180°
90°+ 60°+ 30°=180°
初步结论:三角形的内角和可能是180°。
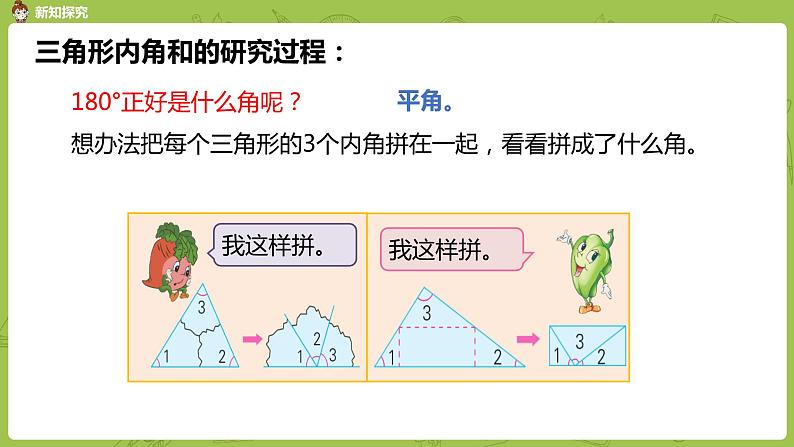
180°正好是什么角呢?想办法把每个三角形的3个内角拼在一起,看看拼成了什么角。
由三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。除了三角形,有几条边就叫几边形。
借鉴三角形内角和的研究方法:
我们量出三角形的内角和是180°,量一量四边形的内角和试试看,是不是也有什么规律,并试试看能不能验证自己的想法吧!
先量出每个角的度数,再求和。是360°。
把四边形分成2个三角形,算出内角和是360°。
接下来,五边形你准备怎么研究呢?六边形呢?量一量,分一分吧!
你得到结果了吗?是不是五边形540°、六边形720°?量的话,会有一些误差,所以我们在后续的研究中更加倾向于分割、计算!
六边形可以分成4个三角形。
五边形可以分成3个三角形。
其他多边形也可以像这样分成几个三角形来计算内角和吗?小组合作,任意画出一些多边形,试一试。
180°×3=540°
180°×4=720°
把请把你们小组的研究数据填入下表。
观察表中的数据,你有什么发现?能用一两句话总结吗?
分成的三角形个数都比多边形的边数少2。
可以把多边形分成若干个三角形,计算它的内角和。
分成了几个三角形,多边形的内角和就有几个180°。
你能用一个式子表示多边形内角和的计算方法吗?
(边数-2)×180 °
回顾探索和发现规律的过程,说说你的体会。
可以把新的问题转化成能够解决的问题。
从简单的问题想起、有序思考,是探索规律的有效方法。
多边形的内角和可以根据三角形的内角和推算出来。
1、一个三角形的内角和等于( )°。2、从四边形的一个顶点出发,可以引出( )条对角线,对角线将四边形分割成( )三角形。所以四边形的内角和是( )°。
计算多边形的内角和时,分割成三角形一定要注意是从一个顶点出发哦!
通过列式计算,快速得出八边形的内角和。
(8-2)x180°=1080°答:八边形的内角和是1080°。
100以内数的连减方法:按从左到右的顺序减,也可以先把后两个数相加,再用第一个数减去相加的结果。
借鉴三角形内角和的研究方法,我们研究出了多边形的内角和。最后通过总结,发现可以把三角形以外的其他多边形分成几个三角形,再来计算内角和。多边形内角和=(边数-2)×180 °。
每条边都相等的多边形我们称之为“正多边形”。正多边形的每个内角都相等,比如正三角形的每个内角都是60°,那么,正六边形的内角和是多少度呢?
(6-2)x180°=720°答:正六边形的内角和是720°(正六边形也是六边形)。
每条边都相等的多边形我们称之为“正多边形”。正多边形的每个内角都相等,比如正三角形的每个内角都是60°,那么,正六边形的每个内角是多少度呢?
(6-2)x180°=720°720°÷6=120°答:正六边形的每个内角都是120°。
照样子,算一算正五边形的每个内角是多少度?
(5-2)x180°=540°540°÷5=108°答:正五边形的每个内角都是108°。
已知一个四边形,它的三个角分别是90°、72°、83°,你知道它的另外一个角是多少度吗?
(4-2)x180°=360°360°-90°-72°-83°=115°答:它的另一个角是115°。
四年级下册三角形的内角和教学课件ppt: 这是一份四年级下册三角形的内角和教学课件ppt,文件包含人教版四下56《多边形的内角和》PPT课件pptx、人教版四下56《多边形的内角和》教学设计docx、人教版四下56《多边形的内角和》同步练习docx等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
数学四年级下册多边形的内角和一等奖课件ppt: 这是一份数学四年级下册多边形的内角和一等奖课件ppt,共10页。
2021学年多边形的内角和教案配套课件ppt: 这是一份2021学年多边形的内角和教案配套课件ppt,共19页。PPT课件主要包含了比一比,又称为多边形,探究新知,问题1,猜一猜,问题2,什么叫正多边形,问题3,做一做,问题4等内容,欢迎下载使用。














