2020-2021学年5.3.1 等比数列教学演示课件ppt

这是一份2020-2021学年5.3.1 等比数列教学演示课件ppt，共31页。PPT课件主要包含了一个格子里麦粒数的，且共有，麦粒总数，①②得，错位相减法，q≠1，等比数列前n项公式，当q1时，判断是非，公式运用等内容，欢迎下载使用。

2.5 等比数列前n项和公式
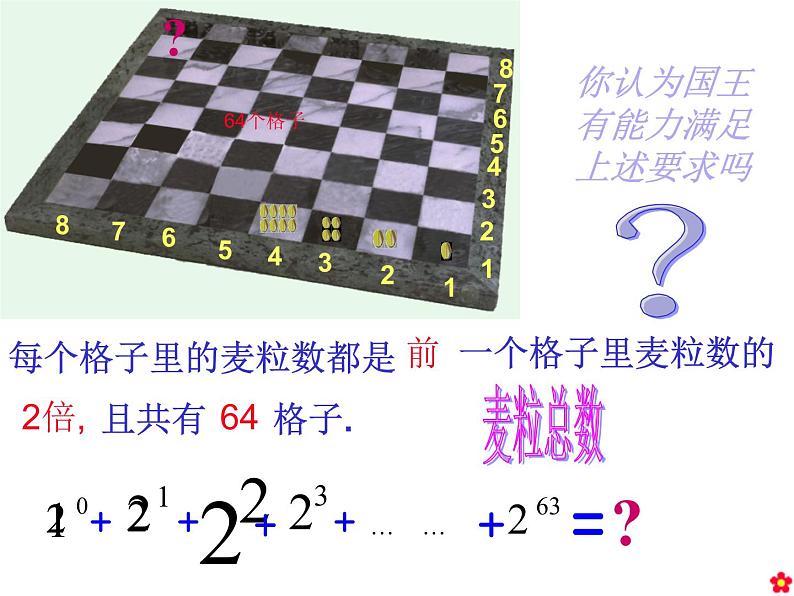
你认为国王有能力满足上述要求吗
每个格子里的麦粒数都是
由刚才的例子可知：实际上就是一个以1为首项，2为公比的等比数列的前64项的求和问题，即：
所以当人们把一袋一袋的麦子搬来开始计数时，国王才发现：就是把全印度甚至全世界的麦粒全拿来，也满足不了他的要求。
其实，人们估计，全世界一千年也难以生产这么多麦子!是当时全世界在两千年内所产的小麦的总和！
假定千粒麦子的质量为40g,那么麦粒的总质量超过了7000亿吨。
如果造一个宽四米，高四米的粮仓来储存这些粮食，那么这个粮仓就要长三亿千米，可以绕地球赤道7500圈，或在太阳和地球之间打个来回。
思考：（1）为什么②式选择乘以2，而不是别的数字？乘以2有什么样的好处？（2）类比以上例子，你能发现什么规律？
如何求等比数列的Sn:
等比数列前n项和公式的推导
思考：那q=1怎么办呢？提示：q=1说明数列有什么特点？
2.推导公式的方法：错位相减法。
是等比数列，请完成下表：
a1、q、n、an、Sn中
求数列 的前n项的和.
例2.某商场今年销售计算机5000台，如果平均每年的销售量比上一年的销售量增加10%，那么从今起，大约几年可使总销售量达到30000台(结果保留到个位)？
分析：第1年产量为 5000台
5000×(1+10%)=5000×1.1台
5000×(1+10%) ×(1+10%)
例2.某商场第一年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位)?
答:约5年内可以使总销售量达到30000台.
思考：已知一等比数列{an},其项数为偶数，其所有奇数项的和为S奇=100 ，公比q=2，求其所有偶数项的和S偶。
这数列里面的任何一项都不能为0！