初中数学华师大版九年级上册24.2直角三角形的性质图文课件ppt

这是一份初中数学华师大版九年级上册24.2直角三角形的性质图文课件ppt，共20页。PPT课件主要包含了矩形的判定，温故知新，∴ADDB，又∵CDDE，∵∠ACBRt∠，矩形的对角线相等，∴CEAB，∴∠ACB90°，还有其它证法吗，练一练等内容，欢迎下载使用。

定理1：有三个角是直角的四边形是矩形
定理2：对角线相等的平行四边形是矩形
有一个角是直角的平行四边形叫是矩形
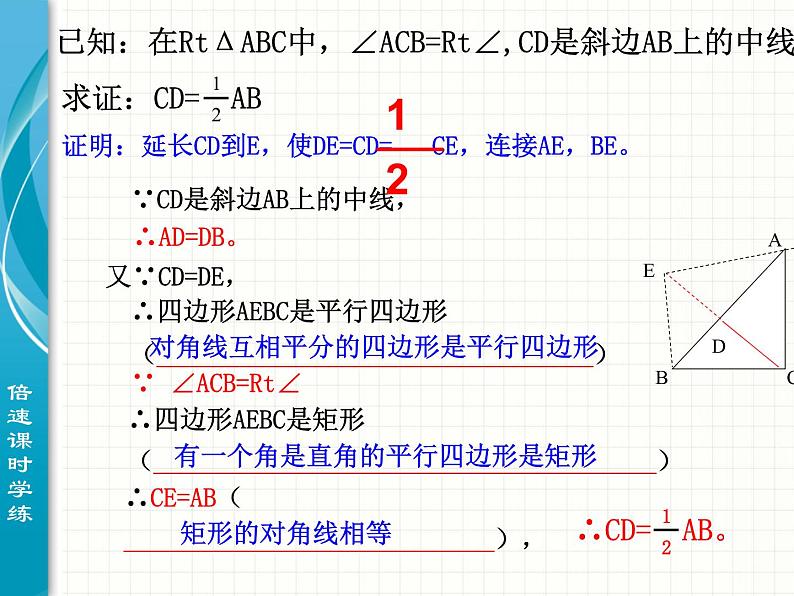
已知：在RtΔABC中，∠ACB=Rt∠,CD是斜边AB上的中线
证明：延长CD到E，使DE=CD= CE，连接AE，BE。
∵CD是斜边AB上的中线，
∴四边形AEBC是平行四边形（_________________________________）
∴CE=AB（____________________________），
∴四边形AEBC是矩形（______________________________________）
对角线互相平分的四边形是平行四边形
有一个角是直角的平行四边形是矩形
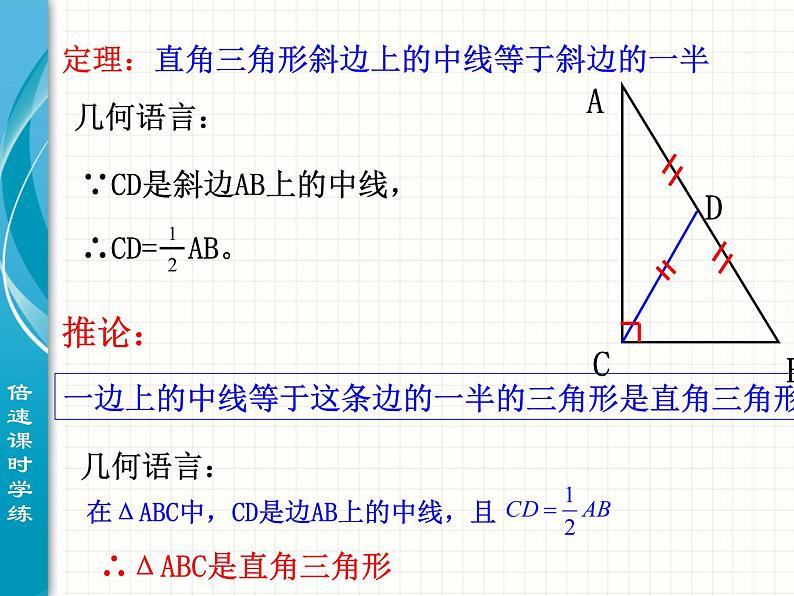
一边上的中线等于这条边的一半的三角形是直角三角形
求证： ΔABC是直角三角形
∵CD是边AB上的中线，
∴四边形AEBC是平行四边形
∴四边形AEBC是矩形
（对角线相等的平行四边形是矩形）
∴△ABC是直角三角形
定理：直角三角形斜边上的中线等于斜边的一半
∴ΔABC是直角三角形
1、证明一条线段是另一条线段的1/2或2倍，常用的定理：“三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半”
2、添辅助线的方法：延长短的使它等于原来的，再证相等；或在长的上截取一段使它等于短，再证中点。
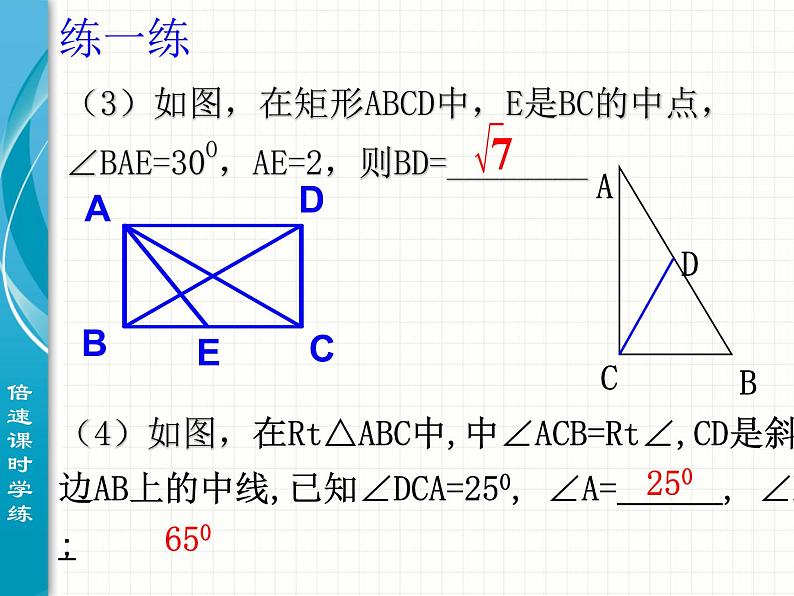
（3）如图，在矩形ABCD中，E是BC的中点，∠BAE=30O，AE=2，则BD=________
（4）如图，在Rt△ABC中,中∠ACB=Rt∠,CD是斜边AB上的中线,已知∠DCA=250, ∠A= , ∠B= ;
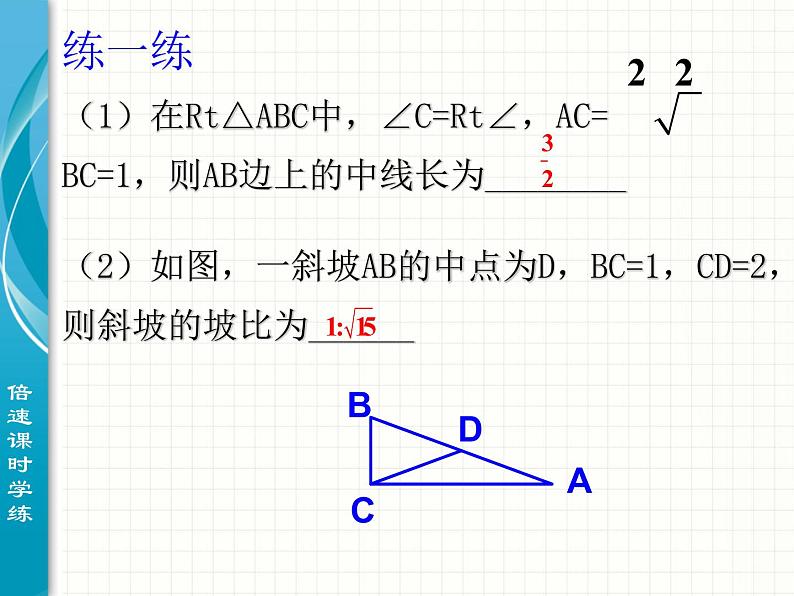
（5）如图，已知BC=20m， ∠B=∠C=30°， E、G分别为AB，AC的中点，P为BC的中点，且EF⊥BC， GH⊥BC，垂足分别为F，H，求EF、PG的长；
（6）一张平行四边形纸片如图。现要求剪一刀，把它分成两部分，然后做适当的图形变换，把剪开的两部分拼成一个矩形，说明你的剪法和所采用的变换。
例、求证：在直角三角形中，300角所对直角边等于斜边的一半。
已知：在RtΔABC中，∠ACB=Rt∠, ∠A= 30°
在直角三角形中，等于斜边一半的直角边所对的角等于30°
已知：在RtΔABC中，∠ACB=Rt∠,
求证：∠A= 30°
说明：上面两个性质只能局限于填空和选择题
例1、已知：如图，△ABC中，BD，CE是高，G、F分别是BC，DE的中点。试判断FG与DE的位置关系，并加以证明。
变式：已知：如图，在四边形ABCD中，∠ABC= ∠ADC=Rt∠，M是AC的中点，N是BD的中点。试判断MN与BD的位置关系，并加以证明。
1、如图Ｒt⊿ABC中，∠ＡＣＢ＝９０°，点Ｄ，Ｆ分别是ＡＣ，ＢＣ边上的中点，点Ｅ是ＡＢ边上的中点，如果ＣＥ＝３，则ＤＦ＝＿＿＿
∵点Ｅ是ＡＢ边上的中点，∠ＡＣＢ＝９０°
∴ＣＥ是Ｒt⊿ABC的斜边的中线
∴ＡＢ＝２ＣＥ＝２×３＝６（＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
直角三角形的斜边的中线等于斜边的一半）
∵点Ｄ，Ｆ分别是ＡＣ，ＢＣ边上的中点，
∴DF是三角形ＡＢＣ的中位线
(三角形的中位线等于第三边的一半）
2、 如图：在RtΔABC中，CD是斜边AB上的中线，已知∠DCA=200，则∠ A ＝＿＿，∠B＝____。
∵CD是斜边AB上的中线
∴CD=AD=BD= AB(直角三角形的斜边中线等于斜边的一半）
∴∠Ａ＝∠ＤＣＡ＝２０°
∴∠Ｂ＝９０°－ ∠Ａ＝ ９０°－２０°＝７０°（直角三角形两锐角互余）
3、在矩形ABCD中，E是BC上一点，已知AE=AD,DF垂直与AE于点F,求证：CE=FE
4、以ᇫABC的三边在BC 的同侧分别作三个等边三角形，即ᇫABC,ᇫBCE,ᇫACF,请回答下列问题：
（1）四边形ADEF是什么四边形？
（2）当ᇫABC满足什么条件时，四边形ADEF是矩形？