2018-2019学年广东省东莞市七下期中数学试卷

这是一份2018-2019学年广东省东莞市七下期中数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 16 的算术平方根是
A. 8B. −8C. 4D. ±4

2. 点 P2,−3 所在的象限为
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

3. 在实数 −23，π，3，−3.14，4 中无理数的个数是
A. 1B. 2C. 3D. 4

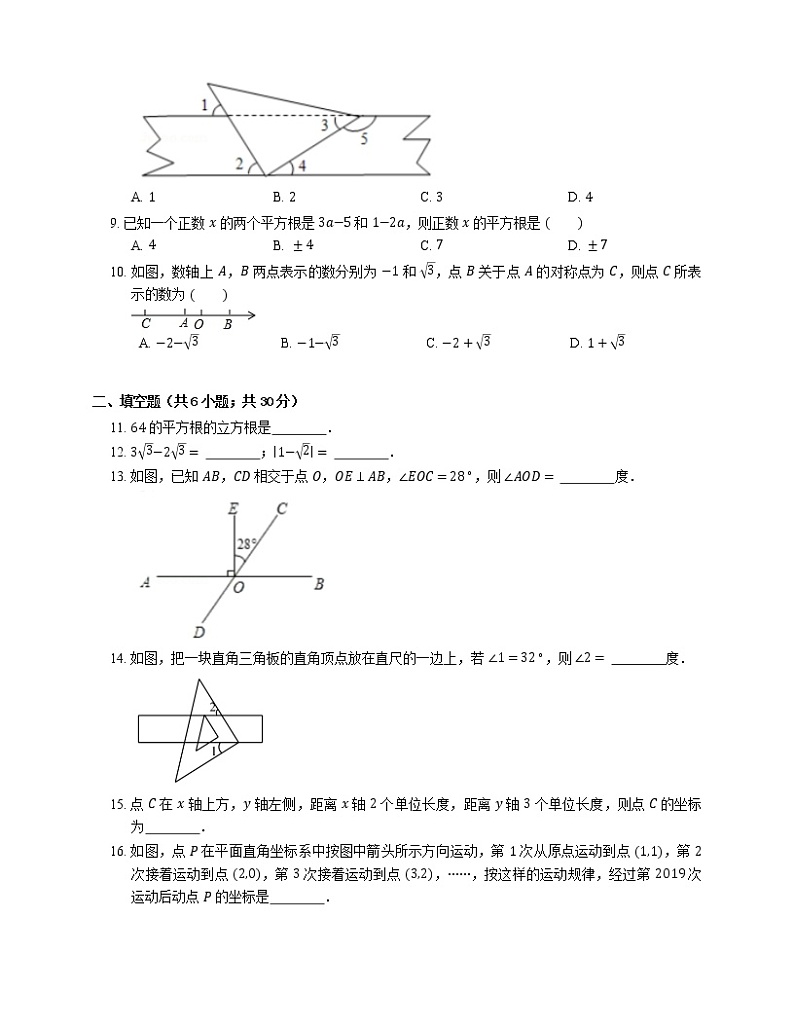
4. 如图，下列不能判定 AB∥CD 的条件是
A. ∠B+∠BCD=180∘B. ∠1=∠2
C. ∠3=∠4D. ∠B=∠5

5. 若 x 轴上的点 P 到 y 轴的距离是 3，则点 P 的坐标为
A. 3,0B. 3,0 或 −3,0
C. 3,0D. 0,3 或 0,−3

6. 下列命题是真命题的是
A. 内错角相等
B. 同位角相等，两直线平行
C. 一个角的余角不等于它本身
D. 在同一平面内，有且只有一条直线与已知直线垂直

7. 估算 27−2 的值
A. 在 1 到 2 之间B. 在 2 到 3 之间
C. 在 3 到 4 之间D. 在 4 到 5 之间

8. 将一直角三角板与两边平行的纸条如图所示放置，下列结论：
（1）∠1=∠2；
（2）∠3=∠4；
（3）∠2+∠4=90∘；
（4）∠4+∠5=180∘，
其中正确的个数是
A. 1B. 2C. 3D. 4

9. 已知一个正数 x 的两个平方根是 3a−5 和 1−2a，则正数 x 的平方根是
A. 4B. ±4C. 7D. ±7

10. 如图，数轴上 A，B 两点表示的数分别为 −1 和 3，点 B 关于点 A 的对称点为 C，则点 C 所表示的数为
A. −2−3B. −1−3C. −2+3D. 1+3

二、填空题（共6小题；共30分）
11. 64 的平方根的立方根是 ．

12. 33−23= ；1−2= ．

13. 如图，已知 AB，CD 相交于点 O，OE⊥AB，∠EOC=28∘，则 ∠AOD= 度．

14. 如图，把一块直角三角板的直角顶点放在直尺的一边上，若 ∠1=32∘，则 ∠2= 度．

15. 点 C 在 x 轴上方，y 轴左侧，距离 x 轴 2 个单位长度，距离 y 轴 3 个单位长度，则点 C 的坐标为 ．

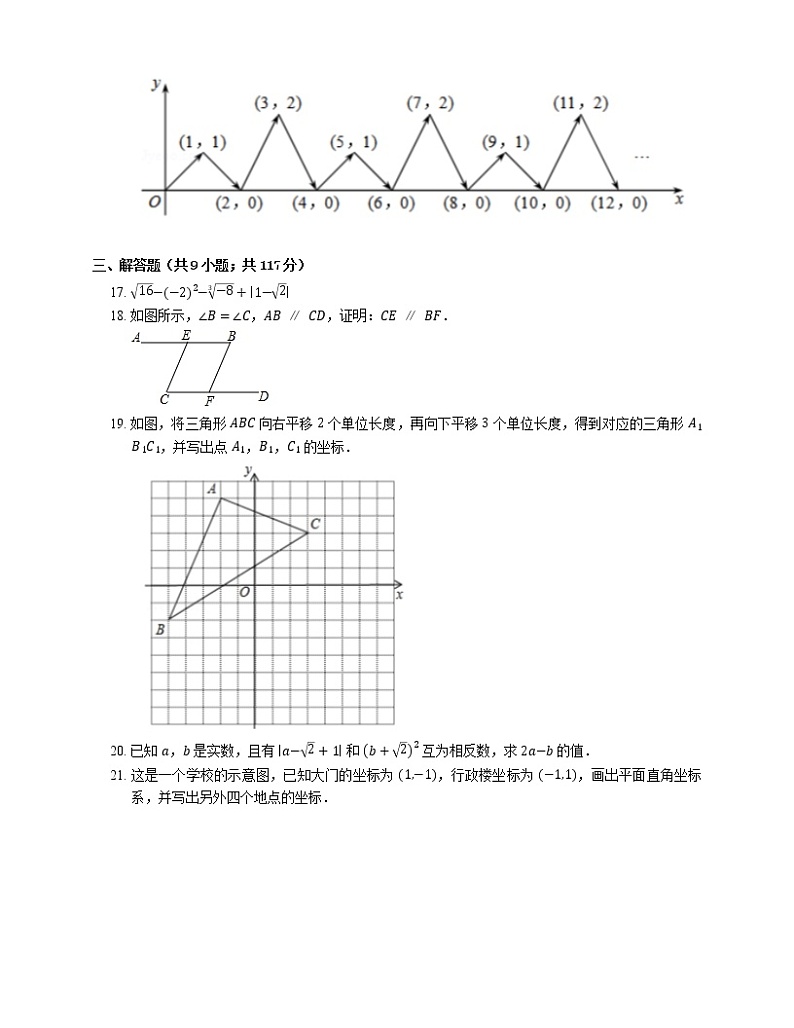
16. 如图，点 P 在平面直角坐标系中按图中箭头所示方向运动，第 1 次从原点运动到点 1,1，第 2 次接着运动到点 2,0，第 3 次接着运动到点 3,2，⋯⋯，按这样的运动规律，经过第 2019 次运动后动点 P 的坐标是 ．

三、解答题（共9小题；共117分）
17. 16−−22−3−8+1−2

18. 如图所示，∠B=∠C，AB∥CD，证明：CE∥BF．

19. 如图，将三角形 ABC 向右平移 2 个单位长度，再向下平移 3 个单位长度，得到对应的三角形 A1B1C1，并写出点 A1，B1，C1 的坐标．

20. 已知 a，b 是实数，且有 a−2+1 和 b+22 互为相反数，求 2a−b 的值．

21. 这是一个学校的示意图，已知大门的坐标为 1,−1，行政楼坐标为 −1,1，画出平面直角坐标系，并写出另外四个地点的坐标．

22. EF 交 AB 于 G，交 CD 于 F，FH 平分 ∠EFD，交 AB 于 H，∠EGH=130∘，∠EFC=50∘．
（1）求证：AB∥CD；
（2）求 ∠BHF 的度数．

23. 先观察下列各式：1=1；1+3=4=2；1+3+5=9=3；1+3+5+7=16=4．
（1）计算：1+3+5+7+9+11= ；
（2）已知 n 为正整数，通过观察并归纳，请写出：1+3+5+7+9+11+⋯+2n−1= ；
（3）应用上述结论，请计算 4+12+20+28+36+44+⋯+204 的值．

24. 如图，已知 ∠1+∠2=180∘，∠DEF=∠A，试判断 ∠ACB 与 ∠DEB 的大小关系，并证明．

25. 如图，已知 A−2,0，B4,0，C2,4，D0,2．
（1）求三角形 ABC 的面积；
（2）设 P 为坐标轴上一点，若 S△APC=12S△ABC，求 P 点的坐标．
答案
第一部分
1. C【解析】∵±42=16，
∴16 的算术平方根是4，
故选：C．
2. D【解析】∵ 点 P 的横坐标为正，纵坐标为负，
∴ 点 P2,−3 所在象限为第四象限．
3. B【解析】π，3 是无理数，故选：B．
4. B【解析】A．∵∠B+∠BCD=180∘，
∴AB∥CD，故不符合题意；
B．∵∠1=∠2，
∴AD∥BC，故符合题意；
C．∵∠3=∠4，
∴AB∥CD，故不符合题意；
D．∵∠B=∠5，
∴AB∥CD，故不符合题意．
5. B
【解析】∵x 轴上的点 P 到 y 轴的距离是 3，
∴ 点 P 的横坐标为 3 或 −3，纵坐标为 0，
∴ 点 P 的坐标为 3,0 或 −3,0．
6. B【解析】A、两直线平行，内错角相等，是假命题；
B、同位角相等，两直线平行，是真命题；
C、一个角的余角可以等于它本身，如 90∘ 角，是假命题；
D、在同一平面内，过一点有且只有一条直线与已知直线垂直，是假命题；
故选：B．
7. C【解析】∵5<27<6，
∴3<27−2<4．
8. D【解析】∵ 纸条的两边平行，
∴（1）∠1=∠2（同位角）；（2）∠3=∠4（内错角）；（4）∠4+∠5=180∘（同旁内角）均正确；
又 ∵ 直角三角板与纸条下线相交的角为 90∘，
∴（3）∠2+∠4=90∘，正确．
9. D【解析】根据题意知 3a−5+1−2a=0，
解得 a=4，
则正数 x 的平方根为 ±3a−5=±12−5=±7，
故选：D．
10. A
【解析】∵ 对称的两点到对称中心的距离相等，
∴CA=AB，−1+3=1+3，
∴OC=2+3，而 C 点在原点左侧，
∴C 表示的数为 −2−3．
第二部分
11. ±2
【解析】∵64 的平方根是 ±8，8 的立方根是 2，−8 的立方根是 −2，
∴64 的平方根的立方根是 ±2．
12. 3，2−1
【解析】33−23=3；
1−2=2−1．
13. 62
【解析】∵OE⊥AB，∠EOC=28∘，
∴∠COB=90∘−∠EOC=62∘，
∴∠AOD=62∘（对顶角相等）．
14. 58
【解析】如图，
∵AB∥CD，
∴∠2=∠3，
∵∠1+∠3=90∘，∠1=32∘，
∴∠2=∠3=90∘−32∘=58∘．
15. −3,2
【解析】∵ 点 C 在 x 轴上方，y 轴左侧，
∴ 点 C 在第二象限，
∵ 点 C 距离 x 轴 2 个单位长度，距离 y 轴 3 个单位长度，
∴ 点 C 的横坐标为 −3，纵坐标为 2，
∴ 点 C 的坐标为 −3,2．
16. 2019,2
【解析】分析图象可以发现，点 P 的运动每 4 次位置循环一次．每循环一次向右移动四个单位．
∴2019=4×504+3．
当第 504 循环结束时，点 P 位置在 2016,0，在此基础之上运动三次到 2019,2．
第三部分
17. 原式=4−4+2+2−1=1+2．
18. ∵AB∥CD，
∴∠AEC=∠C．
∵∠B=∠C，
∴∠AEC=∠B，
∴CE∥BF．
19. 作图如图，
各点坐标为：A10,2，B1−3,−5，C15,0．
20. 由题意得：a−2+1=0，b+2=0，
解得：a=2−1，b=−2，
则 2a−b=22−2+2=32−2．
21. 根据题意可建立如图所示平面直角坐标系，
由图可知图书馆的坐标为 5,1，教学楼的坐标为 1,3，
实验楼的坐标 −1,5，食堂的坐标为 4,7．
22. （1） ∵∠EGH=130∘，∠EFC=50∘，
∴∠EGH+∠EFC=180∘．
∵∠EGH+∠EGA=180∘，
∴∠EFC=∠EGA，
∴AB∥CD．
（2） ∵∠EFC+∠EFD=180∘，∠EFC=50∘，
∴∠EFD=130∘．
∵FH 平分 ∠EFD，
∴∠HFD=12∠EFD=65∘．
∵AB∥CD，
∴∠BHF=180∘−∠HFD=115∘．
23. （1） 6
【解析】1+3+5+7+9+11=36=6．
（2） n
【解析】1+3+5+7+9+11+⋯+2n−1=n2=n．
（3） 4+12+20+28+36+44+⋯+204=4×1+3+5+⋯+51=4×262=2×26=52.
24. ∠ACB 与 ∠DEB 相等，理由如下：
证明：
∵∠1+∠2=180∘（已知），∠1+∠DFE=180∘（邻补角定义），
∴∠2=∠DFE（同角的补角相等），
∴AB∥EF（内错角相等两直线平行），
∴∠BDE=∠DEF（两直线平行，内错角相等），
∵∠DEF=∠A（已知），
∴∠BDE=∠A（等量代换），
∴DE∥AC（同位角相等两直线平行），
∴∠ACB=∠DEB（两直线平行，同位角相等）．
25. （1） ∵A−2,0，B4,0，C2,4，
∴AB=2+4=6，
∴S△ABC=12×4+2×4=12．
（2） 当 P 在 x 轴上时，设 P 点坐标为 m,0，
12m+2×4=12×12，解得 m1=1，m2=−5；
当 P 在 y 轴上时，设 P 点坐标为 0,n，
∵D0,2，
∴PD=n−2，
∴12n−2×2+2=12×12，解得 n1=−1，n2=5．
∴P 点坐标为 −5,0 或 1,0 或 0,−1 或 0,5．