2018-2019学年广东省佛山市南海区丹灶镇初级中学七下期中数学试卷

这是一份2018-2019学年广东省佛山市南海区丹灶镇初级中学七下期中数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列计算中，正确的是
A. a23=a5B. a2⋅a3=a6C. 2a⋅3a=6a2D. 2a+3a=5a2

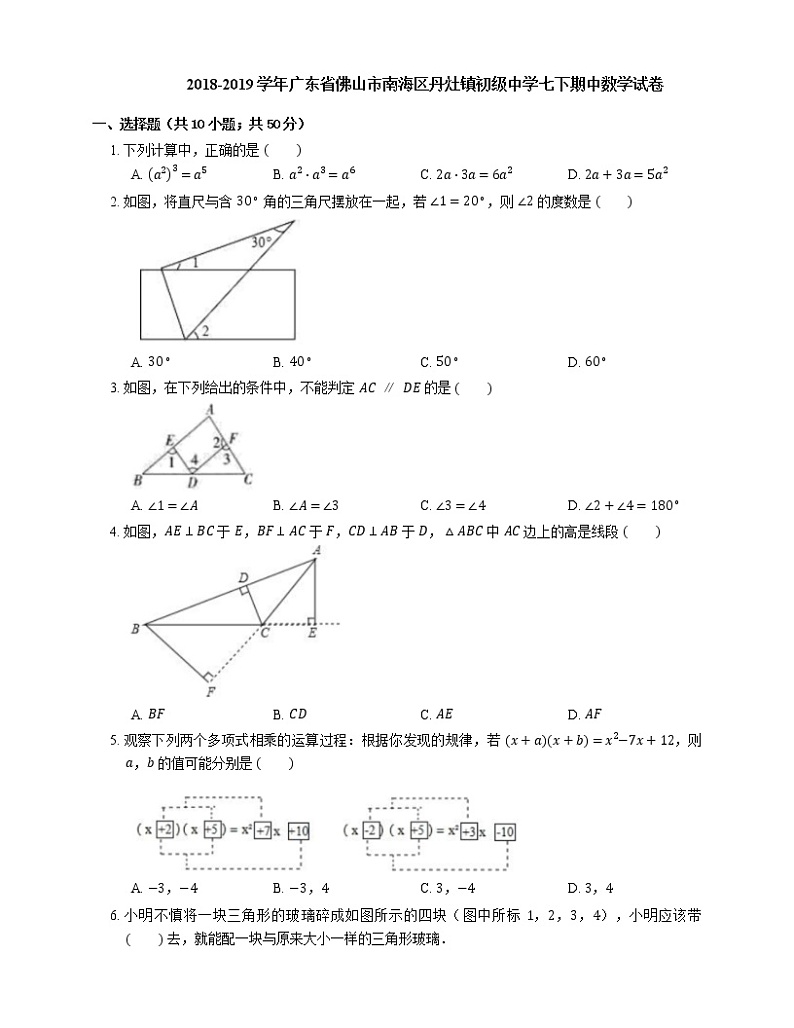
2. 如图，将直尺与含 30∘ 角的三角尺摆放在一起，若 ∠1=20∘，则 ∠2 的度数是
A. 30∘B. 40∘C. 50∘D. 60∘

3. 如图，在下列给出的条件中，不能判定 AC∥DE 的是
A. ∠1=∠AB. ∠A=∠3C. ∠3=∠4D. ∠2+∠4=180∘

4. 如图，AE⊥BC 于 E，BF⊥AC 于 F，CD⊥AB 于 D，△ABC 中 AC 边上的高是线段
A. BFB. CDC. AED. AF

5. 观察下列两个多项式相乘的运算过程：根据你发现的规律，若 x+ax+b=x2−7x+12，则 a，b 的值可能分别是
A. −3，−4B. −3，4C. 3，−4D. 3，4

6. 小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标 1，2，3，4），小明应该带 去，就能配一块与原来大小一样的三角形玻璃．
A. 第 1 块B. 第 2 块C. 第 3 块D. 第 4 块

7. 用 100 元钱在网上书店恰好可购买 m 本书，但是每本书需另加邮寄费 6 角，购买 n 本书共需费用 y 元，则可列出关系式
A. y=n100m+0.6B. y=n100m+0.6
C. y=n100m+0.6D. y=100mn+0.6

8. 如图，点 B，E，C，F 在同一条直线上，AB∥DE，AB=DE，要用 SAS 证明 △ABC≌△DEF，可以添加的条件是
A. ∠A=∠DB. AC∥DFC. BE=CFD. AC=DF

9. 若 a，b，c 是正数，下列各式，从左到右的变形不能用如图验证的是
A. b+c2=b2+2bc+c2
B. ab+c=ab+ac
C. a+b+c2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=aa+2b

10. 如图，在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 CEFG，动点 P 从 A 出发，沿 A→D→E→F→G→B 的路线绕多边形的边匀速运动到点 B 时停止（不含点 A 和点 B），则 △ABP 的面积 S 随着时间 t 变化的函数图象大致为
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 计算 2x2y2÷xy 的结果是 ．

12. 如图，∠1=∠2，需增加条件 可以使得 AB∥CD（只写一种）．

13. 在 △ABC 中，∠A=60∘，∠B=2∠C，则 ∠B= ∘．

14. 某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：
鸭的质量/千克烤制时间/分6080100120140160180
设鸭的质量为 x 千克，烤制时间为 t，估计当 x=2.9 千克时，t 的值为 ．

15. 如图，两根旗杆间相距 12 m，某人从点 B 沿 BA 走向点 A，一段时间后他到达点 M，此时他仰望旗杆的顶点 C 和 D，两次视线的夹角为 90∘，且 CM=DM，已知旗杆 AC 的高为 3 m，该人的运动速度为 1 m/s，则这个人运动到点 M 所用时间是 ．

16. 如图，两个正方形边长分别为 a，b，如果 a+b=20，ab=18，则阴影部分的面积为 ．

三、解答题（共9小题；共117分）
17. 计算：−12019+13−2−3.14−π0．

18. 先化简，再求值：2x−y2x+y−4x−yx+y，其中 x=13，y=−2．

19. 已知：线段 a，∠α，∠β．求作：△ABC，使 BC=a，∠B=∠α，∠C=∠β．

20. 已知：如图，∠A=∠ADE，∠C=∠E．
（1）若 ∠EDC=3∠C，求 ∠C 的度数；
（2）求证：BE∥CD．

21. 如图，AB=AD，AC=AE，BC=DE，点 E 在 BC 上．
（1）求证：△ABC≌△ADE；
（2）求证：∠EAC=∠DEB．

22. 如图 1，在四边形 ABCD 中，AB∥CD，∠ABC=90∘，动点 P 从 A 点出发，沿 A→D→C→B 匀速运动，设点 P 运动的路程为 x，△ABP 的面积为 y，图象如图 2 所示．
（1）① AD= ，CD= ，BC= ；（填空）
②当点 P 运动的路程 x=8 时，△ABP 的面积为 y= ；（填空）
（2）求四边形 ABCD 的面积．

23. 如图，已知 AB∥CD，∠A=40∘．点 P 是射线 AB 上一动点（与点 A 不重合），CE，CF 分别平分 ∠ACP 和 ∠DCP 交射线 AB 于点 E，F．
（1）求 ∠ECF 的度数；
（2）随着点 P 的运动，∠APC 与 ∠AFC 之间的数量关系是否改变?若不改变，请求出此数量关系；若改变，请说明理由；
（3）当 ∠AEC=∠ACF 时，求 ∠APC 的度数．

24. 如图所示，在边长为 a 米的正方形草坪上修建两条宽为 b 米的道路．
（1）为了求得剩余草坪的面积，小明同学想出了两种办法，结果分别如下：
方法①： ；
方法②： ．
请你从小明的两种求面积的方法中，直接写出含有字母 a，b 代数式的等式是： ．
（2）根据（1）中的等式，解决如下问题：
①已知：a−b=5，a2+b2=20，求 ab 的值；
②已知：x−20182+x−20202=12，求 x−20192 的值．

25. 如图，在长方形 ABCD 中，AB=8 cm，BC=12 cm，点 E 为 AB 中点，如果点 P 在线段 BC 上以每秒 4 cm 的速度，由点 B 向点 C 运动，同时，点 Q 在线段 CD 上以 v 厘米/秒的速度，由点 C 向点 D 运动，设运动时间为 t 秒．
（1）直接写出：PC= 厘米，CQ= 厘米；（用含 t，v 的代数式表示）
（2）若以 E，B，P 为顶点的三角形和以 P，C，Q 为顶点的三角形全等，试求 v，t 的值；
（3）若点 Q 以（2）中的运动速度从点 C 出发，点 P 以原来的运动速度从点 B 同时出发，都逆时针方向沿长方形 ABCD 的四边运动，求经过多长时间点 P 与点 Q 第一次在长方形 ABCD 的哪条边上相遇?
答案
第一部分
1. C【解析】A选项：根据幂的乘方法则，底数不变，指数相乘，a23=a2×3=a6，本选项错误；
B选项：根据同底数幂的乘法法则，底数不变，指数相加，a2⋅a3=a2+3=a5，本选项错误；
C选项：根据同底数幂的乘法法则，底数不变，指数相加，2a⋅3a=6a2，本选项正确；
D选项：根据整式加减，系数相加，字母和指数不变，2a+3a=5a，本选项错误；
故选：C．
2. C【解析】∵∠BEF 是 △AEF 的外角，∠1=20∘，∠F=30∘，
∴∠BEF=∠1+∠F=50∘，
∵AB∥CD，
∴∠2=∠BEF=50∘，故选C．
3. B【解析】当 ∠1=∠A 时，可知是 DE 和 AC 被 AB 所截得到的同位角，可得到 DE∥AC，故A可以；
当 ∠A=∠3 时，可知是 AB，DF 被 AC 所截得到的同位角，可得 AB∥DF，故B不可以；
当 ∠3=∠4 时，可知是 DE 和 AC 被 AB 所截得到的内错角，可得 DE∥AC，故C可以；
当 ∠2+∠A=180∘ 时，一对同旁内角，可得 DE∥AC；故D可以；
故选：B．
4. A【解析】三角形底边 AC 上的高，为对角点 B 到边 AC 的垂线段．
∵BF⊥AC 于 F，
∴BF 是边 AC 上的高．
5. A
【解析】根据题意得，a，b 的值只要满足 a+b=−7,ab=12 即可，
A．−3+−4=−7，−3×−4=12，符合题意；
B .−3+4=1，−3×4=−12，不符合题意；
C．3+−4=−1，3×−4=−12，不符合题意；
D．3+4=7，3×4=12，不符合题意．
6. B【解析】带 2 去可以利用“角边角”能配一块与原来大小一样的三角形玻璃．
7. A【解析】根据题意可得：y=n100m+0.6．
8. C【解析】∵AB∥DE，
∴∠B=∠DEF，
可添加条件 BC=EF，
理由：
∵ 在 △ABC 和 △DEF 中，
AB=DE,∠B=∠DEF,BC=EF,
∴△ABC≌△DEFSAS．
9. D【解析】依据①②③④四部分的面积可得，b+c2=b2+2bc+c2，故A能验证；
依据⑤⑥两部分的面积可得，ab+c=ab+ac，故B能验证；
依据整个图形的面积可得，a+b+c2=a2+b2+c2+2ab+2bc+2ac，故C能验证；
图中不存在长为 a+2b，宽为 a 的长方形，故D选项不能验证；
故选：D．
10. B
【解析】本题考察实际问题与一次函数的图象．当点 P 从点 A 向点 D 移动时 S 逐渐增加；当点 P 在 DE 上移动时 S 不变；当点 P 在 EF 上移动时 S 逐渐减小；当点 P 在 FG 上移动时 S 不变；当点 P 在 GB 上移动时 S 逐渐减小，符合此特征的函数图象为B．
第二部分
11. 4x3y
【解析】原式=4x4y2÷xy=4x3y.
12. ∠FAD=∠EDA（或 AF∥DE）
【解析】条件 1：AF∥DE；
理由：
∵AB∥CD，
∴∠BAD=∠CDA，
∵AF∥DE，
∴∠FAD=∠EDA，
∴∠BAD−∠FAD=∠CDA−∠EDA，即 ∠1=∠2；
条件 2：∠FAD=∠EDA．
理由：
∵AB∥CD，
∴∠BAD=∠ADC，
∵∠FAD=∠EDA，
∴∠1=12∠BAD，∠2=12∠CDA，
∴∠1=∠2．
∴ 需要添加条件 ∠FAD=∠EDA 或者 AF∥DE．
13. 80
【解析】∵∠A+∠B+∠C=180∘，
又 ∵∠A=60∘，∠B=2∠C，
∵60∘+2∠C+∠C=180∘，
∴∠C=40∘，
∴∠B=80∘．
14. 136
【解析】从表中可以看出，烤鸭的质量每增加 0.5 千克，烤制的时间增加 20 分钟，由此可知烤制时间是烤鸭质量的一次函数．
设烤制时间为 t 分钟，烤鸭的质量为 x 千克，t 与 x 的一次函数关系式为：t=kx+b，
∴k+b=60,2k+b=100,
解得：k=40,b=20,
所以 t=40x+20．
当 x=2.9 千克时，t=40×2.9+20=136．
15. 3 秒
【解析】∵∠CMD=90∘，
∴∠CMA+∠DMB=90∘，
又 ∵∠CAM=90∘，
∴∠CMA+∠C=90∘，
∴∠C=∠DMB．
在 Rt△ACM 和 Rt△BMD 中，
∴∠A=∠B,∠C=∠DMB,CM=MD,
∴Rt△ACM≌Rt△BMDAAS，
∴AC=BM=3 m，
∵ 该人的运动速度为 1 m/s，
∴ 他到达点 M 时，运动时间为 3÷1=3s．
16. 173
【解析】∵a+b=20，ab=18，
∴S=a2+b2−12a2−12ba+b=12a2+b2−ab=12a+b2−3ab=12×202−3×18=173.
第三部分
17. 原式=−1+9−1=7.
18. 原式=4x2−y2−4x2−3xy+y2=−3xy.
当 x=13，y=−2 时，原式=2．
19. 如图所示，△ABC 即为所求．
20. （1） ∵∠A=∠ADE，
∴DE∥AC，
∴∠C+∠CDE=180∘；
∵∠CDE=3∠C，
∴∠C=45∘．
（2） ∵DE∥BC，
∴∠E=∠ABC，
∵∠C=∠E，
∴∠ABE=∠C，
∴BE∥CD．
21. （1） ∵AB=AD，AC=AE，BC=DE，
∴△ABC≌△ADESSS．
（2） 由 △ABC≌△ADE，则 ∠D=∠B，∠DAE=∠BAC．
∴∠DAE−∠ABE=∠BAC−∠BAE，即 ∠DAB=∠EAC．
设 AB 和 DE 交于点 O，
∵∠DOA=BOE，∠D=∠B，
∴∠DEB=∠DAB．
∴∠EAC=∠DEB．
22. （1） 4；5；5；16
【解析】①根据函数图象可知：AD=4，CD=5，BC=5．
②当点 P 运动到 CD 上时，△ABP 的面积达到最大值，
∴x=8 时，△ABP 的面积为 16．
（2） 当点 P 运动到点 D 时，有 △ABP 的面积为 16，
∴12×AB×AD=16，
∴AB=8，
∴ 四边形 ABCD 的面积为：12×5+8×4=26．
23. （1） ∵AB∥CD，
∴∠A+∠ACD=180∘，
∴∠ACD=180∘−40∘=140∘，
∵CE 平分 ∠ACP，CF 平分 ∠DCP，
∴∠ACP=2∠ECP，∠DCP=2∠PCF，
∴∠ECF=12∠ACD=70∘．
（2） 不变．数量关系为：∠APC=2∠AFC．
∵AB∥CD，
∴∠AFC=∠DCF，∠APC=∠DCP，
∵CF 平分 ∠DCP，
∴∠DCP=2∠DCF，
∴∠APC=2∠AFC．
（3） ∵AB∥CD，
∴∠AEC=∠ECD，
当 ∠AEC=∠ACF 时，则有 ∠ECD=∠ACF，
∴∠ACE=∠DCF，
∴∠PCD=12∠ACD=70∘，
∴∠APC=∠PCD=70∘．
24. （1） a−b2；a2−2ab+b2；a−b2=a2−2ab+b2
【解析】方法①：草坪的面积 =a−ba−b=a−b2．
方法②：草坪的面积 =a2−2ab+b2；
等式为：a−b2=a2−2ab+b2．
（2） ①把 a−b=5，a2+b2=20 代入 a−b2=a2−2ab+b2，
∴52=20−2ab，
∴ab=−2.5．
②原式可化为：x−2019+12+x−2019−12=12，
∴x−20192+2x−2019+1+x−20192−2x−2019+1=12，
∴2x−20192=10，
∴x−20192=5．
25. （1） 12−4t；vt．
【解析】根据题意得：PC=BC−BP=12−4t，CQ=vt．
（2） ∵ 点 E 是 AB 中点，
∴BE=4，
当 BP=CQ 时，BE=PC=4，△BEP≌△CQP，
∴4t=vt,4=12−4t,
解得：v=4,t=2,
当 BP=PC 时，BE=CQ=4，△BEP≌△CQP，
∴4t=6,4=vt,
解得：t=1.5,v=83.
（3） 根据题意可知，当 P，Q 两点的速度一样，都是 v=4 时，点 P 点与 Q 点永远不会相遇，故 v=4，不符合题意，舍去；
当点 P 速度为 4，点 Q 速度为 83 时，点 P 会与点 Q 相遇，
此时会有：4t=83t+12，
解得：t=9，
路程：4×9=36 cm，
∵BC=AD=12，CD=AB=8，
∴BC+CD+AD=42 cm，
∴ 走过 36 cm，点 P，Q 第一次相遇在 AD 上．