2018-2019学年广东省东莞市东城区东华初级中学七下期中数学试卷

这是一份2018-2019学年广东省东莞市东城区东华初级中学七下期中数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 在平面直角坐标系中，点 −2,5 所在的象限是
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

2. 在 −2，0.3030030003，227，−π，5 中为无理数有 个．
A. 4B. 3C. 2D. 1

3. 方程组 x+y=1,2x−y=5 解是
A. x=2,y=−1B. x=−2,y=3C. x=2,y=1D. x=−1,y=2

4. 下列命题是真命题的是
A. 若两个数的平方相等，则这两个数相等
B. 同位角相等
C. 同一平面内，垂直于同一直线的两条直线平行
D. 相等的角是对顶角

5. 下列计算正确的是
A. −2a2=2a2B. a6÷a3=a2
C. −2a−1=2−2aD. a⋅a2=a2

6. 如图，下列能判定 AB∥CD 的条件的个数是
（1）∠B+∠BCD=180∘；
（2）∠1=∠2；
（3）∠3=∠4；
（4）∠B=∠5．
A. 1 个B. 2 个C. 3 个D. 4 个

7. 在平面直角坐标系中，已知点 A−4,−1 和 B−1,4，平移线段 AB 得到线段 A1B1，使平移后点 A1 的坐标为 2,2，则平移后点 B1 坐标是
A. −3,1B. −3,7C. 1,1D. 5,7

8. 二元一次方程 2x+y=5 的正整数解有
A. 一组B. 2 组C. 3 组D. 无数组

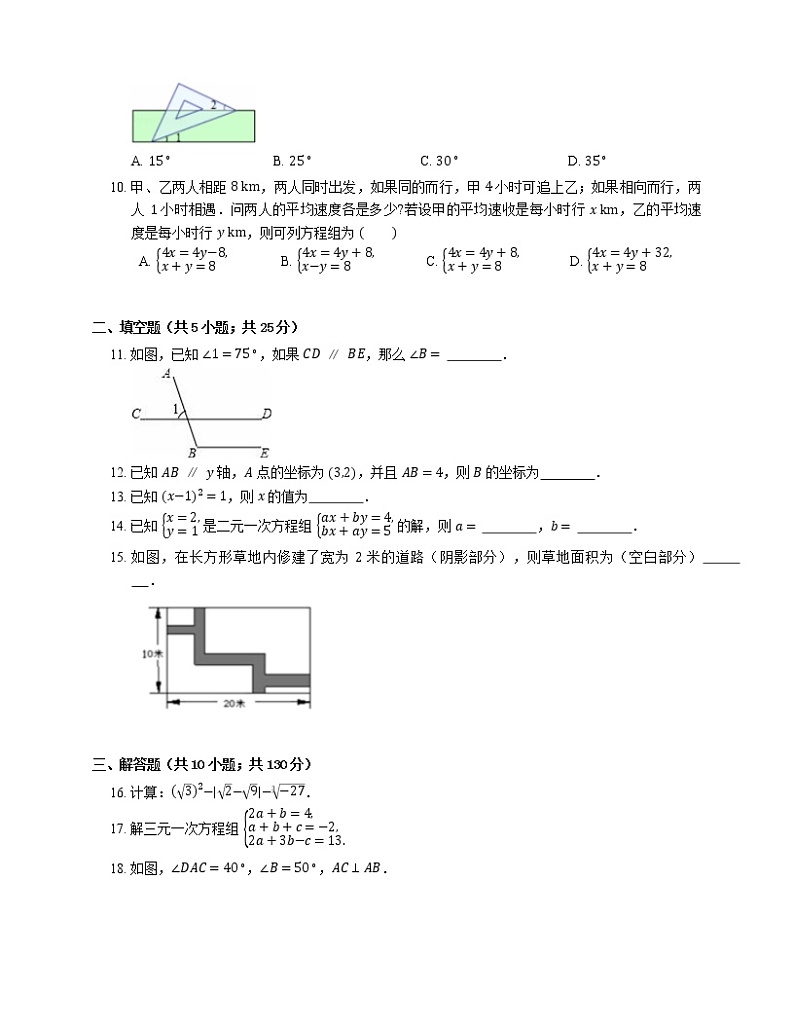
9. 如图，把一块含有 45∘ 角的直角三角板的两个顶点放在直尺的对边上．如果 ∠1=15∘，那么 ∠2 的度数是
A. 15∘B. 25∘C. 30∘D. 35∘

10. 甲、乙两人相距 8 km，两人同时出发，如果同的而行，甲 4 小时可追上乙；如果相向而行，两人 1 小时相遇．问两人的平均速度各是多少?若设甲的平均速收是每小时行 x km，乙的平均速度是每小时行 y km，则可列方程组为
A. 4x=4y−8,x+y=8B. 4x=4y+8,x−y=8C. 4x=4y+8,x+y=8D. 4x=4y+32,x+y=8

二、填空题（共5小题；共25分）
11. 如图，已知 ∠1=75∘，如果 CD∥BE，那么 ∠B= ．

12. 已知 AB∥y 轴，A 点的坐标为 3,2，并且 AB=4，则 B 的坐标为 ．

13. 已知 x−12=1，则 x 的值为 ．

14. 已知 x=2,y=1 是二元一次方程组 ax+by=4,bx+ay=5 的解，则 a= ，b= ．

15. 如图，在长方形草地内修建了宽为 2 米的道路（阴影部分），则草地面积为（空白部分） ．

三、解答题（共10小题；共130分）
16. 计算：32−2−9−3−27．

17. 解三元一次方程组 2a+b=4,a+b+c=−2,2a+3b−c=13.

18. 如图，∠DAC=40∘，∠B=50∘，AC⊥AB．
（1）求 ∠D+∠DCB 的度数；
（2）AB CD（直接填写平行或不一定平行，不必证明）．

19. 已知点 P 的坐标为 2−a,3a+6．
（1）若点 P 在 y 轴上，求点 P 坐标．
（2）若点 P 到两坐标轴的距离相等，求点 P 的坐标．

20. 已知 2a−3 的平方根是 ±5，2a+b+4 的立方根是 3，求 a+b 的平方根．

21. 在 y=kx+b 中，当 x=1 时，y=4，当 x=2 时，y=10．
（1）求 k 和 b 的值．
（2）求当 x=−2 时 y 的值．

22. 如图，在平面直角坐标系中，点 A4,0，B3,4，C0,2．
（1）求 S四边形ABCD（求四边形 ABCO 的面积）；
（2）在 x 轴上是否存在一点 P，使 S△APB=4（三角形 APB 的面积）?若存在，请直接写出点 P 坐标．

23. 如图，已知 CD⊥AB，GF⊥AB，∠B=∠ADE，试说明 ∠1=∠2．

24. 从甲地到乙地有一段下坡路与一段平路，如果保持下坡路每小时走 5 千米，平路每小时走 4 千米，上坡路每小时走 3 千米，那么从甲地到乙地需要 36 分钟，从乙地返回甲地需要 48 分钟．求甲地到乙地的全程是多少?

25. 如图，在直角坐标系系 xOy 中，已知 A36,0，B46,6，将线段 OA 平移至 CB，点 D 在 x 轴正半轴上（不与点 A 重合），连接 OC，AB，CD，BD．
（1）直接写出点 C 的坐标；
（2）当 △ODC 的面积是 △ABD 的面积的 2 倍时，求点 D 的坐标；
（3）若 ∠OCD=25∘，∠DBA=15∘，求 ∠BDC．并说明理由．
答案
第一部分
1. B【解析】∵ 第二象限内的点横坐标 <0，纵坐标 >0，
∴ 点 −2,5 所在的象限是第二象限．
2. C【解析】−2 是有理数，0.3030030003 是有理数，227 是有理数，−π 是无理数，5 是无理数，所以无理数有 2 个．
3. A【解析】x+y=1, ⋯⋯①2x−y=5, ⋯⋯②
①+② 得：3x=6，
解得：x=2，
把 x=2 代入 ①，得 2+y=1，
解得：y=−1，
所以方程组的解为：x=2,y=−1.
4. C【解析】A．若两个数的平方相等，则这两个数不一定相等，如 22=−22，但 2≠−2，故A选项错误；
B．只有两直线平行的情况下，才有同位角相等，故B选项错误；
C．同一平面内，垂直于同一直线的两条直线平行，真命题，符合题意；
D．相等的角不一定是对顶角，如图，∠1=∠2，但这两个角不符合对顶角的概念，故D选项错误，故选C．
5. C
【解析】A．−2a2=−22a2=4a2，选项错误；
B．a6÷a3=a6−3=a3，选项错误；
C．−2a−1=−2a+2=2−2a，选项正确；
D．a⋅a2=a1+2=a3，选项错误．
6. C【解析】当 ∠B+∠BCD=180∘，AB∥CD；
当 ∠1=∠2 时，AD∥BC；
当 ∠3=∠4 时，AB∥CD；
当 ∠B=∠5 时，AB∥CD．
7. D【解析】平移线段 AB 得到线段 A1B1，由 A−4,−1 的对应点 Aʹ 的坐标为 2,2，
可知：各对应点之间的关系是横坐标加 6，纵坐标加 3，
∴ 点 B1 的横坐标为 −1+6=5，纵坐标为 4+3=7，
∴ 点 B1 的坐标为 5,7．
8. B【解析】当 x=1，则 2+y=5，解得 y=3，
当 x=2，则 4+y=5，解得 y=1，
当 x=3，则 6+y=5，解得 y=−1，
所以原二元一次方程的正整数解为 x=1,y=3, x=2,y=1.
9. C【解析】如图所示：
由题意可得：∠1=∠3=15∘，则 ∠2=45∘−∠3=30∘．
10. C
【解析】设甲的平均速度是每小时行 x km，乙的平均速度是每小时行 y km，
由题意，得 4x=4y+8,x+y=8.
第二部分
11. 105∘
【解析】如图，
∵∠1=75∘，
∴∠2=180∘−75∘=105∘，
∵CD∥BE，
∴∠B=∠2=105∘．
12. 3,6 或 3,−2
【解析】∵AB∥y 轴，点 A 坐标为 3,2，
∴ 点 B 的横坐标为 3，
∵AB=4，
∴ 点 B 在点 A 的上方时，点 B 的纵坐标为 2+4=6，
点 B 在点 A 的下方时，点 B 的纵坐标为 2−4=−2，
∴ 点 B 的坐标为 3,6 或 3,−2．
13. 2 或 0
【解析】x−12=1，
x−1=±1，
x−1=1 或 x−1=−1，
解得：x=2 或 x=0．
14. 1，2
【解析】将 x=2,y=1 代入方程组 ax+by=4,bx+ay=5 得，
2a+b=4, ⋯⋯①2b+a=5, ⋯⋯②
①×2−② 得：3a=3，
解得：a=1，
把 a=1 代入 ① 得：2+b=4，
解得：b=2．
故答案为：1，2．
15. 144 米2
【解析】将道路分别向左、向上平移，得到草地为一个长方形，长方形的长为 20−2=18（米），宽为 10−2=8（米），则草地面积为 18×8=144 米2．
第三部分
16. 原式=3−3−2−−3=3−3+2+3=3+2.
17.
2a+b=4, ⋯⋯①a+b+c=−2, ⋯⋯②2a+3b−c=13, ⋯⋯③②+③
得：
3a+4b=11, ⋯⋯④①
与 ④ 联立得：
2a+b=4, ⋯⋯①3a+4b=11, ⋯⋯④①×4−④
得：
5a=5.
解得：
a=1.
把 a=1 代入 ① 得：
2+b=4.
解得：
b=2.
把 a=1，b=2 代入 ② 得：
1+2+c=−2.
解得：
c=−5.
所以方程组的解为：a=1,b=2,c=−5.
18. （1） ∵AC⊥AB，
∴∠BAC=90∘，
在 △ABC 中，∠BAC=90∘，∠B=50∘，
∴∠ACB=180∘−∠BAC−∠B=40∘，
∵∠DAC=40∘，
∴∠ACB=∠DAC，
∴AD∥BC，
∴∠D+∠DCB=180∘．
（2） 不一定平行
【解析】AB 与 CD 不一定平行，
∵ 已知条件中没有证明 AB 与 CD 平行的条件，
∴AB 与 CD 不一定平行．
19. （1） 由题意得：2−a=0，解得：a=2，
3a+6=12，
所以点 P 的坐标为 0,12．
（2） 根据题意得 ∣2−a∣=∣3a+6∣，
所以 2−a=3a+6 或 2−a=−3a+6，解得 a=−1 或 a=−4，
当 a=−1 时，2−a=3，3a+6=3，
所以点 P 坐标为 3,3；
当 a=−4 时，2−a=6，3a+6=−6，
所以点 P 坐标为 6,−6，
综上点 P 的坐标为 3,3 或 6,−6．
20. ∵2a−3 的平方根是 ±5，
∴2a−3=25，
∴a=14；
∵2a+b+4 立方根是 3，
∴2a+b+4=27，
∴b=−5；
∴a+b=14−5=9，
∴a+b 的平方根是 ±9=±3．
21. （1） 因为在 y=kx+b 中，当 x=1 时，y=4，当 x=2 时，y=10，
所以 4=k+b, ⋯⋯①10=2k+b, ⋯⋯②
②−① 得：k=6，
把 k=6 代入 ① 得：6+b=4，
解得：b=−2，
所以方程组的解为 k=6,b=−2,
所以 k=6，b=2．
（2） 由（1）知 y=6x−2，
当 x=−2 时，y=6×−2−2=−14．
22. （1） 如图，过点 B 作 BD⊥OA 于点 D．
∵A4,0，B3,4，C0,2，
∴OC=2，OD=3，BD=4，AD=4−3=1，
∴S四边形ABCO=S梯形CODB+S△ABD=12×2+4×3+12×1×4=9+2=11.
（2） 点 P 的坐标为 6,0 或 2,0．
【解析】存在，设点 Px,0，则 PA=x−4．
∵S△PAB=4，
∴12×x−4×4=4，
∴x−4=2，解得：x=6 或 x=2，
∴ 点 P 的坐标为 6,0 或 2,0．
23. ∵∠B=∠ADE（已知），
∴DE∥BC，（同位角相等，两直线平行）
∴∠1=∠DCB．（两直线平行，内错角相等）
∵CD⊥AB，GF⊥AB，
∴CD∥FG，（平面内，垂直于同一条直线的两条直线平行）
∴∠2=∠DCB．（两直线平行，同位角相等）
∴∠1=∠2．（等量代换）
24. 设从甲地到乙地的下坡路为 x km，平路为 y km，
由题意得：
x5+y4=3660,x3+y4=4860,
解得：
x=1.5,y=1.2.
所以：x+y=2.7 千米，
答：甲地到乙地的全程是 2.7 千米．
25. （1） C6,6
【解析】如图 1，延长 BC 交 y 轴于点 E，

∵A36,0，将线段 OA 平移至 CB，
∴BC=OA=36，
又 ∵B46,6，
∴BE=46，OE=6，
∴EC=BE−BC=46−36=6，
∴C6,6．
（2） 设 Dx,0，当 △ODC 的面积是 △ABD 的面积的 2 倍时，则有 OD=2AD，
若点 D 在线段 OA 上时，OD=x，AD=36−x，
∵OD=2AD，
∴12×6x=2×12×636−x，
∴x=26，
∴D26,0；
若点 D 在线段 OA 延长线上，OD=x，AD=x−36，
∵OD=2AD，
∴12×6x=2×12×6x−36，
∴x=66，
∴D66,0，
综上，点 D 坐标为 26,0 或 66,0．
（3） 如图 2，
过点 D 作 DF∥OC，
由平移的性质知 OC∥AB，
∴OC∥AB∥DF，
∴∠CDF=∠OCD=25∘，∠FDB=∠DBA=15∘，
∴∠CDB=∠CDF+∠FDB=25∘+15∘=40∘．