2021学年5.2 数学探究活动:由编号样本估计总数及其模拟课时练习

期末模拟试卷

B能力卷

一、   单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求.

1．已知集合，，则（    ）

A． B． C． D．

【答案】C

【详解】

解：，

，

解得：，

，

，

，

即.

2．设命题：，都有成立，则为（    ）

A．，都有成立 B．，有成立

C．，有成立 D．，有成立

【答案】B

【详解】

由原命题为全称命题，其否定为，否定结论，即“，有成立”，

故选：B

3．已知平面向量，且，则的值为（    ）

A．1 B． C．4 D．

【答案】D

【详解】

因为，

所以，解得：，

4．设，，，则的大小关系是（    ）

A． B． C． D．

【答案】D

【详解】

因为指数函数是减函数，所以，即；

又因为幂函数是增函数，所以，即，

所以.

5．函数的图象的大致形状是（    ）

A． B．

C． D．

【答案】D

【详解】

因为在上递减，在上递增， 所以只有选项正确.

6．“二十四节气”是上古农耕文明的产物，表达了人与自然宇宙之间独特的时间观念，是中华民族悠久文化内涵和历史沉淀.根据多年气象统计资料，某地在节气夏至当日下雨的概率为0.45，阴天的概率为0.20，则该地在节气夏至当日为晴天的概率为（    ）

A．0.65 B．0.55 C．0.35 D．0.75

【答案】C

【详解】

解：设事件“某地在节气夏至当日下雨”为事件A，"某地在节气夏至当日阴天”为事件B，“某地在节气夏至当日晴天”为事件C，

由题意可得事件A，B，C为互斥事件，所以，

又，所以.

7．已知函数，若关于的方程有4个不同的实数根，且所有实数根之和为2，则实数的取值范围是（    ）

A． B． C． D．

【答案】C

【详解】

设，

因为，

所以的图象关于直线对称，

设的4个不同的实数根为，

则，

则，

由题意可知，解得，

，

，的最小值为，

作出的大致图象，如图所示：

由图象可知，若关于的方程有4个不同的实数根，

则.

8．已知，，，当时，均有，则实数的取值范围是（    ）

A． B．

C． D．

【答案】B

【详解】

当时，均有，

即在上恒成立，

令，

由图像知：若时，，

即，

此时；

当时，，

即，

此时；

综上：或.

二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求. 全部选对的得5分，部分选对的得3分，有选错的得0分.

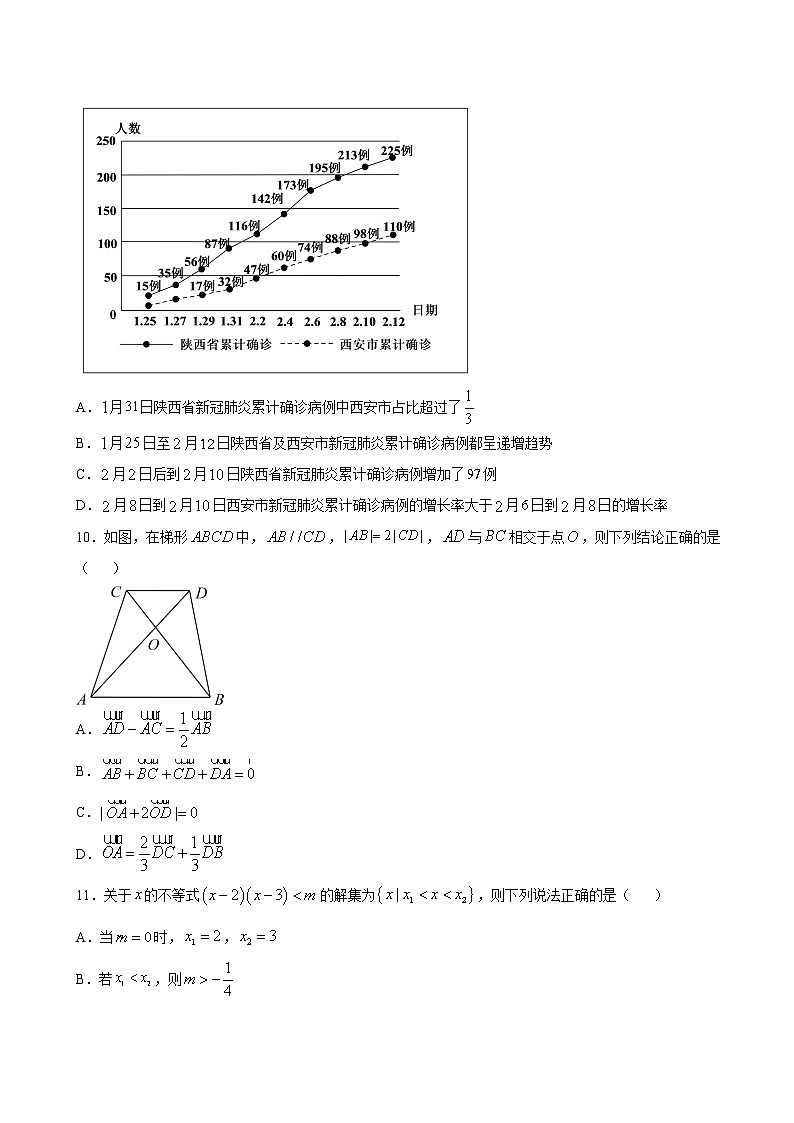
9．如图所示的曲线图是年月日至年月日陕西省及西安市新冠肺炎累计确诊病例的曲线图，则下列判断正确的是（    ）

A．月日陕西省新冠肺炎累计确诊病例中西安市占比超过了

B．月日至月日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势

C．月日后到月日陕西省新冠肺炎累计确诊病例增加了例

D．月日到月日西安市新冠肺炎累计确诊病例的增长率大于月日到月日的增长率

【答案】ABC

【详解】

对于A，月日陕西省新冠肺炎累计确诊病例中西安市占比为，故A正确，

对于B，月25日至月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势，故B正确，

对于C：月日后到月日陕西省新冠肺炎累计确诊病例增加了例，故C正确，

对于D：月日到月日西安市新冠肺炎累计确诊病例的增长率小于月日到月日的增长率，故D错误，

10．如图，在梯形中，，，与相交于点，则下列结论正确的是（    ）

A．

B．

C．

D．

【答案】ABC

【详解】

A.，所以A正确；

B. 正确，所以B正确；

C.，所以，即，所以，所以C正确；

D.，故D不正确.

11．关于的不等式的解集为，则下列说法正确的是（    ）

A．当时，，

B．若，则

C．当时，则

D．的零点是和

【答案】ABD

【详解】

A选项，当时，原不等式可化为，解得，所以，；A正确；

B选项，设，所以；

因为不等式的解集为，，即不等式有解，所以必有，B正确；

C选项，令，当时，可由函数向上平移个单位得到；又的零点为和；函数的零点为和；所以；C错；

D选项，由C选项可知，，

所以，令可得或，即的零点是和.故D正确.

12．已知函数，关于的不等式的解集为，则（    ）

A．

B．设，则的最小值一定为

C．不等式的解集为

D．若，且，则x的取值范围是

【答案】ACD

【详解】

由题意，即，∴，A正确；

，但当时，，B错；

，由已知，即，且，C正确；

由题意知在上是增函数，在上是常函数，因此由得或，解得或，综上，．D正确．

三、填空题：本题共4小题，每小题5分，共20分

13．已知幂函数过点，若，则实数的取值范围是________.

【答案】

【详解】

因为幂函数过点，

所以 ，

解得，

所以在 上递增，

又，

所以，即，

解得 ，

所以实数的取值范围是

14．已知，是两个不共线的向量，若向量与共线，则实数__________．

【答案】

【详解】

因为与共线，设，

又因为不共线，所以，所以，

15．甲、乙两队进行篮球决赛，采取三场二胜制（当一队赢得二场胜利时，该队获胜，决赛结束）．根据前期比赛成绩，甲队的主客场安排依次为“主客主”．设甲队主场取胜的概率为，客场取胜的概率为，且各场比赛结果相互独立，则甲队以获胜的概率是_____．

【答案】

【详解】

甲队的主客场安排依次为“主客主”．

设甲队主场取胜的概率为，客场取胜的概率为，且各场比赛结果相互独立，

甲队以获胜的是指甲队前两场比赛中一胜一负，第三场比赛甲胜，

则甲队以获胜的概率是：.

16．若区间满足：①函数在上有定义且单调；②函数在上的值域也为，则称区间为函数的共鸣区间．请完成：（1）写出函数的一个共鸣区间_______；（2）若函数存在共鸣区间，则实数k的取值范围是________．

【答案】或或       

【详解】

（1）设是区间上的共鸣区间，因为在上递增，且在上的值域也为，

所以，即，因为，所以或或，

函数的共鸣区间为或或.

（2）因为函数在上单调递增，若存在共鸣区间，则，即，也就是方程在上有两个不等的实根，

令，得，

所以在上有两个不等的实根，

令，

则，即，解得，

故实数k的取值范围是

四、解答题：本小题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤.

17．已知集合，函数的定义域为B．

（1）求，；

（2）已知集合，若，求实数m的取值范围．

【详解】

（1）由题意得，，所以集合，

对于函数，，解得集合，

所以，，

所以；

（2）由（1）得，因为，

当时，，解得，满足题意；

当时，或，

解得或，

综上，实数m的取值范围为或.

18．在①，②，③对任意实数x，y，均有这三个条件中任选一个，补充在下面问题中并解答.已知函数满足_________，求的解析式.注：如果选择多个条件解答，按第一个解答计分.

【详解】

选①，令，则.

因为，

所以

即.

选②，因为，（1）

所以.（2）

（2）（1）得，

即.

选③，令，则，即.

令，则，所以，

19．设（，），且.

（1）求实数a的值及函数的定义域；

（2）证明的奇偶性，并求函数在区间上的最小值.

【答案】（1）；定义域是；（2）证明见解析；最小值为0.

【详解】

（1）由题意，函数（，），

因为，可得，解得，

所以函数，则满足，解得，

所以函数的定义域是.

（2）由题意，函数的定义域为关于原点对称，

又由，即，所以为奇函数，

因为，，

设，可得函数在区间上单调递增，

根据复数函数的单调性，可得函数在区间上单调递增，

当时，在区间上取得最小值，是.

20．已知函数（为实数）.

（1）若，求的单调区间.

（2）若，设在区间的最小值为，求的解析式.

（3）设，，若，恒成立，求的取值范围.

【详解】

（1）当时，函数，.

如图所示：

由图知：的单调增区间是 ，单调减区间是：.

（2）因为，且，

如图所示：

当，即时，，

当，即时，，

当，即时，，

综上：.

（3）当时，，

因为，

所以，

所以在上增函数，

所以，

因为，恒成立，

，即，

解得，

所以的取值范围是.

21．“金山银山，不如绿水青山，而且绿水青山就是金山银山”.某乡镇为创建“绿色家园”，决定在乡镇范围内栽种某种观赏树木，已知这种树木自栽种之日起，其生长规律为：树木的高度（单位：米）与生长年限（单位：年）满足关系，树木栽种时的高度为米；1年后，树木的高度达到米.

（1）求的解析式；

（2）问从种植起，第几年树木生长最快？

【详解】

（1）由已知得，即，

所以，解得，，

所以，.

（2）令，.

问题化为，当时，求函数的最大值.

而

.

当且仅当，即，上式取等号，但，，

故种植之日起，第3年与第4年树木生长最快.

22．已知函数是定义域上的奇函数，且．

（1）求函数的解析式，判断函数在上的单调性并证明；

（2）令，若函数在上有两个零点，求实数的取值范围；

（3）令，若对，都有，求实数的取值范围．

【详解】

（1），且是奇函数，，

，解得，

．

函数在上单调递减，在上单调递增，

证明如下：任取，，且，

则，

，且，

，，

∴，

，即，

函数在上单调递减.

同理可证明函数在上单调递增．

（2）函数在上有两个零点，即方程在上有两个不相等的实数根，

所以在上有两个不相等的实数根，

则，解得．

（3）由题意知，

令，，

由（1）可知函数在上单调递减，在上单调递增，

，

函数的对称轴方程为，

函数在上单调递增，

当时，取得最小值，；

当时，取得最大值，.

所以，，

又对任意的，都有恒成立，

，

即，

解得，又，

的取值范围是．