2018年北京市平谷区中考一模数学试卷

这是一份2018年北京市平谷区中考一模数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 风和日丽春光好，又是一年舞筝时．放风筝是我国人民非常喜爱的一项户外娱乐活动．下列风筝剪纸作品中，不是轴对称图形的是
A. B.
C. D.

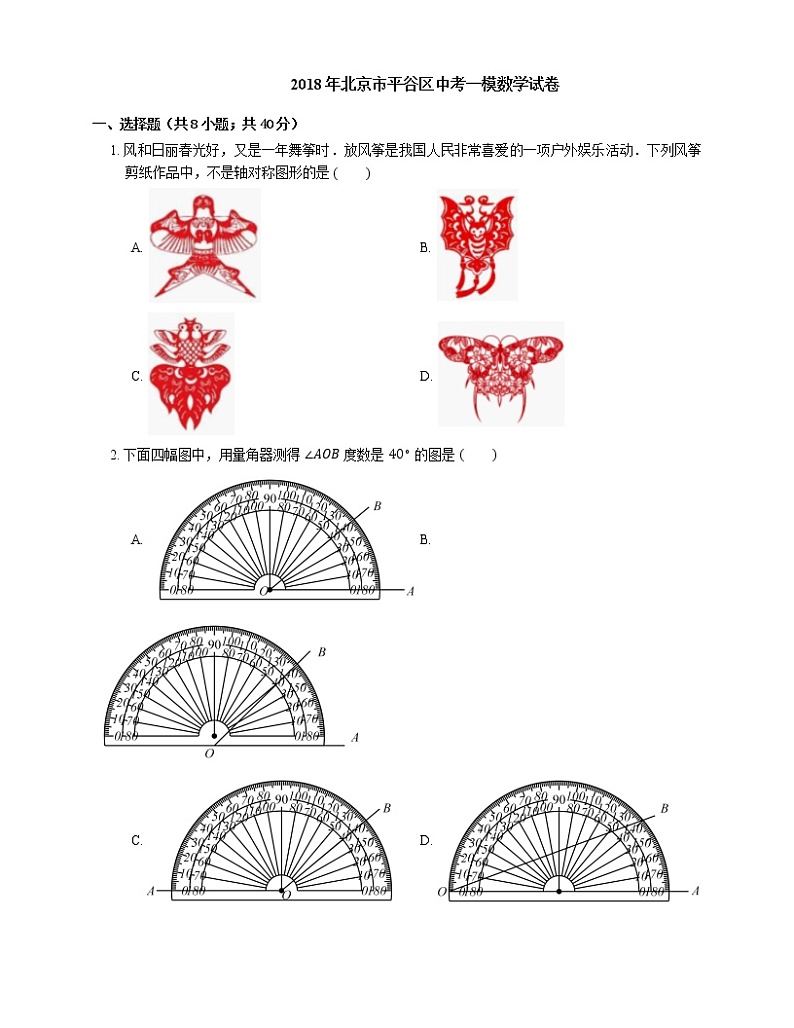
2. 下面四幅图中，用量角器测得 ∠AOB 度数是 40∘ 的图是
A. B.
C. D.

3. 如图，数轴上每相邻两点距离表示 1 个单位，点 A，B 互为相反数，则点 C 表示的数可能是
A. 0B. 1C. 3D. 5

4. 如图可以折叠成的几何体是
A. 三棱柱B. 圆柱C. 四棱柱D. 圆锥

5. 中国有个名句“运筹帷幄之中，决胜千里之外”．其中的“筹”原意是指《孙子算经》中记载的“算筹”．算筹是古代用来进行计算的工具，它是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图）．当表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间：个位、百位、万位数用纵式表示；十位，千位，十万位数用横式表示；“0”用空位来代替，以此类推．例如 3306 用算筹表示就是，则 2022 用算筹可表示为
A. B.
C. D.

6. 一个正多边形的每个内角的度数都等于相邻外角的度数，则该正多边形的边数是
A. 3B. 4C. 6D. 12

7. “龟兔赛跑”是同学们熟悉的寓言故事．如图所示，表示了寓言中的龟、兔的路程 S 和时间 t 的关系（其中直线段表示乌龟，折线段表示兔子）．下列叙述正确的是
A. 赛跑中，兔子共休息了 50 分钟
B. 乌龟在这次比赛中的平均速度是 0.1 米/分钟
C. 兔子比乌龟早到达终点 10 分钟
D. 乌龟追上兔子用了 20 分钟

8. 中小学时期是学生身心变化最为明显的时期，这个时期孩子们的身高变化呈现一定的趋势，7∼15 岁期间生子们会经历一个身高发育较迅速的阶段，我们把这个年龄阶段叫做生长速度峰值段，小明通过上网查阅《 2016 年某市儿童体格发育调查表》，了解某市男女生 7∼15 岁身高平均值记录情况，并绘制了如下统计图，并得出以下结论：
① 10 岁之前，同龄的女生的平均身高一般会略高于男生的平均身高；
② 10∼12 岁之间，女生达到生长速度峰值段，身高可能超过同龄男生；
③ 7∼15 岁期间，男生的平均身高始终高于女生的平均身高；
④ 13∼15 岁男生身高出现生长速度峰值段，男女生身高差距可能逐渐加大．
以上结论正确的是
A. ①③B. ②③C. ②④D. ③④

二、填空题（共8小题；共40分）
9. 二次根式 x−2 有意义，则 x 的取值范围是 ．

10. 林业部门要考察某种幼树在一定条件下的移植成活率，如图是这种幼树在移植过程中幼树成活率的统计图，估计该种幼树在此条件下移植成活的概率为 （结果精确到 0.01）．

11. 计算：2+2+⋯+2m个2+3×3×⋯×3n个3= ．

12. 如图，测量小玻璃管口径的量具 ABC 上，AB 的长为 10 毫米，AC 被分为 60 等份，如果小管口中 DE 正好对着量具上 20 份处（DE∥AB），那么小管口径 DE 的长是 毫米．

13. 已知：a2+a=4，则代数式 a2a+1−a+2a−2 的值是 ．

14. 如图，AB 是 ⊙O 的直径，AB⊥弦CD 于点 E，若 AB=10，CD=8，则 BE= ．

15. 如图，在平面直角坐标系 xOy 中，△OCD 可以看作是 △ABO 经过若干次图形的变化（平移，轴对称，旋转）得到的，写出一种由 △ABO 得到 △OCD 的过程： ．

16. 下面是“作已知角的角平分线”的尺规作图过程．
已知：如图 1，∠MON．
求作：射线 OP，使它平分 ∠MON．
作法：如图 2，
（1）以点 O 为圆心，任意长为半径作弧，交 OM 于点 A，交 ON 于点 B；
（2）连接 AB；
（3）分别以点 A，B 为圆心，大于 12AB 的长为半径作弧，两弧相交于点 P；
（4）作射线 OP．
所以，射线 OP 即为所求作的射线．
请回答：该尺规作图的依据是 ．

三、解答题（共12小题；共156分）
17. 计算：13−1−π−30+∣1−3∣−2sin60∘．

18. 解不等式组 3x−1≥4x−5,x−1>x−53, 并写出它的所有整数解．

19. 如图，在 △ABC 中，AB=AC，点 D 是 BC 边上一点，EF 垂直平分 CD，交 AC 于点 E，交 BC 于点 F，连接 DE，求证：DE∥AB．

20. 关于 x 的一元二次方程 x2+2x+k−1=0 有两个不相等的实数根．
（1）求 k 的取值范围；
（2）当 k 为正整数时，求此时方程的根．

21. 如图，在平面直角坐标系 xOy 中，函数 y=kxk≠0 的图象与直线 y=x+1 交于点 A1,a．
（1）求 a，k 的值；
（2）连接 OA，点 P 是函数 y=kxk≠0 上一点，且满足 OP=OA，直接写出点 P 的坐标（点 A 除外）．

22. 如图，在平行四边形 ABCD 中，BF 平分 ∠ABC 交 AD 于点 F，AE⊥BF 于点 O，交 BC 于点 E，连接 EF．
（1）求证：四边形 ABEF 是菱形；
（2）连接 CF，若 ∠ABC=60∘，AB=4，AF=2DF，求 CF 的长．

23. 为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整．
收集数据
随机抽取甲乙两所学校的 20 名学生的数学成绩进行分析：
甲91897786713197937291 81928585958888904491乙84936669768777828588 90886788919668975988
（1）整理、描述数据
按如下数据段整理、描述这两组数据
（2）分析数据
两组数据的平均数、中位数、众数、方差如下表：
经统计，表格中 m 的值是 ．
（3）得出结论
a若甲学校有 400 名初二学生，估计这次考试成绩 80 分以上人数为 ．
b可以推断出 学校学生的数学水平较高，理由为 ．（至少从两个不同的角度说明推断的合理性）

24. 如图，以 AB 为直径作 ⊙O，过点 A 作 ⊙O 的切线 AC，连接 BC，交 ⊙O 于点 D，点 E 是 BC 边的中点，连接 AE．
（1）求证：∠AEB=2∠C；
（2）若 AB=6，csB=35，求 DE 的长．

25. 如图，在 △ABC 中，∠C=60∘，BC=3 厘米，AC=4 厘米，点 P 从点 B 出发，沿 B→C→A 以每秒 1 厘米的速度匀速运动到点 A．设点 P 的运动时间为 x 秒，B，P 两点间的距离为 y 厘米．小新根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究．下面是小新的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如表：
经测量 m 的值是 （保留一位小数）．
（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在 △ABC 中画出点 P 所在的位置．

26. 在平面直角坐标系 xOy 中，抛物线 y=−x2+2bx−3 的对称轴为直线 x=2．
（1）求 b 的值；
（2）在 y 轴上有一动点 P0,m，过点 P 作垂直 y 轴的直线交抛物线于点 Ax1,y1，Bx2,y2，其中 x1①当 x2−x1=3 时，结合函数图象，求出 m 的值；
②把直线 PB 下方的函数图象，沿直线 PB 向上翻折，图象的其余部分保持不变，得到一个新的图象 W，新图象 W 在 0≤x≤5 时，−4≤y≤4，求 m 的取值范围．

27. 在 △ABC 中，AB=AC，CD⊥BC 于点 C，交 ∠ABC 的平分线于点 D，AE 平分 ∠BAC 交 BD 于点 E，过点 E 作 EF∥BC 交 AC 于点 F，连接 DF．
（1）补全图 1；
（2）如图 1，当 ∠BAC=90∘ 时，
①求证：BE=DE；
②写出判断 DF 与 AB 的位置关系的思路（不用写出证明过程）；
（3）如图 2，当 ∠BAC=α 时，直接写出 α，DF，AE 的关系．

28. 在平面直角坐标系 xOy 中，点 M 的坐标为 x1,y1，点 N 的坐标为 x2,y2，且 x1≠x2，y1≠y2，以 MN 为边构造菱形，若该菱形的两条对角线分别平行于 x 轴，y 轴，则称该菱形为边的“坐标菱形”．
（1）已知点 A2,0，B0,23，则以 AB 为边的“坐标菱形”的最小内角为 ；
（2）若点 C1,2，点 D 在直线 y=5 上，以 CD 为边的“坐标菱形”为正方形，求直线 CD 表达式；
（3）⊙O 的半径为 2，点 P 的坐标为 3,m．若在 ⊙O 上存在一点 Q，使得以 QP 为边的“坐标菱形”为正方形，求 m 的取值范围．
答案
第一部分
1. B
2. A
3. C
4. A
5. C
6. B
7. D
8. C
第二部分
9. x≥2
10. 0.88
11. 2m+3n
12. 103
13. 8
14. 2
15. 答案不唯一，如：将 △ABO 沿 x 轴向下翻折，在沿 x 轴向左平移 2 个单位长度得到 △OCD
16. 答案不唯一：到线段两端点距离相等的点在线段的垂直平分线上；等腰三角形三线合一
第三部分
17. 13−1−π−30+∣1−3∣−2sin60∘=3−1+3−1−2×32=1.
18.
3x−1≥4x−5, ⋯⋯①x−1>x−53, ⋯⋯②
解不等式 ①，得
x≤2.
解不等式 ②，得
x>−1.
所以原不等式组的解集为
−1所以适合原不等式组的整数解为 0，1，2．
19. ∵AB=AC，
∴∠B=∠C．
∵EF 垂直平分 CD，
∴ED=EC．
∴∠EDC=∠C．
∴∠EDC=∠B．
∴DF∥AB．
20. （1） ∵ 关于 x 的一元二次方程有两个不相等的实数根．
∴Δ=22−4k−1>0=8−4k>0.
∴k<2．
（2） ∵k 为正整数，
∴k=1，
解方程 x2+2x=0，得 x1=0，x2=−2．
21. （1） ∵ 直线 y=x+1 经过点 A1,a，
∴a=2.
∴A1,2，
∵ 函数 y=kxk≠0 的图象经过点 A1,2，
∴k=2．
（2） 点 P 的坐标 2,1，−1,−2，−2,−1．
22. （1） ∵BF 平分 ∠ABC，
∴∠ABF=∠CBF，
∵ 平行四边形 ABCD，
∴AD∥BC，
∴∠AFB=∠CBF，
∴∠ABF=∠AFB，
∴AB=AF，
∵AE⊥BF，
∴∠ABF+∠BAO=∠CBF+∠BEO=90∘，
∴∠BAO=∠BEO，
∴AB=BE，
∴AF=BE，
∴ 四边形 ABEF 是平行四边形．
∴ 平行四边形 ABEF 是菱形．
（2） ∵AD=BC，AF=BE，
∴DF=CE，
∴BE=2CE，
∵AB=4，
∴BE=4，
∴CE=2，
过点 A 作 AG⊥BC 于点 G，
∵∠ABC=60∘，AB=BE，
∴△ABE 是等边三角形．
∴BG=GE=2，
∴AF=CG=4，
∴ 四边形 AGCF 是平行四边形．
∴ 平行四边形 AGCF 是矩形，
∴AG=CF，
在 △ABG 中，∠ABC=60∘，AB=4，
∴AG=23，
∴CF=23．
23. （1） 整理、描述数据
（2） 88
（3） 300；答案不唯一；理由须支撑推断结论
24. （1） ∵AC 是 ⊙O 的切线，
∴∠BAC=90∘．
∵ 点 E 是 BC 边的中点，
∴AE=EC．
∴∠C=∠EAC，
∵∠AEB=∠C+∠EAC，
∴∠AEB=2∠C．
（2） 连接 AD．
∵AB 为直径作 ⊙O，
∴∠ABD=90∘．
∵AB=6，csB=35，
∴BD=185．
在 Rt△ABC 中，AB=6，csB=35，
∴BC=10．
∵ 点 E 是 BC 边的中点，
∴BE=5．
∴DE=75．
25. （1） 3.0
（2） 如图所示；
（3） 如图．
26. （1） ∵ 抛物线 y=−x2+2bx−3 的对称轴为直线 x=2，
∴b=2．
（2） ① ∴ 抛物线的表达式为 y=−x2+4x−3．
∵Ax1,y，Bx2,y，
∴ 直线 AB 平行 x 轴．
∵x2−x1=3，
∴AB=3．
∵ 对称轴为 x=2，
∴AC=12．
∴ 当 x=12 时，y=m=−54．
②当 y=m=−4 时，0≤x≤5 时，−4≤y≤1；
当 y=m=−2 时，0≤x≤5 时，−2≤y≤4；
∴m 的取值范围为 −4≤m≤−2．
27. （1） 补全图 1；
（2） ①延长 AE，交 BC 于点 H．
∵AB=AC，AE 平分 ∠BAC，
∴AH⊥BC 于 H，BH=HC．
∵CD⊥BC 于点 C，
∴EH∥CD．
∴BE=DE．
②延长 FE，交 AB 于点 G．
由 AB=AC，得 ∠ABC=∠ACB．
由 EF∥BC，得 ∠AGF=∠AFG．
得 AG=AF．
由等腰三角形三线合一得 GE=EF
由 ∠GEB=∠FED，可证 △BEG≌△DEF．
可得 ∠ABE=∠FDE．
从而可证得 DF∥AB．
（3） DFAE=tanα2．
28. （1） 60
（2） ∵ 以 CD 为边的“坐标菱形”为正方形，
∴ 直线 CD 与直线 y=5 的夹角是 45∘．
过点 C 作 CE⊥DE 于 E．
∴D4,5或−2,5．
∴ 直线 CD 的表达式为 y=x+1 或 y=−x+3．
（3） 1≤m≤5 或 −5≤m≤−1．