2018年北京市延庆区中考一模数学试卷

这是一份2018年北京市延庆区中考一模数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
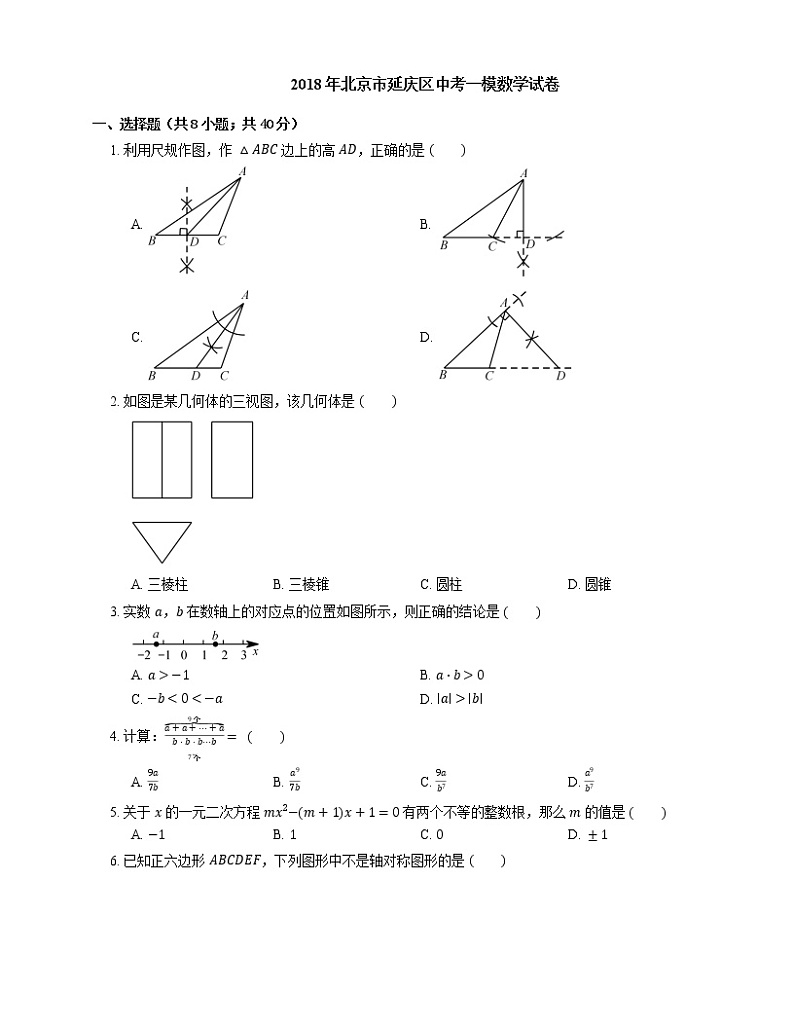
1. 利用尺规作图，作 △ABC 边上的高 AD，正确的是
A. B.
C. D.

2. 如图是某几何体的三视图，该几何体是
A. 三棱柱B. 三棱锥C. 圆柱D. 圆锥

3. 实数 a，b 在数轴上的对应点的位置如图所示，则正确的结论是
A. a>−1B. a⋅b>0
C. −b<0<−aD. a>b

4. 计算：a+a+⋯+a9个b⋅b⋅b⋯b⏟7个=
A. 9a7bB. a97bC. 9ab7D. a9b7

5. 关于 x 的一元二次方程 mx2−m+1x+1=0 有两个不等的整数根，那么 m 的值是
A. −1B. 1C. 0D. ±1

6. 已知正六边形 ABCDEF，下列图形中不是轴对称图形的是
A. B.
C. D.

7. 如图的统计图反映了我国 2013 年到 2017 年国内生产总值情况（以下数据摘自国家统计局《中华人民共和国 2017 年国民经济和社会发展统计公报》）．根据统计图提供的信息，下列推断不合理的是
A. 与 2016 年相比，2017 年我国国内生产总值有所增长
B. 2013∼2016 年，我国国内生产总值的增长率逐年降低
C. 2013∼2017 年，我国国内生产总值的平均增长率约为 6.7%
D. 2016∼2017 年比 2014∼2015 年我国国内生产总值增长的多

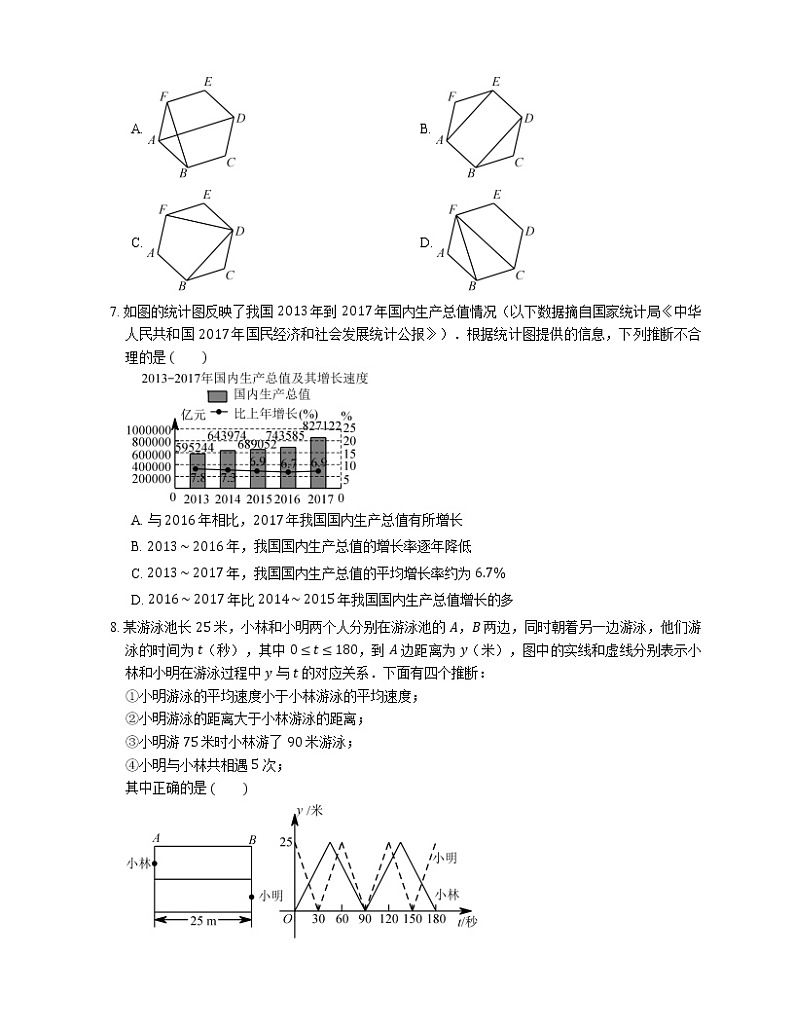
8. 某游泳池长 25 米，小林和小明两个人分别在游泳池的 A，B 两边，同时朝着另一边游泳，他们游泳的时间为 t（秒），其中 0≤t≤180，到 A 边距离为 y（米），图中的实线和虚线分别表示小林和小明在游泳过程中 y 与 t 的对应关系．下面有四个推断：
①小明游泳的平均速度小于小林游泳的平均速度；
②小明游泳的距离大于小林游泳的距离；
③小明游 75 米时小林游了 90 米游泳；
④小明与小林共相遇 5 次；
其中正确的是
A. ①②B. ①③C. ③④D. ②④

二、填空题（共8小题；共40分）
9. 若分式 x+2x−3 有意义，则实数 x 的取值范围是 ．

10. 如图是一个正五边形，则 ∠1 的度数是 ．

11. 如果 a2−a−1=0，那么代数式 a−2a−1a⋅a2a−1 的值是 ．

12. 如图，在 △ABC 中，D，E 分别是 AB，AC 上的点，DE∥BC，若 AD=1，BD=3，则 DEBC 的值为 ．

13. 2017 年延庆区农业用水和居民家庭用水的总和为 8 亿立方米，其中居民家庭用水比农业用水的 2 倍还多 0.5 亿立方米．设农业用水为 x 亿立方米，居民家庭用水为 y 亿立方米．依题意，可列方程组为 ．

14. 如图，AB 是 ⊙O 的弦，OC⊥AB，∠AOC=42∘，那么 ∠CDB 的度数为 ．

15. 如图，在平面直角坐标系 xOy 中，△DEF 可以看作是 △ABC 经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由 △ABC 得到 △DEF 的过程： ．

16. 某农科所在相同条件下做玉米种子发芽实验，结果如图．某位顾客购进这种玉米种子 10 千克，那么大约有 千克种子能发芽．

三、解答题（共12小题；共156分）
17. 计算：3tan30∘+∣1−3∣+2−π0−13−1．

18. 解不等式组：5x−2<3x+2,x+52≤3x. 并写出它的所有整数解．

19. 如图，在 △ABC 中，AD 平分 ∠BAC 交 BC 于点 D，过点 D 作 DE∥AB 交 AC 于点 E．求证：AE=DE．

20. 已知：∠AOB 及边 OB 上一点 C．
求作：∠OCD，使得 ∠OCD=∠AOB．
要求：
（1）尺规作图，保留作图痕迹，不写做法；（说明：作出一个即可）
（2）请你写出作图的依据．

21. 如图，Rt△ABC 中，∠ABC=90∘，点 D，F 分别是 AC，AB 的中点，CE∥DB，BE∥DC．
（1）求证：四边形 DBEC 是菱形；
（2）若 AD=3，DF=1，求四边形 DBEC 面积．

22. 在平面直角坐标系 xOy 中，直线 y=kx+bk≠0 与 x 轴交于点 A，与 y 轴交于点 B，与反比例函数 y=mxm≠0 的图象在第一象限交于点 P1,3，连接 OP．
（1）求反比例函数 y=mxm≠0 的表达式；
（2）若 △AOB 的面积是 △POB 的面积的 2 倍，求直线 y=kx+b 的表达式．

23. 如图，AB 是 ⊙O 的直径，D 是 ⊙O 上一点，点 E 是 AD 的中点，过点 A 作 ⊙O 的切线交 BD 的延长线于点 F．连接 AE 并延长交 BF 于点 C．
（1）求证：AB=BC；
（2）如果 AB=5，tan∠FAC=12，求 FC 的长．

24. 从北京市环保局证实，为满足 2022 年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．
过程如下，请补充完整．
收集数据：
从 2016 年 12 月初开始，连续一年对两镇的空气质量进行监测（将 30 天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12 个月的空气污染指数如下：
千家店镇:1201151001009585807050505045永宁镇11090105809085906090457060
（1）整理、描述数据：
按如表整理、描述这两镇空气污染指数的数据：
（说明：空气污染指数 ≤50 时，空气质量为优；50＜ 空气污染指数 ≤100 时，空气质量为良；100< 空气污染指数 ≤150 时，空气质量为轻微污染．）
分析数据：
两镇的空气污染指数的平均数、中位数、众数如表所示；
城镇平均数中位数众数千家店8050永宁81.387.5
请将以上两个表格补充完整；
得出结论：可以推断出 镇这一年中环境状况比较好，理由为 ．（至少从两个不同的角度说明推断的合理性）

25. 如图，点 P 是以 O 为圆心，AB 为直径的半圆上的动点，AB=6 cm，设弦 AP 的长为 x cm，△APO 的面积为 y cm2（当点 P 与点 A 或点 B 重合时，y 的值为 0）．小明根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；
（1）通过取点、画图、测量、计算，得到了 x 与 y 的几组值，如表：
那么 m= ；（保留一位小数）
（2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．
（3）结合函数图象说明，当 △APO 的面积是 4 时，则 AP 的值约为 ．（保留一位小数）

26. 在平面直角坐标系 xOy 中，抛物线 y=ax2−4ax+3aa>0 与 x 轴交于 A，B 两点（A 在 B 的左侧）．
（1）求抛物线的对称轴及点 A，B 的坐标；
（2）点 Ct,3 是抛物线 y=ax2−4ax+3aa>0 上一点（点 C 在对称轴的右侧），过点 C 作 x 轴的垂线，垂足为点 D．
①当 CD=AD 时，求此时抛物线的表达式；
②当 CD>AD 时，求 t 的取值范围．

27. 如图 1，正方形 ABCD 中，点 E 是 BC 延长线上一点，连接 DE，过点 B 作 BF⊥DE 于点 F，连接 FC．
（1）求证：∠FBC=∠CDF．
（2）作点 C 关于直线 DE 的对称点 G，连接 CG，FG．
①依据题意补全图形；
②用等式表示线段 DF，BF，CG 之间的数量关系并加以证明．

28. 平面直角坐标系 xOy 中，点 Ax1,y1 与 Bx2,y2，如果满足 x1+x2=0，y1−y2=0，其中 x1≠x2，则称点 A 与点 B 互为反等点．已知：点 C3,4．
（1）下列各点中， 与点 C 互为反等点；
D−3,−4，E3,4，F−3,4
（2）已知点 G−5,4，连接线段 CG，若在线段 CG 上存在两点 P，Q 互为反等点，求点 P 的横坐标 xP 的取值范围；
（3）已知 ⊙O 的半径为 r，若 ⊙O 与（2）中线段 CG 的两个交点互为反等点，求 r 的取值范围．
答案
第一部分
1. B
2. A
3. C
4. C
5. A
6. D
7. C
8. D
第二部分
9. x≠3
10. 72∘
11. 1
12. 1:4
13. x+y=8,y=2x+0.5
14. 21∘
15. △ABC 沿 y 轴翻折后，再向上平移 4 个单位得到 △DEF
16. 8.8
第三部分
17. 原式=3×33+3−1+1−3=23−3.
18. 由 ① 得，
x<4.
由 ② 得，
x≥1.∴
原不等式组的解集为
1≤x<4.∴
原不等式组的所有整数解为 1，2，3．
19. ∵AD 平分 ∠BAC，
∴∠BAD=∠DAE，
∵DE∥AB，
∴∠BAD=∠ADE，
∴∠DAE=∠ADE，
∴AE=DE．
20. （1） 作图（略）．
（2） 到线段两端点距离相等的点在线段的垂直平分线上；垂直平分线上的点到线段两端点距离相等；等边对等角．
21. （1） 在 Rt△ABC 中，
∵CE∥DC，BE∥DC，
∴ 四边形 DBEC 是平行四边形，
∵D 是 AC 的中点，∠ABC=90∘，
∴BD=DC，
∴ 四边形 DBEC 是菱形．
（2） ∵F 是 AB 的中点，
∴BC=2DF=2，∠AFD=∠ABC=90∘，
∴S菱形DBEC=2S△DBC=42，
在 Rt△AFD 中，AF=AD2−DF2=32−1=22，
∴S△DBC=12BC×BF=12×2×22=22．
22. （1） y=3x．
（2） 如图（1）：
∵S△AOB=2S△POB，
∴OA=2PE=2，
∴A2,0，
将 A2,0，P1,3 代入 y=kx+b，
可得 0=2k+b,3=k+b,
∴k=−3,b=6,
∴ 直线 AB 的表达式为：y=−3x+6，
同理：如图（2）直线 AB 的表达式为：y=x+2，
综上：直线 AB 的表达式为 y=−3x+6 或 y=x+2．
23. （1） 连接 BE．
∵AB 是直径，
∴∠AEB=90∘．
∴∠CBE+∠ECB=90∘，∠EBA+∠EAB=90∘．
∵ 点 E 是 AD 的中点，
∴∠CBE=∠EBA．
∴∠ECB=∠EAB．
∴AB=BC．
（2） ∵FA 作 ⊙O 的切线，
∴FA⊥AB．
∴∠FAC+∠EAB=90∘．
∵∠EBA+∠EAB=90∘，
∴∠FAC=∠EBA．
∵tan∠FAC=12AB=5，
∴AE=5，BE=25．
过 C 点作 CH⊥AF 于点 H，
∵AB=BC，∠AEB=90∘，
∴AC=2AE=25．
∵tan∠FAC=12，
∴CH=2．
∵CH∥AB，AB=BC=5，
∴25=FCFC+5．
∴FC=103．
24. 1；9；2
82.5；90
千家店镇；千家店镇污染指数平均数为 80，永宁镇污染指数平均数为 81.3，所以千家店镇污染指数平均数较低，空气质量较好；千家店镇空气质量为优的天数是 4 天，永宁镇空气质量为优的天数是 1 天，所以千家店镇空气质量为优的天数多，空气质量较好
25. （1） 约 4.3
（2）
（画此函数图象时要体现出 x 约为 4.2 时，y 有最大值，为 4.5）
（3） 3.1 或是 5.1
26. （1） 对称轴：x=2，A1,0 或 B3,0．
（2） ①如图，
∵AD=CD，
∴AD=3，
∴C 点坐标为 4,3，
将 C4,3 代入 y=ax2−4ax+3a，
∴3=16a−16a+3a，
∴a=1，
∴ 抛物线的表达式为：y=x2−4x+3；
② 327. （1） ∵ 四边形 ABCD 是正方形，
∴∠DCB=90∘．
∴∠CDF+∠E=90∘．
∵BF⊥DE，
∴∠FBC+∠E=90∘．
∴∠FBC=∠CDF．
（2） ①
②猜想：数量关系为：BF=DF+CG．
证明：在 BF 上取点 M 使得 BM=DF 连接 CM．
∵ 四边形 ABCD 是正方形，
∴BC=DC．
∵∠FBC=∠CDF，BM=DF，
∴△BMC≌△DFC．
∴CM=CF，∠1=∠2．
∴△MCF 是等腰直角三角形．
∴∠MCF=90∘，∠4=45∘．
∵ 点 C 与点 G 关于直线 DE 对称，
∴CF=GF，∠5=∠6．
∵BF⊥DE，∠4=45∘，
∴∠5=45∘，
∴∠CFG=90∘，
∴∠CFG=∠MCF，
∴CM∥GF．
∵CM=CF，CF=GF，
∴CM=GF，
∴ 四边形 CGFM 是平行四边形，
∴CG=MF．
∴BF=DF+CG．
28. （1） F
（2） −3≤xP≤3 且 xP≠0．
（3） 4