初中数学北师大版九年级上册第四章 图形的相似7 相似三角形的性质学案及答案

这是一份初中数学北师大版九年级上册第四章 图形的相似7 相似三角形的性质学案及答案，共5页。学案主要包含了相似三角形与矩形，相似三角形与正方形，相似三角形与菱形等内容，欢迎下载使用。
教学过程
前课回顾
相似三角形的五种基本图形：
相似三角形的应用：
错题重现
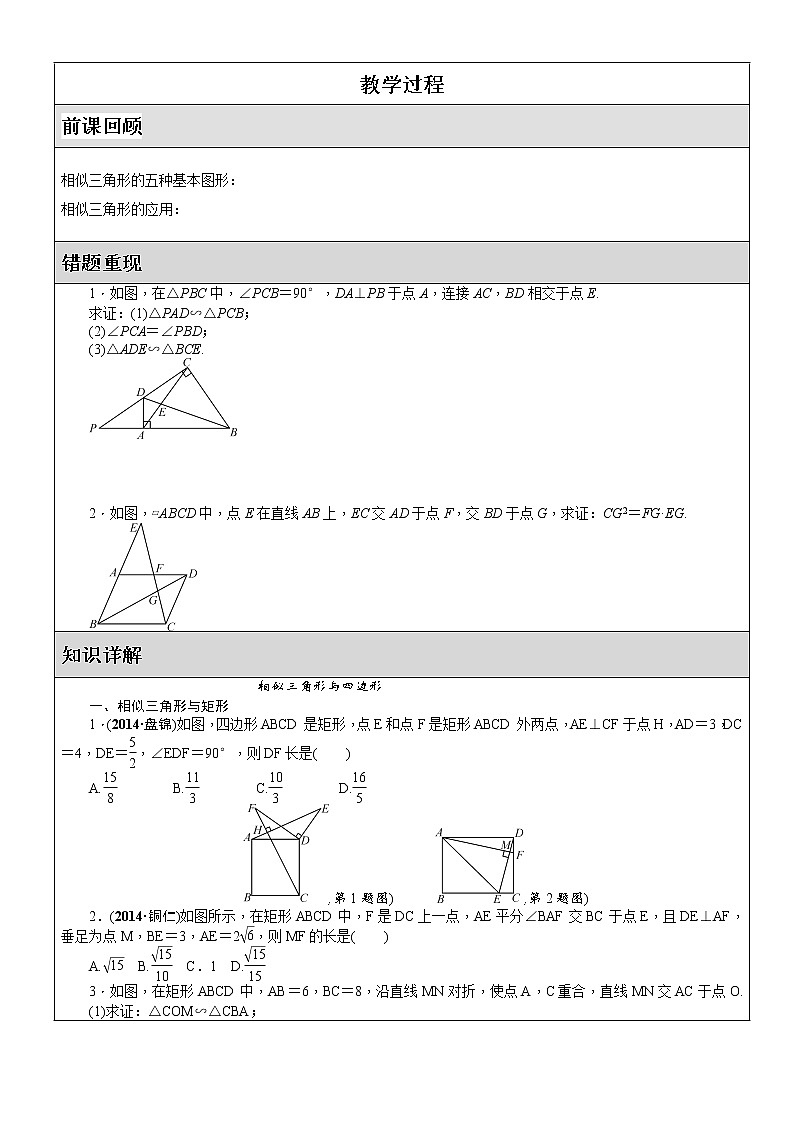
1．如图，在△PBC中，∠PCB＝90°，DA⊥PB于点A，连接AC，BD相交于点E.
求证：(1)△PAD∽△PCB；
(2)∠PCA＝∠PBD；
(3)△ADE∽△BCE.

2．如图，▱ABCD中，点E在直线AB上，EC交AD于点F，交BD于点G，求证：CG2＝FG·EG.
知识详解
相似三角形与四边形
一、相似三角形与矩形
1．(2014·盘锦)如图，四边形ABCD是矩形，点E和点F是矩形ABCD外两点，AE⊥CF于点H，AD＝3，DC＝4，DE＝eq \f(5,2)，∠EDF＝90°，则DF长是( )
A.eq \f(15,8) B.eq \f(11,3) C.eq \f(10,3) D.eq \f(16,5)
,第1题图) ,第2题图)
2．(2014·铜仁)如图所示，在矩形ABCD中，F是DC上一点，AE平分∠BAF交BC于点E，且DE⊥AF，垂足为点M，BE＝3，AE＝2eq \r(6)，则MF的长是( )
A.eq \r(15) B.eq \f(\r(15),10) C．1 D.eq \f(\r(15),15)
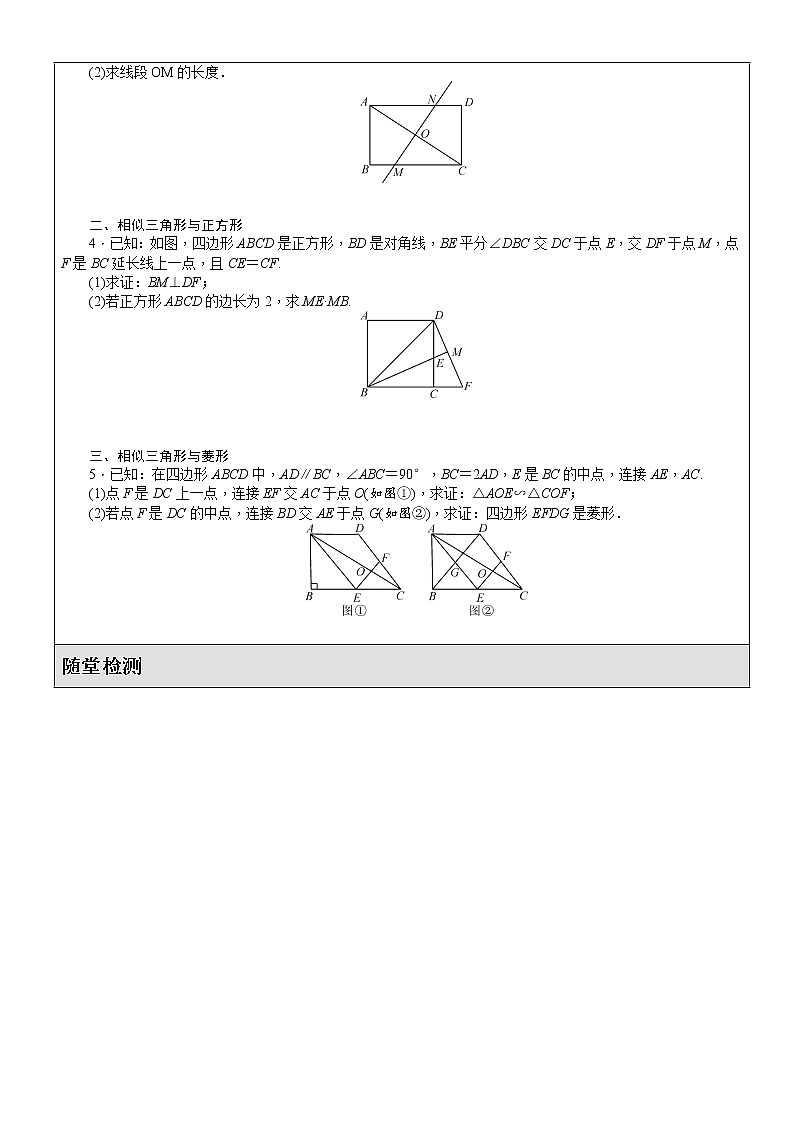
3．如图，在矩形ABCD中，AB＝6，BC＝8，沿直线MN对折，使点A，C重合，直线MN交AC于点O.
(1)求证：△COM∽△CBA；
(2)求线段OM的长度．

二、相似三角形与正方形
4．已知：如图，四边形ABCD是正方形，BD是对角线，BE平分∠DBC交DC于点E，交DF于点M，点F是BC延长线上一点，且CE＝CF.
(1)求证：BM⊥DF；
(2)若正方形ABCD的边长为2，求ME·MB.
三、相似三角形与菱形
5．已知：在四边形ABCD中，AD∥BC，∠ABC＝90°，BC＝2AD，E是BC的中点，连接AE，AC.
(1)点F是DC上一点，连接EF交AC于点O(如图①)，求证：△AOE∽△COF；
(2)若点F是DC的中点，连接BD交AE于点G(如图②)，求证：四边形EFDG是菱形．
随堂检测
一、选择题(本大题共8小题，每小题2分，共16分)
1．有同一个四边形地块的甲、乙两张地图，比例尺分别为1：30 000与1：50000，则甲地图与乙地图的相似比等于 ( )
A．3：5 B．5：3 C．： D．25：9
2．如果两个相似三角形的相似比是1：2，那么它们的面积比是 ( )
A．1：2 B．1：4 C 1： D．2：1
3．用幻灯机将一个三角形的面积放大为原来的900倍，下列说法正确的是 ( )
A．放大后是A、B、C原来的900倍
B．放大后周长是原来的30倍
C．放大后对应长是原来的900倍
D．放大后对应角平分线长是原来的900倍
4．下列4组条件中，能判定△ABC∽△DEF的是 ( )
A．AB=5，BC=4，A=650；DE=10，EF=8，D=650
B．A=550，B=550；D=550，F=800
C．AB=6，BC=5，B=800；DE=5，EF=4，E=800
D．BC=4，AC=6，AB=9；DE= 18，EF=8，DF=12
5．一个三角形三边之比为4：6：7，与之相似的另一个三角形最长边为28 cm，则其余两边之和为 ( )
A. 30 cm B．35 cm C．38 cm D．40 cm
6．如图是一个电脑桌面背景图，左右两个“京”字图的面积比约是 ( )
A．2：1 B．4：1 C．8：1 D．16：1
7．如图，AB∥CD，BO：OC=1：4，点E、F分别是OC、OD的中点，则EF：AB的值为 ( )
A．1 B．2 C．3 D．4
8．图为△ABC与△DEC重叠的情形，其中E在BC上，AC交DE于F点，且AB∥DE．若△ABC与△DEC的面积相等，且EF=9，AB=12，则DF为 ( )
A．3 B．7 C . 12 D．15
二、填空题(本大题共10小题，每小题2分，共20分)
9．已知4a=5b，则=__________，=__________．
10. 若点P把线段AB分成两段(AP>BP)．且满足PA2=PB·AB(即PA是PB和 AB的比例中项)，则称这种分割为__________．点P称为线段AB的黄金分割点，此时PA≈__________AB．
1l. 已知线段a=5 cm，b=2 cm，x又是线段a、b的比例中项，则x=__________．
12. 在比例尺为1：200的地图上，测得A，B两地面丽距离为4.5 cm，则A，B两地间的实际距离为__________m．
13. 在相同时刻，物高与影长成比例，如果高为1.5 m的标杆的影长为4 m，那么影长为40 m的旗杆的高度为__________．
14. △ABC中，AB=18，AC=16，D在AB上，AD=9，在AC上取一点P，问AP=__________时，以A、P、D为顶点的三角形与△ABC相似。
15. 如图。点D、E分别在△ABC的边AB、AC上，且AED=ABC，若DE=3，BC=6，AB=8，则AE的长为__________．
16. 如图，△ABC中，CDAB，垂足为D．下列条件中，能证明△ABC是直角三角形的有__________．①．A+B=900；②AB2=AC2+BC2；③；④CD2=ADBD．
17. 如图是一山谷的横断面示意图，宽AA'为15 m，用曲尺(两直尺相交成直角)从山谷两侧测量出OA=1 m，OB=3 m，O'A'=0.5 m，O'B'=3m(点A、O、O'、A'在同一条水平线上)则该山谷的深h为__________m．
18. 如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为__________．
三、解答题(本大题共10小题，共64分)
19. (本小题5分)如图，△AEB和△DEC相似吗?说明理由．
20. (本小题5分)在如图的网格中有一个格点三角形ABC，请在图中画一个与△ABC相似且相似比不等于1的格点三角形．
21．(本小题5分)已知△ABC，请以O为位似中心按3：2的位似比画出它的位似图形.
22．(本小题5分)在边长为2的菱形ABCD中，B=450，AE为BC 边上的高，将△ABE沿AE所在直线翻折得△AB'E，求△AB'E与四边形AECD重叠(阴影)部分的面积．
23．(本小题6分)如图所示，在一片空旷的地面上，矗立着一棵高大的松树，要测出它的高度．目前可供选用的工具有一根长3 m的竹竿、一把足够长的卷尺和一面镜子，请至少设计出两种不同的方案来测量树高(要求：写出设计方案，画出图形，不要求计算)．
24．(本小题6分)已知A、B、C、D点的坐标如图所示，E是图中两条虚线的交点，若△ABC和△ADE相似，求E点的坐标．
25．(本小题6分)如图，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．试说明．