高中数学人教版新课标A必修4第二章 平面向量2.5 平面向量应用举例背景图课件ppt

这是一份高中数学人教版新课标A必修4第二章 平面向量2.5 平面向量应用举例背景图课件ppt，共11页。
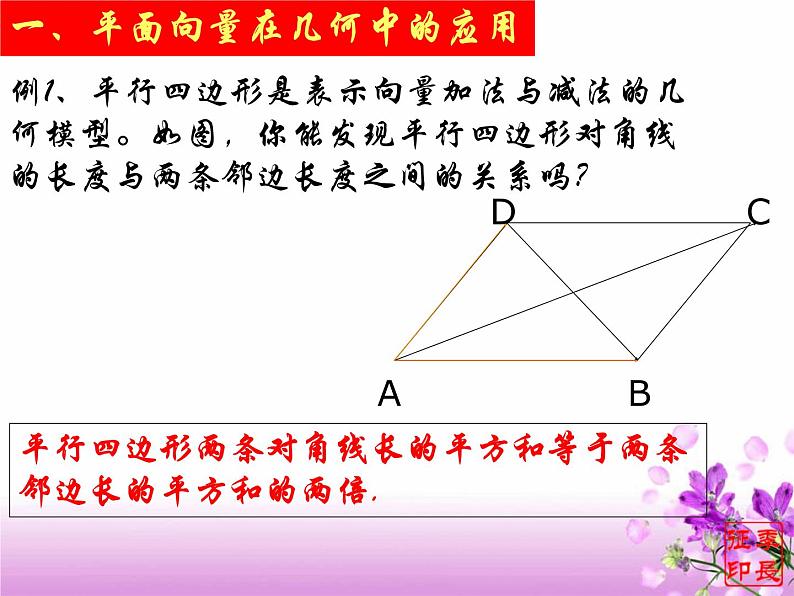
例1、平行四边形是表示向量加法与减法的几何模型。如图，你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗？
一、平面向量在几何中的应用
平行四边形两条对角线长的平方和等于两条邻边长的平方和的两倍.
（3）把运算结果“翻译”成几何元素。
用向量方法解决平面几何问题的“三步曲”：
（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；
（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题；
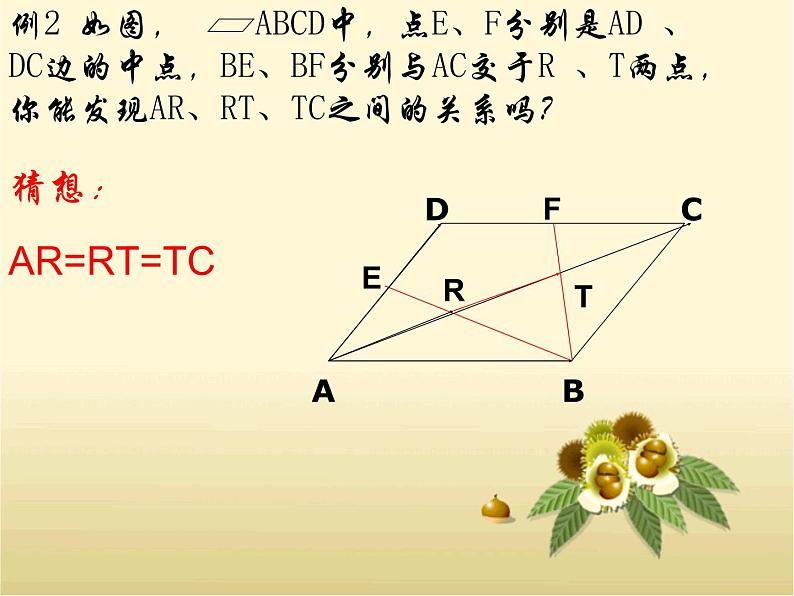
猜想：AR=RT=TC
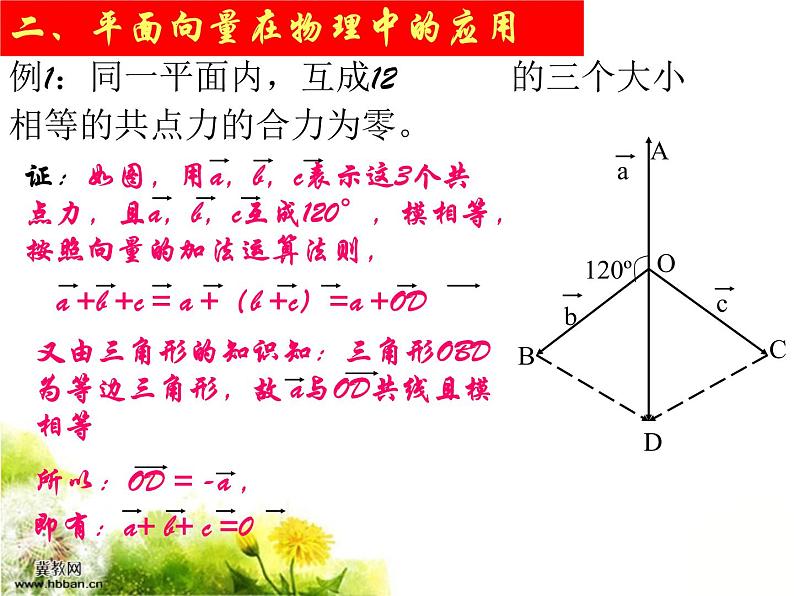
二、平面向量在物理中的应用
例1：同一平面内，互成120ْ 的三个大小相等的共点力的合力为零。
又由三角形的知识知：三角形OBD为等边三角形，故 a与OD共线且模相等所以：OD = -a ，
证：如图，用a，b，c表示这3个共点力，且a，b，c互成120°，模相等，按照向量的加法运算法则，
a +b +c = a +（b +c）=a +OD
即有：a+ b+ c =0
例2：在生活中，你是否有这样的经验：两个人共提一个旅行包，夹角越大越费力；在单杠上做引体向上运动，两臂夹角越小越省力！你能从数学的角度解释这个现象吗？
分析：上述的问题跟如图所示的是同个问题，抽象为数学模型如下：
用向量F1，F2，表示两个提力，它们的合向量为F，物体的重力用向量G来表示， F1，F2的夹角为θ，如右图所示，只要分清F，G和θ三者的关系，就得到了问题得数学解释！
通过上面的式子，有：当θ由0º到180º逐渐变大时， 由0º到90º逐渐变大， 的值由大逐渐变小，因此 由小逐渐变大，即F1 ，F2之间的夹角越大越费力，夹角越小越省力！
（2） 能等于 吗？为什么？
探究：（1）θ为何值时， 最小，最小值是多少？
例3：如图，一条河流的两岸平行，河的宽度d = 500m，一艘船从A处出发到河对岸。已知船的速度 =10km/h，水流的速度 = 2km/h。 问：（1）行驶航程最短时，所用的时间是多少？ （2）行驶时间最短时，所用的时间是多少？
把物理问题转化为数学模型为：