






初中数学鲁教版 (五四制)九年级上册5 确定二次函数的表达式课文ppt课件
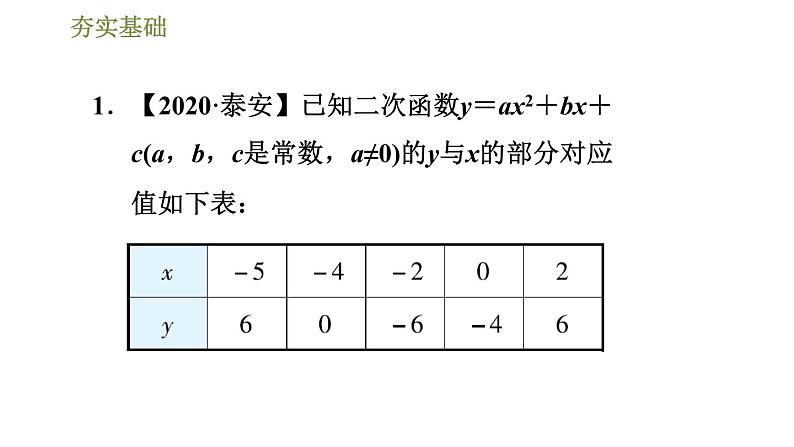
展开1.【2020·泰安】已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如下表:
下列结论:①a>0;②当x=-2时,函数最小值为-6;③若点(-8,y1),点(8,y2)在二次函数图象上,则y1
3.已知A(1,0),B(0,-1),C(-1,2),D(2,-1),E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中三个点.(1)求证:C,E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
证明:由题意可知,抛物线的对称轴为直线x=1.若点C(-1,2)在这个抛物线上,则C点关于直线x=1的对称点(3,2)也在这个抛物线上.∴C,E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上.
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
解:点A不在抛物线y=a(x-1)2+k(a>0)上.理由:若点A(1,0)在抛物线y=a(x-1)2+k(a>0)上,则k=0.∴y=a(x-1)2.易知B(0,-1),D(2,-1)都不在该抛物线上.由(1)知,C,E两点不可能同时在该抛物线上.∴与该抛物线经过其中三个点矛盾.∴点A不在该抛物线上.
4.【中考·宁波】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).(1)求抛物线的表达式和顶点坐标;
解:∵抛物线与x轴交于点A(1,0),B(3,0),∴抛物线的表达式为y=a(x-1)(x-3).把C(0,-3)的坐标代入,得3a=-3,解得a=-1,故抛物线的表达式为y=-(x-1)(x-3),即y=-x2+4x-3.∵y=-x2+4x-3=-(x-2)2+1,∴顶点坐标为(2,1).
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的表达式.
解:先向左平移2个单位,再向下平移1个单位,能使平移后的抛物线顶点落在直线y=-x上.平移后抛物线的表达式为y=-x2(答案不唯一).
解:y=3x2-6x+5可化为y=3(x-1)2+2,据对称可知:两图象关于x轴对称,所求表达式为y=-3(x-1)2-2,即y=-3x2+6x-5.
5. 已知二次函数y=3x2-6x+5,求满足下列条件的二次函数的表达式:(1)两图象关于x轴对称;
(2)两图象关于y轴对称;(3)两图象关于经过抛物线y=3x2-6x+5的顶点且平行于x轴的直线对称.
解:两图象关于y轴对称,所求表达式为y=3(x+1)2+2,即y=3x2+6x+5.
两图象关于经过抛物线y=3x2-6x+5的顶点且平行于x轴的直线对称,所求表达式为y=-3(x-1)2+2,即y=-3x2+6x-1.
6.【中考·宁波】已知抛物线y=(x-m)2-(x-m),其中m是常数.(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
证明:∵y=(x-m)2-(x-m)=(x-m)(x-m-1),∴由y=0得x1=m,x2=m+1.∵m≠m+1,∴不论m为何值,该抛物线与x轴一定有两个公共点:(m,0),(m+1,0).
7.【中考·菏泽】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.(1)试求抛物线的表达式;
(2)记抛物线顶点为D,求△BCD的面积;
初中数学人教版七年级上册1.2.4 绝对值优质课课件ppt: 这是一份初中数学人教版七年级上册1.2.4 绝对值优质课课件ppt,文件包含124《绝对值第1课时》课件-人教版数学七上pptx、124《绝对值第1课时》教案-人教版数学七上docx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
浙教版九年级上册1.1 二次函数精品ppt课件: 这是一份浙教版九年级上册1.1 二次函数精品ppt课件,共22页。PPT课件主要包含了学习目标,复习回顾,向上平移3个单位,y-2x2+3,向左平移2个单位,y-2x+22,先列表,知识精讲,顶点式,典例解析等内容,欢迎下载使用。
初中数学苏科版九年级上册1.2 一元二次方程的解法习题ppt课件: 这是一份初中数学苏科版九年级上册1.2 一元二次方程的解法习题ppt课件,共20页。PPT课件主要包含了答案呈现,习题链接,x=3a或x=-a等内容,欢迎下载使用。













