鲁教版 (五四制)九年级上册5 确定二次函数的表达式教学演示课件ppt

这是一份鲁教版 (五四制)九年级上册5 确定二次函数的表达式教学演示课件ppt，共27页。PPT课件主要包含了想一想，待定系数法，议一议，第二课时，确定二次函数的表达式，a-b+c，a+b+c，4a+2b+c，b-3，知识小结等内容，欢迎下载使用。

1.经历确定二次函数表达式的过程，体会求二次函数表达式的思想方法。2.会用待定系数法求二次函数表达式。3.能够灵活选择一般式，顶点式来确定二次函数表达式。
重点和难点：根据问题灵活选用二次函数表达式的不同形式。
1.二次函数表达式的一般形式是什么？
二次函数表达式的顶点式是什么？
3.若二次函数y=ax²+bx+c(a≠0)与x轴两交点为(x1，0)，(x2，0)则其函数表达式可以表示成什么形式？
y=ax²+bx+c (a，b，c为常数，a≠0)
y=a(x-h)2+k (a≠0)
y=a(x-x1)(x-x2) (a≠0)
如图，某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶。它的拱宽AB为6m，拱高CO为0.9m，试建立适当的直角坐标系，写出这段抛物线所对应的二次函数的表达式。
例1.已知一个二次函数的图象的对称轴为x=-2，与y轴交点的纵坐标为2，且经过点（-3，-1），求这个二次函数的表达式。
解：设二次函数表达式为y=ax2+bx+c(a≠0) ∵ 与y轴交点的纵坐标为2 ∴  c=2 ∴  y=ax2+bx+2 ∵ 图象的对称轴为x=-2 ∴  即b=4a ①    ∵二次函数的图象经过点（－3，－1）， ∴ 9a－3b+2=－1 ②由①②，解得，a=1，b=4 ∴  二次函数表达式为y=x2+4x+2 
如果二次函数y=ax2+bx+c的图象的顶点坐标为（h，k），那么这个二次函数的表达式可表示成什么形式？
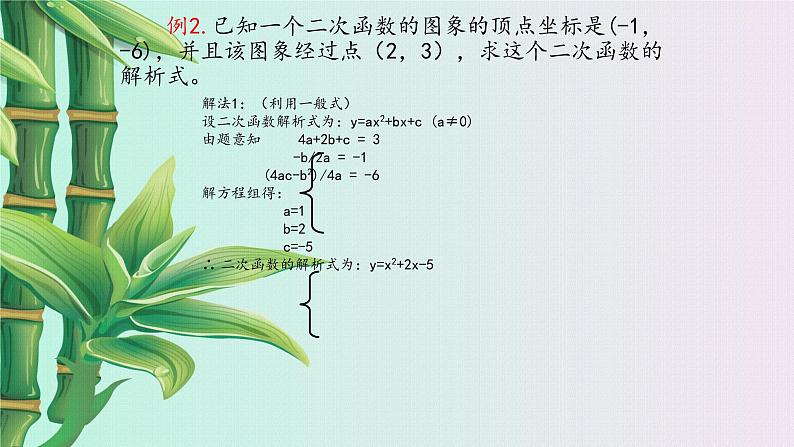
例2.已知一个二次函数的图象的顶点坐标是(-1，-6)，并且该图象经过点（2，3），求这个二次函数的解析式。
解法2：（利用顶点式）∵ 图象的顶点坐标是(-1，-6)∴可设二次函数得解析式为：   y=a(x+1)2-6∵  函数图象过点（2，3）∴  a(2+1)2-6=3∴  a=1∴ 二次函数的解析式为：y=(x+1)2-6
如图，某建筑的屋顶设计成横截面为抛物线（曲线AOB）的薄壳屋顶。它的拱宽AB为6m，拱高CO为0.9m。试建立适当的直角坐标系，并写出这段抛物线所对应的二次函数表达式？
解:以线段AB的中垂线为y轴，以过点O且与y轴垂直的直线为x轴，建立直角坐标系。
设它的函数表达式为: y=ax²(a≠0)
通过上述问题的解决，您能体会到求二次函数表达式采用的一般方法是什么？
你能否总结出上述解题的一般步骤？
1.若无坐标系，首先应建立适当的直角坐标系;2.设抛物线的表达式;3.写出相关点的坐标;4.列方程(或方程组);5.解方程或方程组，求待定系数;6.写出函数的表达式。
归纳： 在确定二次函数的表达式时（1）若已知三个非特殊条件，常设一般式；（2）若已知二次函数顶点坐标或对称轴，常设顶点式较为简便。
在确定二次函数的表达式时（1）若已知三个非特殊条件，常设一般式；（2）若已知二次函数顶点坐标或对称轴，常设顶点式较为简便。
确定二次函数的表达式的一般步骤：
想一想： 已知一个二次函数的图象所经过的3个点，可以确定这个二次函数的表达式吗？怎样确定这个二次函数的表达式？
例3：已知二次函数的图象经过(-1，10)，(1，4)，(2，7)，求这个函数的表达式。并写出它的对称轴和顶点坐标。
分析：要求二次函数的表达式，可设y=ax2+bx+c，然后一个点对应一个方程，列出三元一次方程组，求出a，b，c。
解：设所求二次函数的表达式为y=ax2+bx+c，
由已知，将三点(-1，10)，(1，4)，(2，7)分别代入表达式，得
故所求二次函数的表达式为y=2x2-3x+5
所以二次函数y=2x2-3x+5的对称轴为直线 ，顶点坐标为 。
解：（交点式）∵二次函数图象经过点(3，0)，(-1，0)∴设二次函数表达式为：y=a(x-3)(x+1) ∵ 函数图象过点(1，4)∴ 4=a(1-3)(1+1) 得a=-1∴ 函数的表达式为： y=-(x+1)(x-3) =-x2+2x+3
（补充）：已知二次函数图象经过点(1，4)，(-1，0)和(3，0)三点，求二次函数的表达式。
其它解法：（一般式）设二次函数解析式为y=ax2+bx+c∵二次函数图象过点(1，4)，(-1，0) 和(3，0)∴  a+b+c=4     ①    a-b+c=0     ②    9a+3b+c=0   ③ 解得：a= -1 b= 2 c= 3∴函数的解析式为：y=-x2+2x+3
（顶点式）解：∵  抛物线与x轴相交两点(-1，0)和(3，0) ，∴ (-1+3)/2 = 1∴ 点(1，4)为抛物线的顶点可设二次函数解析式为：y=a(x-1)2+4 ∵ 抛物线过点(-1，0)∴ 0=a(-1-1)2+4得a=-1∴ 函数的解析式为： y=-(x-1)2+4
综上解法比较可得：（1）若已知图象上三个非特殊点，常设一般式 ；（2）若已知二次函数与x轴的两个交点，常设交点式较为简单。
例3：已知二次函数的图象经过(－1，10)，(1，4)，(2，7)，求这个函数的表达式。并写出它的对称轴和顶点坐标。
例4：某商贸公司成立以来，5年的利润情况如下图所示，图中的折线近似于抛物线的一部分。
（1）试求出图象过A，C，D三点的二次函数的表达式；
解:设所求二次函数的表达式为y=ax2+bx+c，
由已知，将A(1，2.6)，C(3，3.8)，D(4，5)分别代入表达式，得
9a+3b+c=3.8
故所求二次函数的表达式为y=0.2x2-0.2x+2.6
（2）利用（1）的结果，分别求出当x=2和x=5时该二次函数的函数值，并分别与点B、点E的纵坐标比较。
解：当x=2时，y=0.2×4-0.2×2+2.6=3，
此时，y的值与点B的纵坐标相等。
当x=5时，y=0.2×25-0.2×5+2.6=6.6，
此时，y的值小于点E的纵坐标。
（3）利用（1）中求得的二次函数的表达式，预测该商贸公司第6年的利润。
解：当x=6时，y=0.2×36-0.2×6+2.6=8.6，
估计该商贸公司第6年的利润可达860万元。
归纳： 在确定二次函数的表达式时（1）若已知图像上三个非特殊点，常设一般式；（2）若已知二次函数顶点坐标或对称轴，常设顶点式较为简便；（3）若已知二次函数与x轴的两个交点，常设交点式较为简单。