

第8讲 复合应用题—小升初数学专题讲练(知识点+练习)(通用版,含详解)
展开小升初数学精讲精练专题汇编
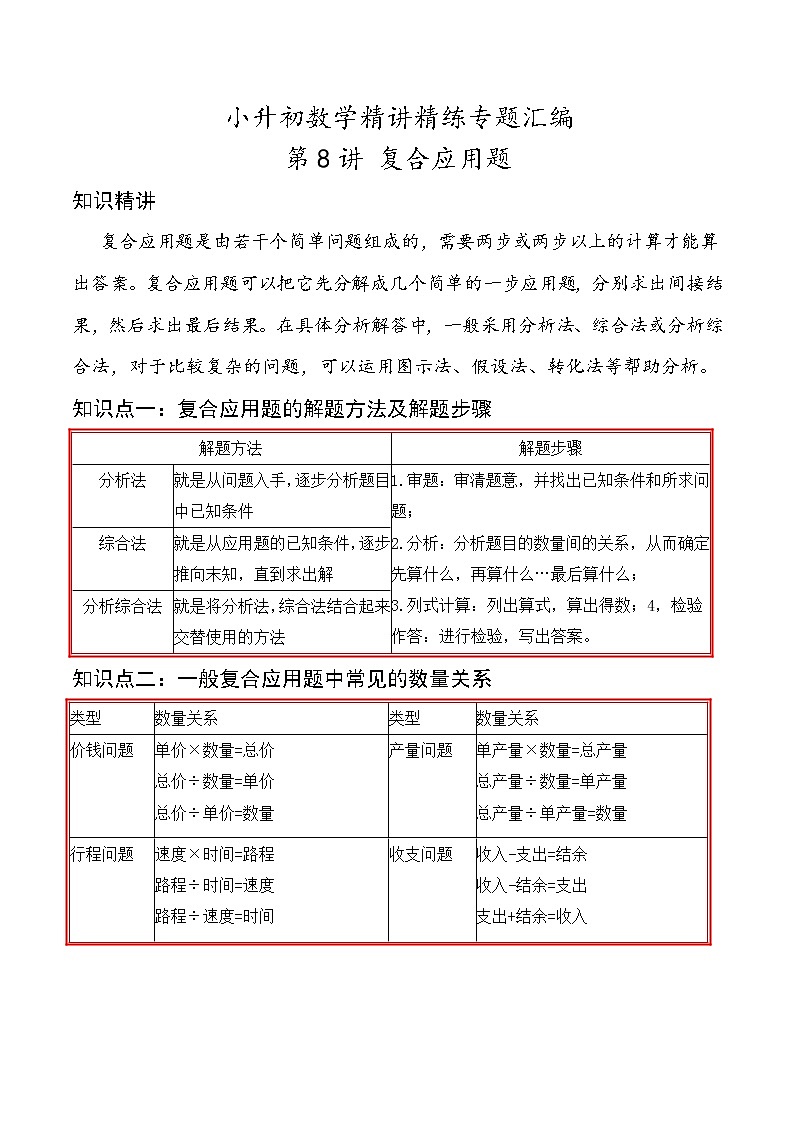
第8讲 复合应用题
知识精讲
复合应用题是由若干个简单问题组成的,需要两步或两步以上的计算才能算出答案。复合应用题可以把它先分解成几个简单的一步应用题,分别求出间接结果,然后求出最后结果。在具体分析解答中,一般采用分析法、综合法或分析综合法,对于比较复杂的问题,可以运用图示法、假设法、转化法等帮助分析。
知识点一:复合应用题的解题方法及解题步骤
解题方法 | 解题步骤 | |
分析法 | 就是从问题入手,逐步分析题目中已知条件 | 1.审题:审清题意,并找出已知条件和所求问题; 2.分析:分析题目的数量间的关系,从而确定先算什么,再算什么…最后算什么; 3.列式计算:列出算式,算出得数;4,检验作答:进行检验,写出答案。 |
综合法 | 就是从应用题的已知条件,逐步推向末知,直到求出解 | |
分析综合法 | 就是将分析法,综合法结合起来交替使用的方法 | |
知识点二:一般复合应用题中常见的数量关系
类型 | 数量关系 | 类型 | 数量关系 |
价钱问题 | 单价×数量=总价 总价÷数量=单价 总价÷单价=数量 | 产量问题 | 单产量×数量=总产量 总产量÷数量=单产量 总产量÷单产量=数量 |
行程问题 | 速度×时间=路程 路程÷时间=速度 路程÷速度=时间 | 收支问题 | 收入-支出=结余 收入-结余=支出 支出+结余=收入 |
工程问题 | 工作效率×工作时间=工作总量 工作总量÷工作时间=工作效率 工作总量÷工作效率=工作时间 | 打折问题 | 现价÷原价=折数 原价×折数=现价 现价÷折数=原价 |
知识点三:典型应用题
类型 | 特征 | 数量关系 | 关键点 | |
平均数问题 | 已知几个不相等的同类数量以及份数,求每份数 | 总数量÷总份数=平均数 | 找准总数量和总份数 | |
归一问题 | 题中每份的量保持不变,解题时先求出不变的单位量,再求未知量 | 总数量÷份数=单位量 单位量×单位量份数=总数量 总数量÷单位量=单位量份数 | 确定不变的每份量 | |
归总问题 | 题中的总量保持不变,解题时先求总量,再求未知量 | 每份量×份数=总数量 | 确定不变的总数量 | |
相遇问题 | 两个物体同时做相向运动,经过一段时间后在途中相遇 | 速度和×相遇时间=路程 路程÷速度和=相遇时间 路程÷相遇时间=速度和 | 弄清物体运动的方向和时间等 | |
追及问题 | 两个物体同时做同向运动,后者在一段时间内追及前者 | 路程差÷速度差=追及时间 速度差×追及时间=路程差[来源] 路程差÷追及时间=速度差 | 弄清物体运动的方向和时间等 | |
水中行船 问题 | 一般船是匀速运动,水速在船逆行和顺行中的作用不同 | 顺水速度=船速+水速 逆水速度=船速-水速 船速=(顺水速度+逆水速度)÷2 水速=(顺水速度-逆水速度)÷2 | 分清是顺水速度还是逆水速度 | |
过桥问题 | 涉及车长、桥长等问题 | 路程=桥长+车长 路程÷速度=时间 | 分清路程是否包含车长 | |
和差问题 | 已知两个量的和与差,求这两个量 | 较大数=(和十差)÷2 较小数=(和一差)÷2 | 移多补少 | |
和倍问题 | 已知两个量的差及两个量的倍数关系,求这两个量 | 和÷(倍数+1)=1倍的量 | 确定哪个量是1倍的量 | |
差倍问题 | 已知两个量的差及两个量的倍数关系,求这两个量 | 差÷(倍数-1)=1倍的量 | 确定哪个量是1倍的量 | |
年龄问题 | 有关人的岁数问题,常与和倍、差倍等问题结合在一起 | 参照和倍、差倍的数量关系 | 年龄差始终保持不变 | |
类型 | 特征 | 数量关系 | 关键点 | |
盈亏问题 | 一定数量的物品分成若干份,在不同的分配中,有余(盈)或不足 (亏),已知余或不足的数量,求物品的总数或份数 | (盈数+亏数)÷两次分得的差=份数 | 找出两次分得的差与盈亏的总数 | |
鸡兔同笼问题 | 已知鸡与兔的总头数和总腿数,求鸡与兔各有多少只的应用题 | 兔的只数=(总腿数-2×总头数)÷2 鸡的只数=(4×总头数-总腿数)÷2 | 假设法、方程法 | |
植树问题 | 不封闭 图形 | 两端都植树 | 棵数=段数+1 | 分清封闭还是不封闭,两端都植树还是都不植 |
两端都不植树 | 棵数=段数-1 | |||
封闭图形 | 在圆、正方形等边上植树 | 棵数=段数 | ||
说明:分数百分数应用题放在第10讲主讲;工程问题放在第11讲主讲;行程问题(相遇,追及,流水行船,火车过桥)放在第12讲主讲;列方程解应用题放在第8讲主讲,比和比例应用题放在第9讲主讲;经济问题放在第13讲主讲;本讲重点复习讲解平均数问题、归一归总问题、和差倍问题、盈亏问题、年龄问题、鸡兔同笼问题、植树问题
能力提升
一、精挑细选(共5题;每题2分,共10分)
1.(2020六上·南岗期末)学校小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的,如果他想买单价是2元的,可以买( )支。
A.4 B.3 C.2 D.1
2.(2020六上·龙岗期末)下面图中表示淘气爸爸在高速路上某段路程匀速行驶的是( )。
A. B.
C. D.
3.(2020六上·汝城期末)一段路,甲要9分钟走完,乙要12分钟走完,甲、乙两人的速度之比是( )。
A. B. C.
4.(2021六上·通榆期末)组装车间要装配两轮摩托车和三轮摩托车共21辆,需要51个轮胎,两轮摩托车和三轮摩托车的辆数分别是( )。
A.12和9 B.8和13 C.10和11 D.7和14
5.(2021六下·龙华月考)比例尺是1:4000000的地图上量得甲、乙两地相距24厘米,两火车同时从甲、乙两地相对开出,甲车每时行72千米,比乙车每时慢16千米,两车大约( )时后相遇。
A.4 B.5 C.6 D.7
二、判断正误(共5题;每题2分,共10分)
6.(2020六上·越城期末)走同一段路,甲需要3小时,乙需要4小时,甲、乙两人所需时间比是3:4,速度比是4:3。( )
7.小华4分钟写了88个毛笔字,小齐1分钟写了24个毛笔字,小华写得快.( )
8.耕两块同样大小的地,第一台拖拉机用了1 小时,第二台拖拉机用了1 小时.那么第一台拖拉机的工作效率高.( )
9.(2019六上·兴国期末)甲、乙两只蚂蚁分别沿着边长为2cm正方形和直径为2cm的圆走一圈,它们的速度一样,甲先爬行完一圈.( )
10.(2019·黔东南)3个外形、颜色都相同的小球,有一个与另外两个质量不同,用天平称1次,保证能把它找出来。( )
三、仔细想,认真填(共7题;每题1分共10分)
11.在比例尺为1:7500000的地图上,甲、乙两地的距离是6厘米,现有一辆客车和一辆货车同时从两地相对开出,经过3小时相遇,客车每小时行驶80千米,货车每小时行驶 千米。
12.(2021六下·古冶期中)一个圆柱和一个圆锥等底等高,它们的体积之差是36cm3。那么圆柱的体积是 cm3。
13.(2021六下·惠来期中)在一幅比例尺为1:4000000的地图上,量得甲、乙两地的距离是8厘米,甲、乙两地的实际距离是 千米,一辆汽车从甲地开往乙地,平均每小时行驶50千米, 小时到达。
14.(2021六下·宿迁月考)有76人去旅行,共租了8条船,大船限载12人,小船限载8人,这些船都坐满大船有 条,小船有 条。
15.(2021六下·淮安月考)今有鸡兔同笼,上有三十五头,下有九十四足,则鸡有 只,兔有 只。
16.(2020六上·大名期末)有24个外观完全一样的皮球,其中一个是不合格产品(轻或重不清楚),如果用天平称,至少称 次,能保证找到这个不合格的皮球。
17.(2020六上·鼓楼期中)搬运一个仓库的货物,甲需要10小时,乙需要12小时,丙需要15小时。有同样的仓库A和B,甲和丙在A仓库,乙在B仓库同时搬运货物,丙开始帮助甲搬运,中途又转向帮助乙搬运,最后同时搬完两个仓库的货物,丙帮助乙搬运了 小时。
四、解答题(共12题;共68分)
18.(5分)(2020·南关模拟)甲地到乙地的公路长250千米,一辆客车和一辆货车同时从甲地开往乙地,客车每小时行100千米,货车每小时行80千米。客车到达乙地时,货车离乙地还有多少千米?
19.(5分)两辆汽车同时从甲、乙两地出发,相向而行,3.2小时后在途中相遇。已知快车每小时行驶78千米,比慢车每小时多行16千米。甲、乙两地相距多少千米?
20.(5分)(2021·长春)小明家装修厨房需要用 480块某品牌的同一规格的瓷砖,“东方家园”出售的这种瓷砖有大、小两种包装,大包装每包 50 片,价格 30 元;小包装每包 30 片,价格为 20 元,若大、小包装均不拆开零售,那么怎样制定购买方案才能使所付费用最少?
21.(5分)(2021六下·龙华月考)在比例尺是1:6000000的地图上,量得两地之间的距离是12厘米,如果一辆汽车行完全程用7.2时,这辆汽车平均每时行多少千米?
22.(10分)(2021六下·沧州月考)某品牌的羽绒服搞促销活动,在A商场打七五折销售,在B商场按“每满100元减30元”的方式销售。妈妈要买一件标价1280的这种品牌的羽绒服。
(1)(5分)在A、B两个商场买,各应付多少钱?
(2)(5分)选择哪个商场更省钱?
23.(5分)(2021六下·宿迁月考)宿迁市实验学校的学生正在进行开外军训,晴天每天行20千米,雨天每天行10千米,8天一共行了140千米,这8天中有几天是晴天?有几天是雨天?
24.(5分)甲、乙两地相距270千米,一辆汽车从甲地开往乙地,又从乙地返回甲地,去时每小时行45千米,返回时每小时行54千米,求这辆汽车往返的平均速度.
25.(6分)(2021·宝塔)莎莎骑车到相距5千米的书店买书,买完书立刻返回家中。如图是她离开家的距离与时间的统计图。
(1)莎莎去书店每小时行 千米,用了 分钟,这段时间内她骑车的路程和时间成 比例。
(2)莎莎从书店返回家中的速度是每小时 千米,用了 分钟。
(3)莎莎返回时的速度比去时慢 %。
26.(5分)商店运进一种商品共400件,并确定了售价。如果按照售价的九折销售,全部卖出后,能得到6000元的利润。如果按照售价的八五折销售,全部卖出后,能得到2400元的利润。这件商品的售价是多少元?
27.(5分)某停车场收费标准如下:停车1小时内(包括1小时)收费5元,超过1小时的部分每0.5小时收费3元(不满0.5小时按0.5小时计算)。小明爸爸交了14元的停车费,他在停车场最多停了多长时间的车?
28.(6分)(2018六上·龙岗期中)一辆自行车的外轮胎直径是50厘米,如果每分钟转100周,要过一座942米长的桥,需要多少分钟?
29.(6分)(2018六上·未央期末)笑笑伞家5口人准备去某地旅游。甲旅行社的收费标准是:如果买了3张原价票,则其余的人按半价优惠;乙旅行社的收费标准是:家庭旅游按团体票售出,按原价的八五折优惠。这两家旅行社的原价都是每人1000元。笑笑家到哪个旅行社购票更省钱?
答案解析
1.【答案】B
【完整解答】1.5×4÷2
=6÷2
=3(只)
故答案为:B。
【思路引导】本题根据“总价=单价×数量”求出小明带的总钱数,再跟据“数量=总价÷单价”进行计算,据此即可求解。
2.【答案】C
【完整解答】解:表示匀速行驶的是C。
故答案为:C。
【思路引导】匀速行驶,也就是速度不变,那么时间与路程成正比。
3.【答案】B
【完整解答】解:甲、乙两人的速度之比=:
=(×36):(×36)
=4:3。
故答案为:B。
【思路引导】速度=路程÷时间,甲、乙两人的速度之比=:,再根据比的基本性质计算即可。
4.【答案】A
【完整解答】解:假设都是三轮车,则两轮摩托车有:
(21×3-51)÷(3-2)
=(63-51)÷1
=12(辆)
两轮车:21-12=9(辆)
故答案为:A。
【思路引导】假设都是三轮车,则轮胎数是63个,比52多,是因为把两轮车也当作三轮车来计算了,每辆两轮车多算了1个轮子,这样用一共多算的轮胎数除以每辆两轮车多算的轮胎数即可求出两轮车的辆数,进而求出三轮车的辆数。
5.【答案】C
【完整解答】解:24÷=96000000(厘米)
96000000厘米=960千米
72+16=88(千米)
960÷(72+88)
=960÷160
=6(小时)
故答案为:C。
【思路引导】两车的相遇时间=路程÷速度和;路程=图上距离÷比例尺。
6.【答案】(1)正
【完整解答】解:走同一段路,甲需要3小时,乙需要4小时,甲、乙两人所需时间比是3:4,速度比是4:3,说法正确。
故答案为:正确。
【思路引导】甲、乙两人所需要的时间之比=甲需要的时间:乙需要的时间;将总路程看作1,则甲、乙的速度之比=(路程÷甲需要的时间):(路程÷乙需要的时间),代入数值计算即可。
7.【答案】(1)错误
【完整解答】88÷4=22(个)
因为24>22,所以小齐写得更快些,原题说法错误。
故答案为:错误。
【思路引导】根据题意可知,要求谁写得快,先用除法求出小华的速度,然后对比即可解答。
8.【答案】(1)错误
【完整解答】解:1 小时>1 小时,即第二台拖拉机用的时间少,则它的工作效率高,原题说法错误。
故答案为:错误。
【思路引导】耕地面积相等,用的时间越少,工作效率越高,据此解答。
9.【答案】(1)错误
【完整解答】正方形的周长:2×4=8(cm);
圆的周长:3.14×2=6.28(cm);
6.28<8;
所以乙先爬行完一圈。
故答案为:错误。
【思路引导】根据题意,圆的周长C=πd,正方形的周长=边长×4,分别代入数值计算出圆的周长和正方形的周长,速度一定,路程越长,所需要的时间的越多,据此解答即可。
10.【答案】(1)错误
【完整解答】解: 3个外形、颜色都相同的小球,有一个与另外两个质量不同,用天平称2次,保证能把它找出来。 原题说法错误。
故答案为:错误。
【思路引导】由于不知道另外一个质量是重还是轻,所以1次不能保证找出。先把天平两端各放1个,如果平衡,剩下的那个就是质量不同的。如果不平衡,此时就不能确定哪个质量不同,需要把其中一个换成第三个,此时平衡,质量不同的就是换下的那个;不平衡,说明没有换的那个质量不同。
11.【答案】70
【完整解答】解:6÷
=6×7500000
=45000000(厘米)
=450(千米)
450÷3=150(千米)
150-80=70(千米)
故答案为:70。
【思路引导】实际距离=图上距离÷比例尺,实际距离÷相遇时间=客车和货车的速度和,客车和货车的速度和-客车速度=货车速度。
12.【答案】54
【完整解答】解:36÷(3-1)
=36÷2
=18(立方厘米)
18×3=54(立方厘米)
故答案为:54。
【思路引导】差倍问题的公式:差÷(倍数-1)=小数;小数×倍数=大数。等底等高的圆柱和圆锥,圆柱的体积的体积是圆锥体积的3倍,它们的体积差是36,据此解答。
13.【答案】320;6.4
【完整解答】解:甲、乙两地的实际距离=8÷(1:4000000)
=8×4000000
=32000000厘米
=320000米
=320千米;
所用时间=320÷50=6.4(小时)。
故答案为:320;6.4。
【思路引导】比例尺=图上距离:实际距离,所以实际距离=图上距离÷比例尺,代入数值 计算,再根据1千米=1000米=100000厘米将单位进行转化即可得出第一个空的答案;时间=路程÷速度,代入数值计算即可得出所用时间。
14.【答案】3;5
【完整解答】解:设大船有x条,小船有8-x条。
12×x+8×(8-x)=76
12x+64-8x=76
4x=12
x=3
所以大船有3条,小船有8-x=8-3=5条。
故答案为:3;5。
【思路引导】本题可以用方程作答,即设大船有x条,小船有8-x条,题中存在的等量关系是:大船限载的人数×租大船的条数+小船限载的人数×租小船的条数=一共有的人数,据此代入数据和字母作答即可。
15.【答案】23;12
【完整解答】解:假设全是兔,鸡:(35×4-94)÷(4-2)=46÷2=23只,兔:35-23=12只,所以鸡有23只,兔有12只。
故答案为:23;12。
【思路引导】假设全是兔,那么鸡的只数=(一共有头的个数×一只兔子有足的只数-一共有足的只数)÷每只鸡和兔的足数之差,进而求得兔的只数即可。
16.【答案】4
【完整解答】解:如果用天平称,至少称4次,能保证找到这个不合格的皮球。
故答案为:4。
【思路引导】先把这24个皮球平均分成3份,每份都是8个,将其中的2份分别放在天平的两端。
如果天平平衡,说明不合格的皮球在剩下的1份中,将天平一端的皮球拿出来,将剩下的1份儿放在天平的那端,此时可以确定不合格皮球的轻重;如果天平不平衡,将天平升高的那一端的八个皮球拿出来,将剩下的一份放在天平的那端。此时可以确定不合格皮球的轻重。假设这个不合格的皮球比合格的皮球轻一些。
然后将含有不合格的8个皮球。分成3个、3个、2个。将3个皮球的那两份分别放在天平的两端。如果天平平衡,那么不合格的那个皮球在剩下的2个中,把剩下的1个皮球分别在天平两端放一个,不合格的皮球就在天平上升的那一端;如果天平不平衡,不合格的皮球就在天平上升的那一端的3个中,将其中的2个皮球分别放在天平的两端。如果天平平衡,那么剩下的那1个皮球就是不合格的皮球。如果天秤不平衡,那么不合格的皮球就在天平上升的那一端。
17.【答案】5
【完整解答】解:甲、乙丙一共需要的时间=2÷(++)
=2÷(++)
=2÷
=8(小时),
(1-×8)÷
=÷
=5(小时)
所以丙帮乙搬运了5小时。
故答案为:5。
【思路引导】根据题意可得两个仓库搬运完一共需要的时间=2÷(甲的工作效率+乙的工作效率+丙的工作效率);丙帮乙搬运的时间=(1-乙的工作效率×乙一共搬运的时间)÷丙的工作效率,注意工作效率=工作总量÷工作时间,代入数值计算即可。
18.【答案】解:250-250÷100×80
=250-2.5×80
=250-200
=50(千米)
答:客车到达乙地时,货车离乙地还有50千米。
【思路引导】用总路程除以客车的速度求出客车到达时用的时间,用这个时间乘货车的速度求出货车行驶的路程,然后用总路程减去货车行驶的路程即可求出货车离乙地的距离。
19.【答案】解:(78-16+78)×3.2
=(62+78)×3.2
=140×3.2
=448(千米)
答:甲、乙两地相距448千米。
【思路引导】甲、乙两地的路程=速度和×相遇时间;其中,慢车的速度=快车的速度-16千米。
20.【答案】解:如果买大包装瓷砖:480÷50=9(包)……30(片),需要购买大包9包,小包1包需花费:9×30+20=290(元);
如买小包装瓷砖:480÷30=16(包),需花费:16×20=320(元);
290<320
答:购买大包装的瓷砖9包,小包装1包,这样所需费用最少。
【思路引导】30÷50=0.6(元),20÷30=0.66……(元),大包装便宜,所以尽量购买大包装。用总数除以大包装每包的片数,求出商和余数,商就是需要大包装的包数,余下的片数可以买小包装。这样是最便宜的方案。
21.【答案】解:12×6000000÷100000=720(千米)
720÷7.2=100(千米)
答:这辆汽车平均每时行100千米。
【思路引导】这辆汽车的速度=路程÷行驶的时间;其中,路程=图上距离÷比例尺。
22.【答案】(1)解:在A商场买:1280×75%=960(元);
在B商场买:1280里面含有12个100,减去12×30=360(元);
应付:1280-360=920(元)。
答:在A商场买,应付960元,在B商场买,应付920元。
(2)解:960>920。
答:选择B商场更省钱。
【思路引导】(1)在A商场买:标价×折扣=现价;在B商场买:先求出1280里面含有几个100,个数×30元=便宜的钱数,标价-便宜的钱数=应付的钱数;
(2)哪个花的钱少,选择那个商场更省钱。
23.【答案】解:假设全部是晴天
20×8=160(千米)
160-140=20(千米)
雨天20÷(20-10)=2(天)
晴天8-2=6(天)
答:有6天是晴天,2天雨天。
【思路引导】假设全是晴天,雨天的天数=(晴天每天行的距离×一共行的天数-实际一共行的距离)÷晴天每天和雨天每天行的距离之差,所以晴天的天数=一共行的天数-雨天的天数。
24.【答案】解:270×2÷(270÷45+270÷54)=540÷11≈49.09(千米/时)
答:这辆汽车往返的平均速度约是49.09千米/时。
【思路引导】往返路程÷往返时间=平均速度。
这是一道求平均速度的行程问题。要求往返的平均速度就是用往返的总路程作为总量,把往返的总时间作为总份数求解。
25.【答案】(1)10;30;正
(2)4;75
(3)60
【完整解答】解:(1)5÷=10千米,所以莎莎去书店每小时行10千米,用了30分钟,这段时间内她骑车的路程和时间成正比例;
(2)5÷=4千米,莎莎从书店返回家中的速度是每小时4千米,用了75分钟;
(3)(10-4)÷10=60%,所以莎莎返回时的速度比去时慢60%。
【思路引导】从图中可以看出,莎莎家到书店的距离是5千米;
(1)莎莎去书店每小时行的距离=莎莎家到书店的距离÷莎莎去时用的小时数;
速度一定,路程和时间成正比例;
(2)莎莎从书店返回家中的速度=莎莎家到书店的距离÷莎莎返回时用的小时数;
(3)莎莎返回时的速度比去时慢百分之几=(莎莎去时的速度-莎莎返回时的速度)÷莎莎去时的速度。
26.【答案】解:(6000-2400)÷400÷(90%-85%)
=3600÷400÷0.05
=9÷0.05
=180(元)
答:这件商品的售价是180元。
【思路引导】这件商品的售价=(九折销售获得的利润-八五折销售获得的利润)÷商品的总件数÷折扣差。
27.【答案】解:14-5=9(元)
(9÷3)×0.5
=3×0.5
=1.5(时)
1+1.5=2.5(时)
答:他在停车场最多停了2.5小时的车。
【思路引导】他在停车场最多停车的时间=超过1小时的费用÷单价×0.5+1小时内的费用。
28.【答案】解:3.14×50×100=15700(厘米/分钟)=157(米/分钟)
942÷157=6(分钟)
答:需要6分钟。
【思路引导】圆的周长:C=πd,时间=路程÷速度。
29.【答案】解:1000×3+1000÷2×2
=3000+1000
=4000(元)
1000×5x85%
=5000×85%
=4250(元)
答:笑笑到甲旅行社购票更省钱.
【思路引导】甲旅行社买3张原价票,买2张半价票,这样计算出甲旅行社的钱数;乙旅行社按照每人票价是1000元的85%计算出总价;比较后判断哪家根省钱即可.
第10讲 工程问题—小升初数学专题讲练(知识点+练习)(通用版,含详解): 这是一份第10讲 工程问题—小升初数学专题讲练(知识点+练习)(通用版,含详解),共22页。试卷主要包含了基本概念,基本关系,工程问题的类型和常用方法,解答问题等内容,欢迎下载使用。
第9讲 分数应用题—小升初数学专题讲练(知识点+练习)(通用版,含详解): 这是一份第9讲 分数应用题—小升初数学专题讲练(知识点+练习)(通用版,含详解),共20页。试卷主要包含了解决分数应用题的关键,单位“1”的标志与线索,“率”的寻找方法,常用数量关系式和解题模式,分数应用题的基本类型及方法,单位“1”的转化及应用等内容,欢迎下载使用。
第7讲 找规律—小升初数学专题讲练(知识点+练习)(通用版,含详解): 这是一份第7讲 找规律—小升初数学专题讲练(知识点+练习)(通用版,含详解),共21页。













