

浙江省杭州市2020-2021学年高二下学期期末教学质量检测数学试题+答案 (word版)
展开考生须知:
1. 本试卷分试题卷和答题卷两部分.满分150分,考试时间120分钟.
2. 请用黑色字迹的钢笔或签字笔在答题卡指定的区域(黑色边框)内作答,超出答题区域的作答无效!
3. 考试结束,只需上交答题卷.
一、选择题:本大题共15小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若集合,,则( )
A. B.
C. D.
2. 设函数,则( )
A. 2B. 3C. 4D. 5
3. ( )
A. B. -1C. D.
4. 已知,则“”是“”成立的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
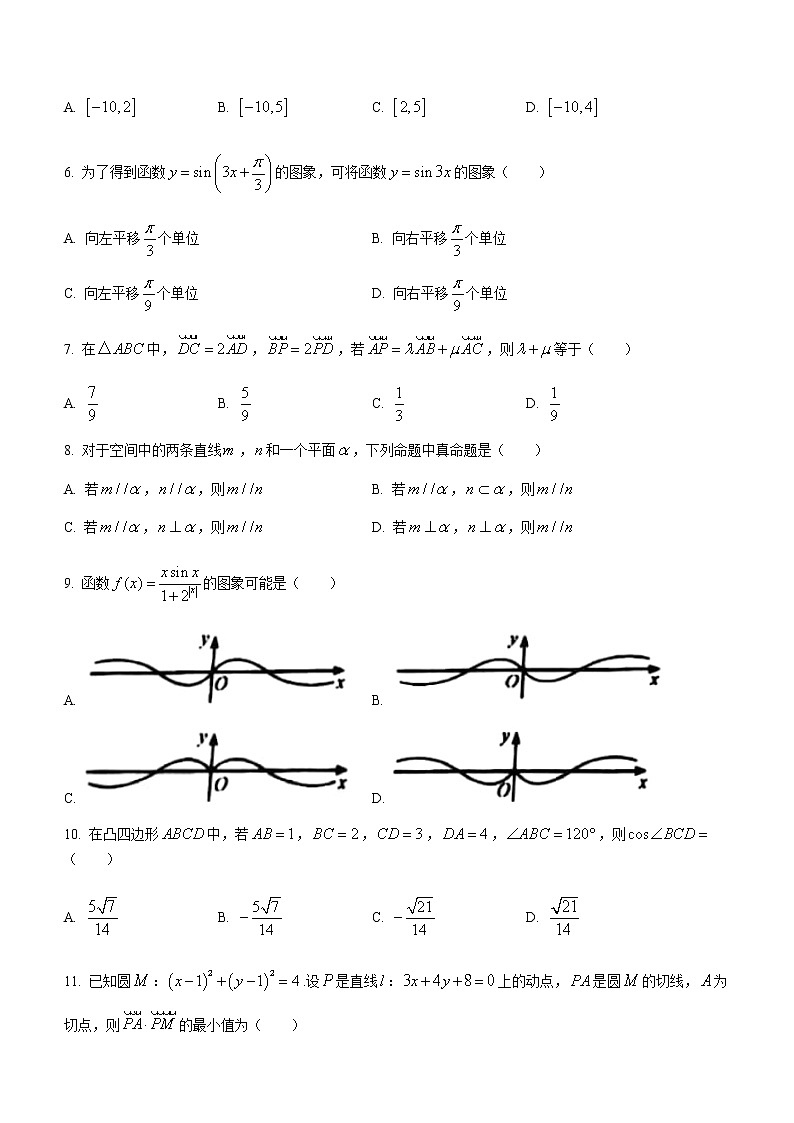
5. 若实数,满足,则的取值范围是( )
A. B. C. D.
6. 为了得到函数的图象,可将函数的图象( )
A. 向左平移个单位B. 向右平移个单位
C. 向左平移个单位D. 向右平移个单位
7. 在中,,,若,则等于( )
A. B. C. D.
8. 对于空间中的两条直线,和一个平面,下列命题中真命题是( )
A. 若,,则B. 若,,则
C. 若,,则D. 若,,则
9. 函数的图象可能是( )
A. B.
C. D.
10. 在凸四边形中,若,,,,,则( )
A. B. C. D.
11. 已知圆:.设是直线:上的动点,是圆的切线,为切点,则的最小值为( )
A. B. C. 3D. 5
12. 某几何体的三视图如图所示,则该几何体的体积是( )
A. B.
C. D.
13. 已知椭圆:的右焦点为,点,为第一象限内椭圆上的两个点,且,,则椭圆的离心率为( )
A. B. C. D. 2
14. 已知数列的前项和为,若,,则( )
A. B. C. D.
15. 设函数为单调函数,且时,均有,则( )
A. -3B. -2C. -1D. 0
二、填空题:本大题共4小题,每空4分,共16分.
16. 计算:__________.
17. 已知双曲线:的右焦点到渐近线的距离为4,则实轴长为___________.
18. 在锐角中,,,则的取值范围为__________.
19. 在四面体中,,,,,若四面体的外接球半径为,则四面体的体积的最大值为___________.
三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.
20. 已知函数.
(Ⅰ)若,且,求的值;
(Ⅱ)求函数的单调递增区间.
21. 已知为等差数列,是各项为正数且首项为2的等比数列,,,.
(Ⅰ)求和的通项公式;
(Ⅱ)求.
22. 如图,在三棱锥中,平面平面,,.
(Ⅰ)证明:;
(Ⅱ)求直线与平面所成角的正弦值.
23. 如图,过抛物线:的焦点作直线与交于,两点,与直线交于点().过点作的两条切线,切点分别为,.
(Ⅰ)证明:;
(Ⅱ)求四边形面积的最小值.
24. 设函数,,.
(Ⅰ)讨论函数在上的奇偶性;
(Ⅱ)设,若的最大值为,求的取值范围.
2020学年第二学期杭州市高二年级期末教学质量检测
数学参考答案及评分标准
一、选择题:本大题共15小题,每小题4分,共60分.在每小题给出的四个选项中只有一项是符合题目要求的.
二、填空题:本大题共4小题,每空4分,共16分.
16. 2 17. 6 18. 19.
三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.
20.(1)因为,,所以.
所以.
(Ⅱ)因为
,
由,,
得,.
所以的单调递增区间为,.
21.(Ⅰ)设等差数列的公差为,等比数列的公比为.
由已知,得,而,所以.
又因为,所以,所以,.
由,可得①.
由,可得②,
联立①②,解得,,由此可得.
所以数列的通项公式为,数列的通项公式为.
(Ⅱ)
.
22. 解法一:(Ⅰ)证明:在平面上过作于点,连接,
因为平面平面,所以平面,所以,
因为,所以,又因为,
所以,即,所以平面,
所以,所以.
(Ⅱ)直线与平面所成角也就是与平面所成角.
由(Ⅰ)知平面,所以平面平面,
过作于,则平面,
在直角三角形中,得,
所以直线与平面所成角的正弦为.
解法二:(Ⅰ)如图建立空间直角坐标系,设,
则,,,
,
∴,∴.
(Ⅱ)设,设平面的法向量,
由,即,
所以平面的一个法向量为,
设所求线面角为,则.
23.(1)设,,,过点切线斜率为,
则点切线方程为,联立
得,由得,
所以的切线方程,同理的切线方程,
代入点得,所以直线的方程为,
即,因为,所以.
(Ⅱ)设直线:,代入得,
设点,,则,,所以
,
同理,所以四边形的面积为
,
当时取到最小值.
24.(Ⅰ)当时,函数为奇函数.
当时,函数既不是奇函数也不是偶函数.
(Ⅱ)设.
①当时,,所以在递减,
,,
,所以,
,解得.
所以.
②当时,,所以在递增,在递减,
又,,,
,,
所以,又,
所以,
,
又,所以,同时,所以,
由在递增,所以.
综上,当时,;当时,.
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
D
C
A
A
B
C
B
D
C
C
D
D
C
B
D
浙江省杭州市2020-2021学年下学期高三年级教学质量检测(二模)数学试题(含答案 ): 这是一份浙江省杭州市2020-2021学年下学期高三年级教学质量检测(二模)数学试题(含答案 ),共8页。
浙江省杭州市2022-2023学年高三数学下学期教学质量检测(二模)试题(Word版附答案): 这是一份浙江省杭州市2022-2023学年高三数学下学期教学质量检测(二模)试题(Word版附答案),共8页。试卷主要包含了 本试卷分试题卷和答题卷两部分, 考试结束,只需上交答题卡, 设平面向量,,且,则, 某兴趣小组研究光照时长x, 已知,,且,则ab的最小值为, 若直线与圆C等内容,欢迎下载使用。
2019-2020学年浙江省杭州市高一下学期期末教学质量检测数学试题 PDF版: 这是一份2019-2020学年浙江省杭州市高一下学期期末教学质量检测数学试题 PDF版,共7页。












