陕西省西安市2020-2021学年八年级下学期数学期末综合练习测试卷（word版 含答案）

这是一份陕西省西安市2020-2021学年八年级下学期数学期末综合练习测试卷（word版 含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共40分）
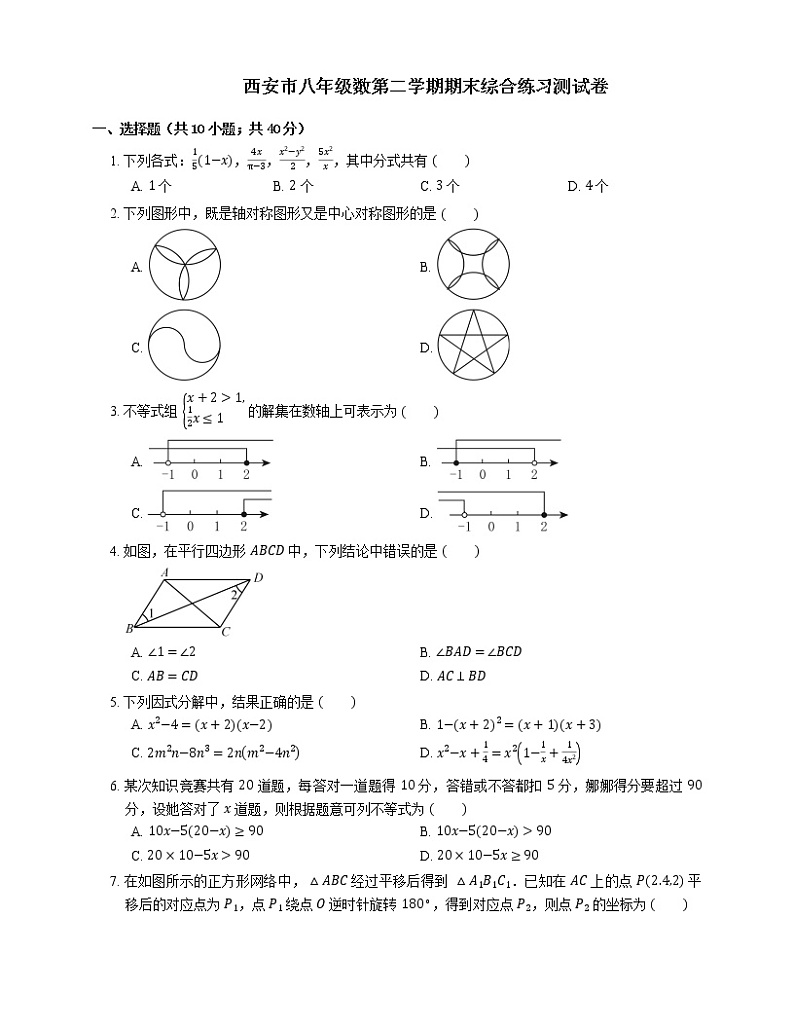
1. 下列各式：151−x，4xπ−3，x2−y22，5x2x，其中分式共有
A. 1 个B. 2 个C. 3 个D. 4 个

2. 下列图形中，既是轴对称图形又是中心对称图形的是
A. B.
C. D.

3. 不等式组 x+2>1,12x≤1 的解集在数轴上可表示为
A. B.
C. D.

4. 如图，在平行四边形 ABCD 中，下列结论中错误的是
A. ∠1=∠2B. ∠BAD=∠BCD
C. AB=CDD. AC⊥BD

5. 下列因式分解中，结果正确的是
A. x2−4=x+2x−2B. 1−x+22=x+1x+3
C. 2m2n−8n3=2nm2−4n2D. x2−x+14=x21−1x+14x2

6. 某次知识竞赛共有 20 道题，每答对一道题得 10 分，答错或不答都扣 5 分，娜娜得分要超过 90 分，设她答对了 x 道题，则根据题意可列不等式为
A. 10x−520−x≥90B. 10x−520−x>90
C. 20×10−5x>90D. 20×10−5x≥90

7. 在如图所示的正方形网络中，△ABC 经过平移后得到 △A1B1C1．已知在 AC 上的点 P2.4,2 平移后的对应点为 P1，点 P1 绕点 O 逆时针旋转 180∘，得到对应点 P2，则点 P2 的坐标为
A. 1.4,−1B. 1.5,2C. 1.6,1D. 2.4,1

8. 某生态示范园，计划种植一批核桃，原计划总产量达 36 万 kg，为了满足市场需求，现决定改良核桃品种，改良后平均每亩产量是原计划的 1.5 倍，总产量比原计划增加了 9 万 kg，种植亩数减少了 20 亩，则原计划和改良后平均每亩产量各为多少万千克?设原计划平均每亩产量为 x 万 kg，则改良后平均每亩产量为 1.5x 万 kg，根据题意列方程为
A. 36x−36+91.5x=20B. 36x−361.5x=20
C. 36+91.5x−36x=20D. 36x+36+91.5x=20

9. 如图，在平行四边形 ABCD 中，∠B=60∘，将 △ABC 沿对角线 AC 折叠，点 B 的对应点落在点 E 处，且点 B,A,E 在一条直线上，CE 交 AD 于点 F．则图中等边三角形共有
A. 4 个B. 3 个C. 2 个D. 1 个

10. 如图，△ABC 是等边三角形，P 是 ∠ABC 的平分线 BD 上一点，PE⊥AB 于点 E，线段 BP 的垂直平分线交 BC 于点 F，垂足为点 Q．若 BF=2，则 PE 的长为
A. 2B. 23C. 3D. 3
二、填空题（共7小题；共28分）
11. 计算：2xx2−y2−2yx2−y2= ．

12. 若 n 边形内角和是 900∘，则边数 n= ．

13. 如图，在 Rt△ABC 中，∠BAC=90∘，AB=8，AC=6，DE 是 AB 边的垂直平分线，垂足为 D，交边 BC 于点 E，连接 AE，则 △ACE 的周长为 ．

14. 如图，将 △ABC 绕着点 C 按顺时针方向旋转 20∘，B 点落在 Bʹ 的位置，A 点落在 Aʹ 的位置，若 AC⊥AʹBʹ，则 ∠BAC= ．

15. 一个圆环，外圆的半径为 R，内圆的半径为 r．当 R=15.25 cm，r=5.25 cm 时，圆环的面积约是 （π 取 3.14，结果精确到 1 cm2）．

16. 对于实数 x，我们规定 x 表示不大于 x 的最大整数，例如 1.2=1，3=3，−2.5=−3，若 x+410=5，则 x 的取值范围是 ．

17. 已知关于 x 的方程 2x+mx−2=3 的解是正数，在 m 的取值范围为 ．
三、解答题（共7小题；共84分）
18. 把下列各式因式分解：
（1）m+n3+2mm+n2+m2m+n；
（2）a2+b22−4a2b2．

19. 先化简，再求值：x2x2−1÷1x−1+1，其中 x 是 5 的整数部分．

20. 解不等式组 3x−2≥x−4, ⋯⋯①2x+13>x−1, ⋯⋯② 并写出它所有的整数解．

21. 在平面直角坐标系中，O 为坐标原点．
（1）已知点 A3,1，连接 OA，作如下探究：
探究一：平移线段 OA，使点 O 落在点 B，设点 A 落在点 C，若点 B 的坐标为 1,2，请在图①中作出 BC，点 C 的坐标是 ；
探究二：将线段 OA 绕点 O 逆时针旋转 90∘，设点 A 落在点 D，则点 D 的坐标是 ，连接 AD，则 AD= （图②为备用图）；
（2）已知四点 O0,0，Aa,b，C，Bc,d，顺次连接 O，A，C，B，若所得到的四边形为平行四边形，则点 C 的坐标是 ．

22. 某服装店老板用 4500 元购进一批衬衫，很快售完，服装店老板又用 2100 元购进第二批该款式的衬衫，进货量是第一批的一半，但进价每件比第一件降低了 10 元．
（1）这两批各购进这种衬衫多少件?
（2）若第一批衬衫的售价是 200 元 / 件，老板想让这两批衬衫售完后的总利润不低于 1950 元，则第二批衬衫每件至少要售多少元?

23. 两个全等的直角三角形重叠放在直线 l 上，如图①所示，AB=6 cm，AC=10 cm，∠ABC=90∘，将 Rt△ABC 在直线 l 上左右平移（如图②）．
（1）求证：四边形 ACFD 是平行四边形．
（2）怎样移动 Rt△ABC，使得四边形 ACFD 的面积等于 △ABC 的面积的一半?
（3）将 Rt△ABC 向左平移 4 cm，求四边形 DHCF 的面积．

24. 点 D 是等边三角形 ABC 外一点，且 DB=DC，∠BDC=120∘，将一个三角尺 60∘ 的顶点放在点 D 上，三角尺的两边 DP，DQ 分别于射线 AB，CA 相交于 E，F 两点．
（1）当 EF∥BC 时，如图①所示，求证：EF=BE+CF；
（2）当三角尺绕点 D 旋转到如图②所示的位置时，线段 EF，BE，CF 之间的上述数量关系是否成立?如果成立，请说明理由；如果不成立，写出 EF，BE，CF 之间的数量关系，并说明理由．
（3）当三角尺绕点 D 继续旋转到如图③所示的位置时，（1）中的结论是否发生变化?如果不变化，直接写出结论；如果变化，请直接写出 EF，BE，CF 之间的数量关系．
答案
1. A
2. B
3. A
4. D【解析】∵ 在平行四边形 ABCD 中，∴ AB∥CD，∴ ∠1=∠2，故A选项正确，不合题意；∵ 四边形 ABCD 是平行四边形，∴ ∠BAD=∠BCD，AB=CD，故B，C选项正确，不合题意；无法得出 AC⊥BD，故此选项错误，符合题意．
5. A
6. B【解析】∵ 每答对一道题得 10 分，答错或不答都扣 5 分，∴ 答对了 x 道题的得分为 10x 分，答错或不答的题目共有 20−x 道，共扣 520−x 分，从而由娜娜得分要超过 90 分可列不等式为 10x−520−x>90．
7. C【解析】根据图形中一个点确定平移方向，可计算 P1 的坐标，绕点 O 逆时针旋转 180∘ 即关于原点对称，根据关于原点对称的点的坐标规律确定 P2 点的坐标．
8. A
9. B【解析】本题分析如下：等边三角形 理由△BCE∵△ABC 沿对角线 AC 折叠,点 B,A,E 在一条直线上,∴△ABC≌△AEC,∠E=∠B=60∘,∴△BCE是等边三角形△EAF∵△AD∥BC,∴∠EAF=∠B=60∘,∴△EAF是等边三角形△DCF∵BE∥CD,∴∠D=∠EAF=60∘,∠E=∠DCF=60∘,∴△CDF 是等边三角形
10. C
【解析】∵△ABC 是等边三角形，BD 平分 ∠ABC，∴∠DBA=∠DBC=30∘．
∵QF 垂直平分 BP，∴BP=2BQ，且 ∠BQF=90∘．
在 Rt△BFQ 中，FQ=12BF=1，BQ=BF2−FQ2=22−12=3．
于是 BP=23．
在 Rt△BPE 中，PE=12BP=3．
11. 2x+y
12. 7
13. 16
【解析】在 Rt△ABC 中，∠BAC=90∘，AB=8，AC=6，利用勾股定理即可求得 BC 的长．又由 DE 是 AB 边的垂直平分线，根据线段垂直平分线的性质，即可得 AE=BE，继而可得 △ACE 的周长为：BC+AC=16．
14. 70∘
15. 644 cm2
16. 46≤x<56
17. m>−6 且 m≠−4
【解析】去分母得 2x+m=3x−2，解得 x=m+6，
∵ 原方程的解是正数，∴m+6>0，∴m>−6．
又 ∵x≠2，∴m+6≠2．
∴m≠−4．
故此题答案为 m>−6 且 m≠−4．
18. （1） m+n3+2mm+n2+m2m+n=m+nm+n2+2mm+n+m2=m+n2m+n2.
（2） a2+b22−4a2b2=a2+b22−2ab2=a2+b2+2aba2+b2−2ab=a+b2a−b2.
19. 原式=x2x2−1÷xx−1=x2x+1x−1⋅x−1x=xx+1.
∵x 是 5 的整数部分，
∴x=2．
当 x=2 时，原式=22+1=23．
20. 由 ① 得
3x−6≥x−4,
即
2x≥2.
解得
x≥1.
由 ② 得
2x+1>3x−3,
即
−x>−4.
解得
x<4.∴
原不等式组的解集是 1≤x<4．
∴ 原不等式组的所有的整数解是 1，2，3．
21. （1） 探究一：4,3；作图如图①所示．
探究二：−1,3；25．点 D 的坐标是 −1,3，如图②，AD=22+42=25．
（2） a+c,b+d．
∵ 四点 O0,0，Aa,b，C，Bc,d，
顺次连接 O，A，C，B 所得到的四边形为平行四边形，
∴OA∥BC 且 OA=BC．
∴ 可以看做是把 OA 平移到 BC 的位置．
∴ 点 C 的坐标为 a+c,b+d．
22. （1） 设第一批衬衫每件进价是 x 元，则第二批每件进价是 x−10 元，根据题意可得：
4500x×12=2100x−10.
解得
x=150.
经检验，x=150 是原方程的解，且符合题意．
4500150=30（件），2100150−10=15（件）．
答：第一批衬衫进了 30 件，第二批进了 15 件．
（2） 设第二批衬衫每件的售价为 y 元，根据题意可得：
30×200−150+15y−140≥1950.
解得
y≥170.
答：第二批衬衫每件至少要售 170 元．
23. （1） ∵ 四边形 ACFD 是由 Rt△ABC 平移形成的，
∴AD∥CF，AC∥DF，
∴ 四边形 ACFD 为平行四边形．
（2） 由题得 BC=102−62=8cm，△ABC的面积=24cm2．
要使得四边形 ACFD 的面积等于 △ABC 的面积的一半，
即 6×CF=24×12，
解得 CF=2 cm，
∴ 将 Rt△ABC 向左（或右）平移 2 cm，可使四边形 ACFD 的面积等于 △ABC 的面积的一半．
（3） 将 Rt△ABC 向左平移 4 cm，则 BE=AD=4 cm．
又 ∵BC=8 cm，∴CE=4 cm=AD．
∵AD∥BF，
∴∠HAD=∠HCE．
又 ∵∠DHA=∠EHC，
∴△DHA≌△EHC．
∴DH=HE=12DE=3 cm．
∴△HEC 的面积为 6 cm2．
∴ 四边形 DHCF 的面积为 S△ABC−S△HEC=24−6=18cm2．
24. （1） ∵△ABC 是等边三角形，
∴AB=AC，∠ABC=∠ACB=60∘．
∵DB=DC，∠BDC=120∘，
∴∠DBC=∠DCB=30∘．
∴∠DBE=∠DBC+∠ABC=90∘，
∠DCF=∠DCB+∠ACB=90∘．
∵EF∥BC，
∴∠AEF=∠ABC=60∘，∠AFE=∠ACB=60∘．
∴AE=AF．
∴BE=AB−AE=AC−AF=CF．
又 ∵DB=DC，∠DBE=∠DCF，
∴△BDE≌△CDF．
∴DE=DF，∠BDE=∠CDF=30∘．
∴BE=12DE=12DF=CF．
∵∠EDF=60∘，
∴△DEF 是等边三角形，即 DE=DF=EF．
∴BE+CF=12DE+12DF=EF，即 EF=BE+CF．
（2） 结论仍然成立．
理由：如图，在 AB 的延长线上取点 Fʹ，使 BFʹ=CF，连接 DFʹ．
由（1）得 ∠DBE=∠DCF=90∘，则 ∠DBFʹ=∠DCF=90∘．
又 ∵BD=CD，
∴△DCF≌△DBFʹSAS．
∴DF=DFʹ，∠BDFʹ=∠CDF．
又 ∵∠BDC=120∘，∠EDF=60∘，
∴∠EDB+∠CDF=60∘．
∴∠EDB+∠BDFʹ=∠EDFʹ=60∘．
又 ∵DE=DE，
∴△EDFʹ≌△EDFSAS．
∴EF=EFʹ=BE+BFʹ=BE+CF．
（3） 结论发生变化．EF=CF−BE．