人教版七年级上册2.2 整式的加减课文配套课件ppt

这是一份人教版七年级上册2.2 整式的加减课文配套课件ppt，共23页。PPT课件主要包含了学习目标，新课引入，知识讲解，352t，认识同类项，1“两相同”，①所含字母相同，2“两无关”，①与系数无关，活学活用等内容，欢迎下载使用。

1.掌握同类项、合并同类项的概念.2.掌握合并同类项的法则，能正确合并同类项．3.能先合并同类项化简后求值．
青藏铁路线上，在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100千米每时，在非冻土地段的行驶速度可以达到120千米每时，请根据这些数据回答下列问题：　　在西宁到拉萨路段，列车通过非冻土地段所需时间是通过冻土地段所需时间的2.1倍，如果通过冻土地段需要t小时，能用含t的式子表示这段铁路的全长吗？
解：这段铁路的全长（单位：千米）是 100t+120×2.1t， 即100t+252t.
类比数的运算，化简100t+252t.
(1) 运用有理数的运算律计算: 100×2+252×2=_________, 100×(-2)+252×(-2)=_________.(2) 根据(1)中的方法完成下面的运算： 100t+252t= .
解:(1)根据有理数的分配律可得100×2+252×2= (100+252) ×2 =704,100×(-2)+252×(-2)= (100+252) ×(-2) =-704.
观察算式(2)： 100t+252t
=(100+252)t
与(1)中算式结构相同
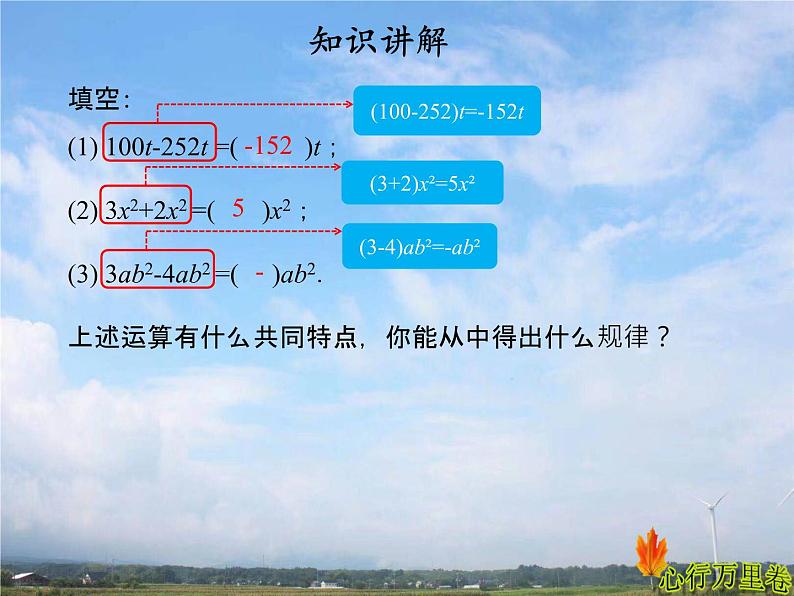
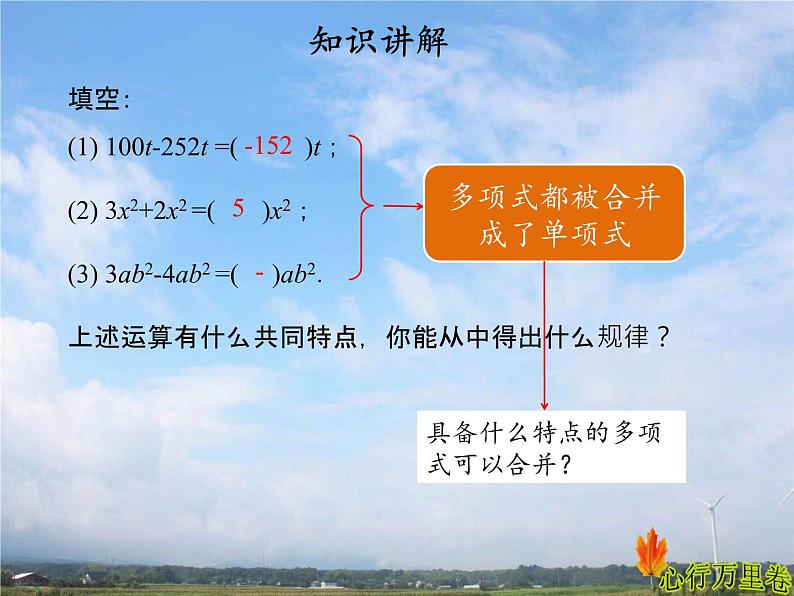
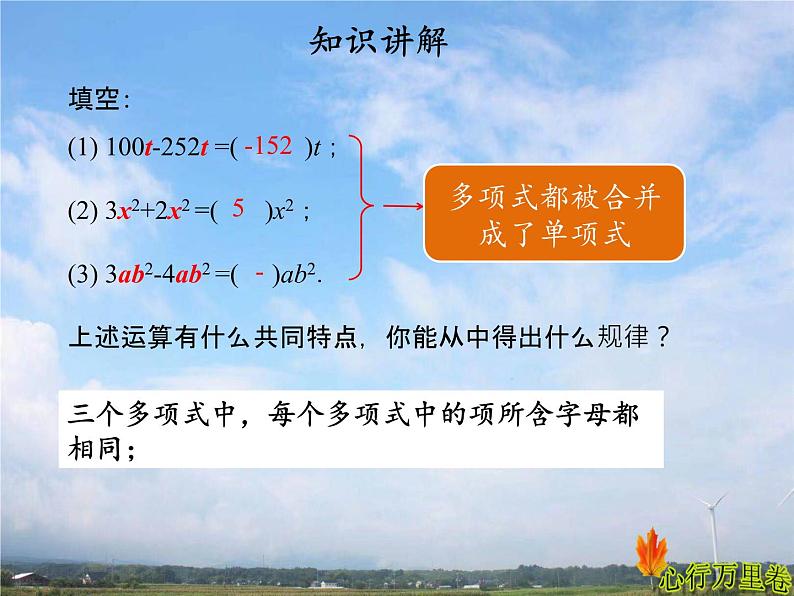
填空: (1) 100t-252t =( )t；(2) 3x2+2x2 =( )x2；(3) 3ab2-4ab2 =( )ab2．上述运算有什么共同特点，你能从中得出什么规律？
(100-252)t=-152t
(3+2)x²=5x²
(3-4)ab²=-ab²
多项式都被合并成了单项式
具备什么特点的多项式可以合并？
三个多项式中，每个多项式中的项所含字母都相同；
填空: (1) 100t1-252t 1=( )t；(2) 3x2+2x2 =( )x2；(3) 3ab2-4ab2 =( )ab2．上述运算有什么共同特点，你能从中得出什么规律？
每个多项式中，相同字母的指数都相同.
像3ab2与-4ab2 这样，所含字母相同，并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.
填空: (1) 100t-252t =( )t；(2) 3x2+2x2 =( )x2；(3) 3ab2-4ab2 =( )ab2．
辨别同类项要把准“两相同，两无关”.
例如，2a2b3与-3b3a2是同类项；
②相同字母的指数相同.
②与字母的排列顺序无关.
2a2b3与-3a3b2不是同类项.
1.判断下列各组中的两项是否是同类项：(1) -5ab3与3a3b ( ) (2)3xy与3x( )(3) -5m2n3与2n3m2( ) (4)53与35 ( )(5) x3与53 ( ) (6)a+b与4(a+b) ( )
判断同类项：1.字母_____；2.相同字母的指数也_____,与______无关，与_________无关.
2.若式子3a3b4-5n与-6a6-(m+1)bn-2是同类项，求m2-5mn的值.
解：因为3a3b5n-4与-6a6-(m+1)b2-n是同类项，所以3=6-(m+1)，5n-4=2-n，解得m=2，n=1，所以m2-5mn=22-5×2×1=-6.
利用有理数的运算律合并下列多项式中的同类项.
4x2+2x+7+3x-8x2-2
=4x2 -8x2 +2x+3x+7-2
= (4x2 -8x2 ) +(2x+3x)+(7-2)
= (4-8)x2+(2+3)x+(7-2)
同类项移动位置时，前面的符号不要遗漏
把一个多项式的各项按某个字母的指数从大(小)到小(大)的顺序排列起来，叫做把这个多项式按这个字母的降幂(升幂)排列.
观察：最终结果所得项中的系数、字母以及字母的指数与合并前各同类项的系数、字母及字母的指数有什么联系？
把多项式中的同类项合并成一项，叫做合并同类项.
合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变。
合并下列各式的同类项：
(1) xy2- xy2;(2) -3x2y+2x2y+3xy2-2xy2;(3) 4a2+3b2+2ab-4a2-4b2.
(1) 原式=(1- ) xy2 = xy2;
(2) 原式=(-3+2) x2y+(3-2) xy2 =-x2y+xy2 ;
(3) 原式=(4a2 -4a2 )+(3b2 -4b2)+2ab =(4-4) a2 +(3-4)b2+2ab=-b2+2ab.
两个同类项的系数互为相反数，则两项的和等于零
(1) 求多项式 2x2-5x+x2+4x-3x2-2 的值，其中x= ;
(2) 求多项式3a+abc-c2-3a+c2 的值，其中a=- ,b=2,c=-3.
原式=(2+1-3)x2+(-5+4)x-2=-x-2. 当x= 时，原式=- -2=-
(2) 原式=(3-3)a+abc+(-+ )c2=abc.当a=- ,b=2,c=-3时，原式=(- )×2×(-3)=1.
(1)水库中水位第一天连续下降了a小时，每小时平均下降 2cm；第二天连续上升了a小时，每小时平均上升0.5cm，这两天水位总的变化情况如何？
解：(1)把下降的水位变化量记为负，上升的水位变化量量记为正，第一天水位的变化量为-2a cm ，第二天水位的变化量为0.5a cm.
两天水位的总变化量(单位：cm)为
这两天水位总的变化情况为下降了1.5a cm.
-2a+0.5a=(-2+0.5)a=-1.5a(cm)
(2)某商店原有5袋大米，每袋大米为x千克，上午卖出3袋，下午又购进同样包装的大米4袋，进货后这个商店有大米多少千克？
解: (2) 把进货的数量记为正，售出的数量记为负，进货后共有大米(单位：kg)为
5x-3x+4x=(5-3+4)x=6x.
进货后这个商店共有大米6x千克.