广西区2021中考数学函数应用专题（有答案）

这是一份广西区2021中考数学函数应用专题（有答案），共15页。PPT课件主要包含了类型一文字型，x＋10，－324a，类型二表格型，x＋5y＝700，90－a，－a≤2a，≤a≤50，类型三函数图象型，例3题图等内容，欢迎下载使用。

例1 (2019北部湾经济区黑白卷)“大吉大荔大灵山，好山好水好风光”，广西是中国荔枝之乡．一水果店主分两批购进桂味荔枝，①第一批所用资金为2400元，②第二批所用资金是2700元，③第二批单价比第一批单价每箱多10元，④购进的数量比第一批少25%．(1)求该水果店主购进第一批荔枝的单价是多少元？(2)⑤已知荔枝每箱10千克，该水果店主计划两批荔枝的售价均定为每千克4元，实际销售时按计划无损耗售完第一批后，发现第二批荔枝品质不如第一批，⑥于是该店主将售价下降a%销售，结果还是出现了10%的损耗，⑦但这两批荔枝销售完后仍获利不低于2292元，求a的最大值.
【分层分析】(1)设该水果店主购进第一批荔枝的单价是x元．由题干③得第二批荔枝的单价为每箱________元．由题干①可知第一批购进的数量为________箱；由题干②可知第二批购进的数量为________箱；再由题干④列方程为______________________；(2)由(1)中购进第一批荔枝的单价可知第一批的数量为________箱；可求得购进第二批荔枝的数量为________箱；由题干⑤可知无损耗销售完第一批的利润为______元；由题干⑥知销售完第二批的利润为____________元．再根据题干⑦可列不等式为____________________________(利润＝售价－成本)．【自主作答】
2400＋540－32.4a≥2292
解：(1)设该水果店主购进第一批荔枝的单价为每箱x元，则购进第二批荔枝的单价为每箱(x＋10)元．由题意得 (1－25%)＝ ，解得x＝20，经检验，x＝20是原分式方程的解，且符合题意．答：该水果店主购进第一批荔枝的单价是每箱20元；(2)购进第一批荔枝的数量为2400÷20＝120(箱)，购进第二批荔枝的数量为120×(1－25%)＝90(箱)，由题意得4×10×120＋4×90×10×(1－10%)×(1－a%)－2400－2700≥2292，整理得648－32.4a≥0，解得a≤20.答：a的最大值为20.
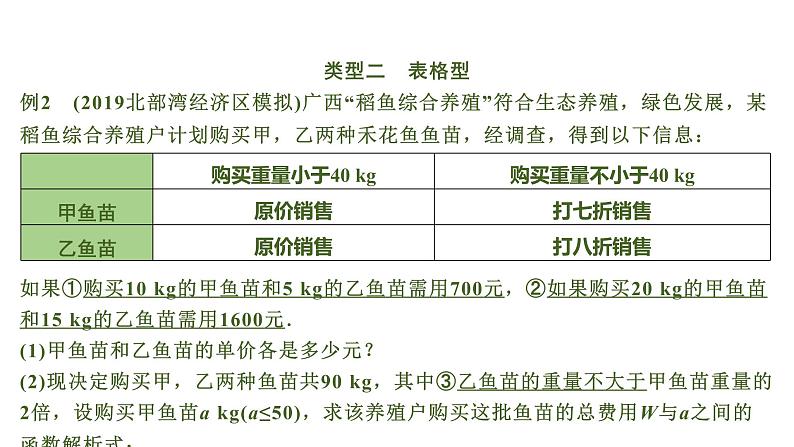
例2　(2019北部湾经济区模拟)广西“稻鱼综合养殖”符合生态养殖，绿色发展，某稻鱼综合养殖户计划购买甲，乙两种禾花鱼鱼苗，经调查，得到以下信息：
如果①购买10 kg的甲鱼苗和5 kg的乙鱼苗需用700元，②如果购买20 kg的甲鱼苗和15 kg的乙鱼苗需用1600元．(1)甲鱼苗和乙鱼苗的单价各是多少元？(2)现决定购买甲，乙两种鱼苗共90 kg，其中③乙鱼苗的重量不大于甲鱼苗重量的2倍，设购买甲鱼苗a kg(a≤50)，求该养殖户购买这批鱼苗的总费用W与a之间的函数解析式；
(3)在(2)的条件下，请设计一种购买方案，使所需总费用最低，并求出最低总费用．【分层分析】(1)由表格可知，当购买甲、乙鱼苗都不小于40 kg时才会进行打折销售，设甲、乙鱼苗的单价分别为x 元/kg，y 元/kg，故购买10 kg的甲鱼苗需用__________元，购买5千克的乙鱼苗需用__________元，由题干①可得等量关系式为_______________，同理由题干②可得等量关系式为________________；(2)由购买甲鱼苗a kg(a≤50)，购买甲、乙两种鱼苗共90 kg，则购买乙鱼苗________kg，由题干③，可列不等式______________，从而得a的取值范围为__________．再将a的取值与40进行比较，分别判断购买甲、乙鱼苗是否需要打折，最后根据总费用＝购买甲鱼苗的费用＋购买乙鱼苗的费用列出函数解析式为___________________________；
20x＋15y＝1600
(3)要求最低总费用，在(2)的情况下，判断函数解析式的增减性，再结合a的取值范围，即可得到最低总费用．【自主作答】
解：(1)设甲鱼苗价格为x元/kg，乙鱼苗价格为y元/kg，答：甲鱼苗价格为50元/kg，乙鱼苗价格为40元/kg.
(2)根据题意得90－a≤2a，解得a≥30，∵a≤50，∴30≤a≤50.①当30≤a<40时，W关于a的解析式为：W＝50a＋40×0.8×(90－a)＝18a＋2880；②当40≤a≤50时，W关于a的解析式为：W＝50×0.7a＋40×0.8×(90－a)＝3a＋2880.综上所述，W＝
(3)①当30≤a<40时，W＝18a＋2880，∵18>0，∴W随a的增大而增大，∴当a＝30时，W的值最小，W最小＝18a＋2880＝18×30＋2880＝3420.②当40≤a≤50时，W＝3a＋2880，∵3>0，∴W随a的增大而增大，∴当a＝40时，W的值最小，W最小＝3a＋2880＝3×40＋2880＝3000.∵3000<3420，∴当购买甲鱼苗40 kg，乙鱼苗50 kg时，所需总费用最低，最低总费用为3000元．
例3　(2019南宁十四中模拟)甲，乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2 h，并且甲车途中休息0.5 h，(甲车休息前后的速度相同)，甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示．(1)求m、a的值；(2)求甲车比乙车晚多少小时到达B地；(3)两车相距50 km时乙车行驶了多少小时．
【分层分析】(1)由图象可得甲车行驶的过程分为三段，先匀速行驶m小时，中途休息了________小时(列代数式)，最后再继续以原来的速度匀速行驶，由题干可知甲车中途休息了0.5 h，可得m＝________，由速度＝ ，结合图象可得甲车休息前的速度为______km/h，休息后的速度为________km/h，由休息前后的速度相等，可列等量关系式为__________；
(2)由图象可得乙车行驶的路程与时间的函数关系式为____________；甲车在1.5小时后行驶的路程与时间的函数关系式为____________．分别求出两车到达B地时所用的时间，得甲车比乙车晚________h到达B地；(3)由图象可知，在甲车行驶________h后两车相遇．故要求两车相距50 km乙车行驶了多少小时，需分________和________两种情况．分别求出甲车休息后和乙车行驶的路程与时间的函数解析式，列等量关系式_________________________________和_____________________________分别求解即可．
40x－20－(80x－160)＝50
80x－160－(40x－20)＝50
解：(1)m＝1.5－0.5＝1，由甲车休息前后速度相等，得 ＝a，解得a＝40.(2)设乙车行驶的路程与乙车行驶的时间的函数解析式为y乙＝kx＋b，将点(2，0)，(3.5，120)分别代入函数解析式，∴y乙＝80x－160，令y＝260，得80x－160＝260，解得x＝ ，
∴乙车在甲车出发 小时后到达B地．∴甲车休息后的速度为40 km/h，∴设甲车休息后行驶的路程与时间的函数解析式为y甲＝40x＋t，将(3.5，120)代入，得40×3.5＋t＝120，解得t＝－20，∴y甲＝40x－20，令y＝260，得40x－20＝260，解得x＝7，∴甲车在出发7小时后到达B地，7－ h，∴甲车比乙车晚 h到达B地．