2021年江苏省徐州市邳州市中考数学第二次质检试卷（word版，含解析）

这是一份2021年江苏省徐州市邳州市中考数学第二次质检试卷（word版，含解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）﹣3的相反数是（ ）
A．3B．﹣3C．D．﹣
2．（3分）国家统计局12月18日发布公告，经初步统计，2020年全国棉花播种面积约为3170000公顷．将3170000用科学记数法表示为（ ）
A．3.17×105B．3.17×106C．0.317×107D．31.7×106
3．（3分）下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．等边三角形B．平行四边形C．矩形D．正五边形
4．（3分）下列计算正确的是（ ）
A．a2+a2＝a4B．（a﹣b）2＝a2﹣b2
C．a2•a3＝a6D．（a2）2＝a4
5．（3分）将二次函数y＝（x+1）2﹣3的图象向上平移2个单位后得到的新抛物线的表达式为（ ）
A．y＝（x+3）2﹣3B．y＝（x﹣1）2﹣3C．y＝（x+1）2﹣5D．y＝（x+1）2﹣1
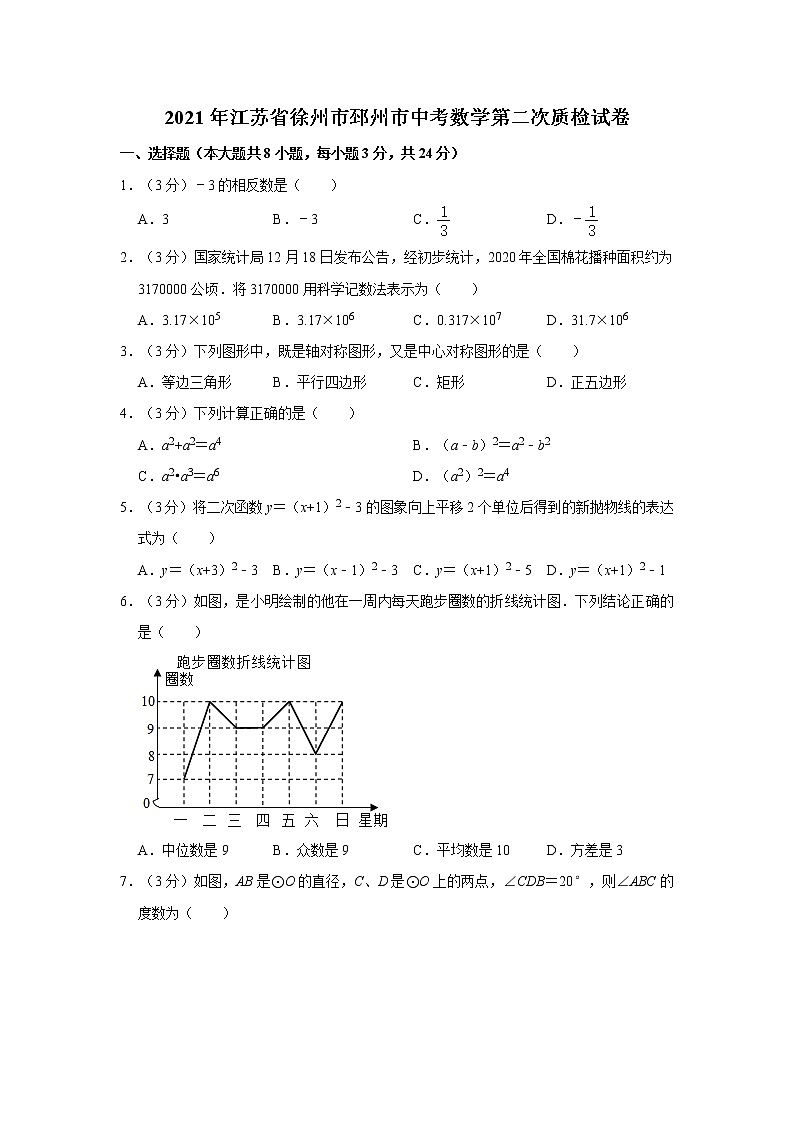
6．（3分）如图，是小明绘制的他在一周内每天跑步圈数的折线统计图．下列结论正确的是（ ）
A．中位数是9B．众数是9C．平均数是10D．方差是3
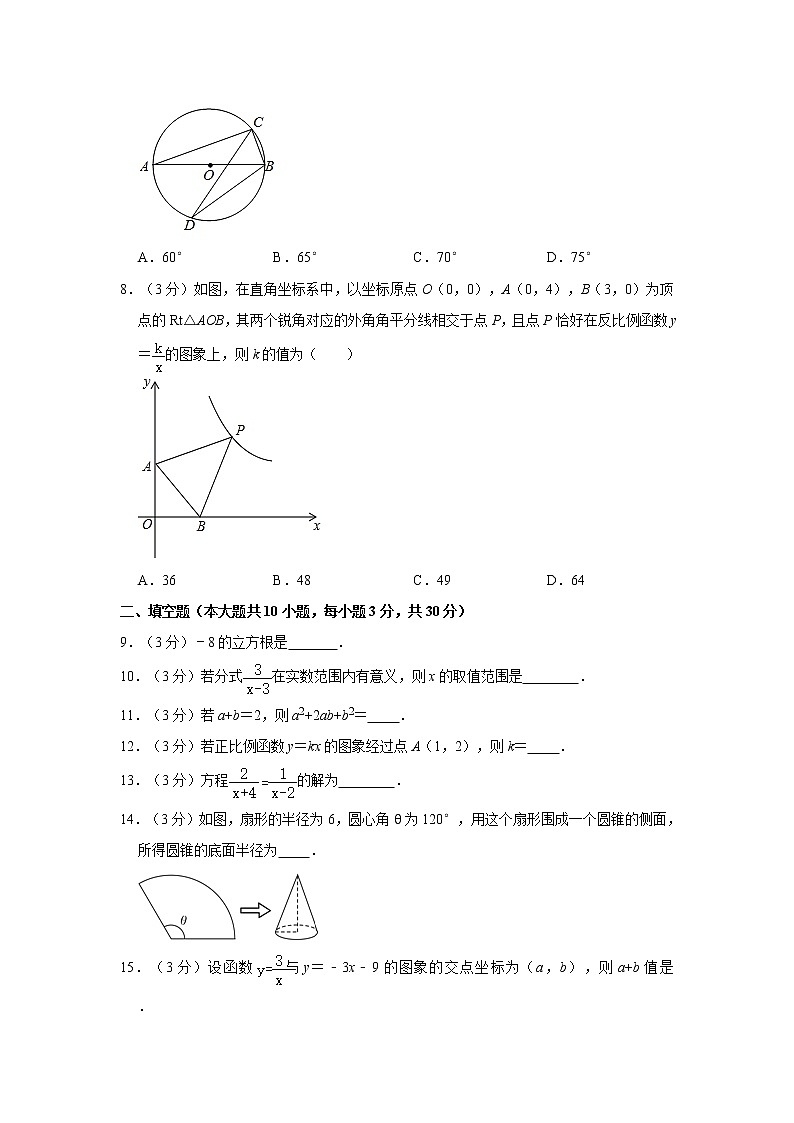
7．（3分）如图，AB是⊙O的直径，C、D是⊙O上的两点，∠CDB＝20°，则∠ABC的度数为（ ）
A．60°B．65°C．70°D．75°
8．（3分）如图，在直角坐标系中，以坐标原点O（0，0），A（0，4），B（3，0）为顶点的Rt△AOB，其两个锐角对应的外角角平分线相交于点P，且点P恰好在反比例函数y＝的图象上，则k的值为（ ）
A．36B．48C．49D．64
二、填空题（本大题共10小题，每小题3分，共30分）
9．（3分）﹣8的立方根是 ．
10．（3分）若分式在实数范围内有意义，则x的取值范围是 ．
11．（3分）若a+b＝2，则a2+2ab+b2＝ ．
12．（3分）若正比例函数y＝kx的图象经过点A（1，2），则k＝ ．
13．（3分）方程的解为 ．
14．（3分）如图，扇形的半径为6，圆心角θ为120°，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为 ．
15．（3分）设函数与y＝﹣3x﹣9的图象的交点坐标为（a，b），则a+b值是 ．
16．（3分）如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB中点，AC＝6，BD＝8，则线段OE的长为 ．
17．（3分）如图，在△ABC中，AD是BC边上的高，csC＝，AB＝10，AC＝6，则BC的长为 ．
18．（3分）如图，在平面直角坐标系中，直线l为正比例函数y＝x的图象，点A1，的坐标为（1，0），过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x轴的垂线，垂足为A3，交直线l于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形A2021B2021C2021D2021的面积是 ．
三、解答题（本大题共有10小题，共86分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（10分）计算：
（1）|﹣3|+（）﹣1+20210；
（2）÷（1﹣）．
20．（10分）（1）解方程：x2﹣4x﹣5＝0；
（2）解不等式组：．
21．（7分）为发展学生的核心素养，培养学生的综合能力，某学校计划开设四门选修课：乐器、舞蹈、绘画、书法．学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．对调查结果进行整理，绘制成两幅不完整的统计图，请结合图中所给信息解答下列问题：
（1）参与随机抽样问卷调查的有 名学生，并补全条形统计图；
（2）扇形统计图中，“乐器”所对应扇形的圆心角度数是 °；
（3）若该校有600名学生，估计选修书法的学生大约有多少名？
22．（7分）“中国结”是我国特有的手工编织工艺品，也是一种传统吉祥装饰物．如图，现有三张正面印有“中国结”图案的不透明卡片A，B，C，卡片除正面图案不同外，其余均相同．将三张卡片正面向下洗匀，小吉同学从中随机抽取一张卡片，记下图案后正面向下放回，洗匀后再从中随机抽取一张卡片，请用画树状图或列表的方法，求小吉同学抽出的两张卡片中至少有一张是B卡片的概率．
23．（8分）如图，▱ABCD的对角线AC、BD相交于点O，过点O作EF⊥AC，分别交AB、DC于点E、F，连接AF、CE．
（1）若OE＝2，求EF的长；
（2）判断四边形AECF的形状，并说明理由．
24．（8分）某停车场的收费标准如下：中型汽车的停车费为12元/辆，小型汽车的停车费为7元/辆．现在停车场内停有28辆中、小型汽车，这些车共缴纳停车费246元，求中小型汽车各有多少辆？
25．（8分）如图，⊙O为锐角△ABC的外接圆，半径为5．
（1）用尺规作图作出∠BAC的平分线，并标出它与劣弧的交点E（保留作图痕迹，不写作法）；
（2）若（1）中的点E到弦BC的距离为3，求弦CE的长．
26．（8分）某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数关系，其部分对应数据如下表所示：
（1）求y与x之间的函数表达式；
（2）该超市要想获得1280元的日销售利润，每千克樱桃的售价应定为多少元？
（3）当每千克樱桃的售价定为 元时，日销售利润最大，最大利润是 元．
27．（10分）在矩形ABCD中，AB＝1，BC＝a，点E是边BC上一动点，连接AE，将△ABE沿AE翻折，点B的对应点为点B'．
（1）如图，设BE＝x，BC＝，在点E从B点运动到C点的过程中．
①AB'+CB'最小值是 ，此时x＝ ；
②点B'的运动路径长为 ．
（2）如图，设BE＝a，当点B的对应点B'落在矩形ABCD的边上时，求a的值．
28．（10分）如图，二次函数y＝x2+bx+c的图象与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．
（1）求二次函数的表达式；
（2）若点D为抛物线对称轴上一动点，当△BCD是直角三角形时，请直接写出点D的坐标；
（3）若点E（m，n）为抛物线上的一个动点，将点E绕原点O旋转180°得到点F．
①当点F落在该抛物线上时，求m的值；
②当点F落在第二象限内且AF取得最小值时，求m的值．
2021年江苏省徐州市邳州市中考数学第二次质检试卷
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共24分）
1．（3分）﹣3的相反数是（ ）
A．3B．﹣3C．D．﹣
【分析】根据相反数的意义，只有符号不同的两个数为相反数．
【解答】解：﹣3的相反数是3．
故选：A．
2．（3分）国家统计局12月18日发布公告，经初步统计，2020年全国棉花播种面积约为3170000公顷．将3170000用科学记数法表示为（ ）
A．3.17×105B．3.17×106C．0.317×107D．31.7×106
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：3170000＝3.17×106．
故选：B．
3．（3分）下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．等边三角形B．平行四边形C．矩形D．正五边形
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：A、等边三角形是轴对称图形，不是中心对称图形．故本选项不合题意；
B、平行四边形是中心对称图形，不是轴对称图形．故本选项不合题意；
C、矩形既是轴对称图形，又是中心对称图形．故本选项符合题意；
D、正五边形是轴对称图形，不是中心对称图形．故本选项不合题意．
故选：C．
4．（3分）下列计算正确的是（ ）
A．a2+a2＝a4B．（a﹣b）2＝a2﹣b2
C．a2•a3＝a6D．（a2）2＝a4
【分析】分别根据合并同类项法则，完全平方公式，同底数幂的除法法则以及幂的乘方运算法则逐一判断即可．
【解答】解：A．a2+a2＝2a2，故本选项不合题意；
B．（a﹣b）2＝a2﹣2ab+b2，故本选项不合题意；
C．a2•a3＝a5，故本选项不合题意；
D．（a2）2＝a4，故本选项符合题意；
故选：D．
5．（3分）将二次函数y＝（x+1）2﹣3的图象向上平移2个单位后得到的新抛物线的表达式为（ ）
A．y＝（x+3）2﹣3B．y＝（x﹣1）2﹣3C．y＝（x+1）2﹣5D．y＝（x+1）2﹣1
【分析】先根据二次函数的性质得到抛物线y＝（x+1）2﹣3的顶点坐标为（﹣1，﹣3），再利用点平移的规律，点（﹣1，﹣3）平移后的对应点的坐标为（﹣1，﹣1），然后根据顶点式写出平移后的抛物线解析式．
【解答】解：抛物线y＝﹣（x+1）2﹣3的顶点坐标为（﹣1，﹣3），把点（﹣1，﹣3）向上平移2个单位得到对应点的坐标为（﹣1，﹣1），
所以平移后的抛物线解析式为y＝（x+1）2﹣1，
故选：D．
6．（3分）如图，是小明绘制的他在一周内每天跑步圈数的折线统计图．下列结论正确的是（ ）
A．中位数是9B．众数是9C．平均数是10D．方差是3
【分析】由折线图得到一周内每天跑步圈数的数据，计算这组数据的平均数、中位数、众数、方差，然后判断得结论．
【解答】解：A．排序后的数据中，最中间的数据为9，即中位数为9，故本选项正确，符合题意；
B．数据10出现的次数最多，即众数是10，故本选项错误，不符合题意；
C．平均数为：（7+8+9+9+10+10+10）＝9，故本选项错误，不符合题意；
D．方差为[（7﹣9）2+（8﹣9）2+（9﹣9）2+（9﹣9）2+（10﹣9）2+（10﹣9）2+（10﹣9）2]＝，故本选项错误，不符合题意；
故选：A．
7．（3分）如图，AB是⊙O的直径，C、D是⊙O上的两点，∠CDB＝20°，则∠ABC的度数为（ ）
A．60°B．65°C．70°D．75°
【分析】利用圆周角定理证明∠ACB＝90°，再利用圆周角定理求出∠CAB可得结论．
【解答】解：∵AB是直径，
∴∠ACB＝90°，
∵∠CAB＝∠CDB＝20°，
∴∠ABC＝90°﹣20°＝70°，
故选：C．
8．（3分）如图，在直角坐标系中，以坐标原点O（0，0），A（0，4），B（3，0）为顶点的Rt△AOB，其两个锐角对应的外角角平分线相交于点P，且点P恰好在反比例函数y＝的图象上，则k的值为（ ）
A．36B．48C．49D．64
【分析】过P分别作AB、x轴、y轴的垂线，垂足分别为C、D、E，如图，利用勾股定理计算出AB＝5，根据角平分线的性质得PE＝PC＝PD，设P（t，t），利用面积的和差得到×t×（t﹣4）+×5×t+×t×（t﹣3）+×3×4＝t×t，求出t得到P点坐标，然后把P点坐标代入y＝中求出k的值．
【解答】解：过P分别作AB、x轴、y轴的垂线，垂足分别为C、D、E，如图，
∵A（0，4），B（3，0），
∴OA＝4，OB＝3，
∴AB＝＝5，
∵△OAB的两个锐角对应的外角角平分线相交于点P，
∴PE＝PC，PD＝PC，
∴PE＝PC＝PD，
设P（t，t），则PC＝t，
∵S△PAE+S△PAB+S△PBD+S△OAB＝S矩形PEOD，
∴×t×（t﹣4）+×5×t+×t×（t﹣3）+×3×4＝t×t，
解得t＝6，
∴P（6，6），
把P（6，6）代入y＝得k＝6×6＝36．
故选：A．
二、填空题（本大题共10小题，每小题3分，共30分）
9．（3分）﹣8的立方根是 ﹣2 ．
【分析】利用立方根的定义即可求解．
【解答】解：∵（﹣2）3＝﹣8，
∴﹣8的立方根是﹣2．
故答案为：﹣2．
10．（3分）若分式在实数范围内有意义，则x的取值范围是 x≠3 ．
【分析】根据分式意义的条件即可求出答案．
【解答】解：x﹣3≠0，
∴x≠3
故答案为：x≠3
11．（3分）若a+b＝2，则a2+2ab+b2＝ 4 ．
【分析】根据完全平方公式求解即可．
【解答】解：∵a+b＝2，
∴a2+2ab+b2＝（a+b）2＝22＝4，
故答案为：4．
12．（3分）若正比例函数y＝kx的图象经过点A（1，2），则k＝ 2 ．
【分析】把A点的坐标代入函数解析式y＝kx，再求出k即可．
【解答】解：∵正比例函数y＝kx的图象经过点A（1，2），
∴2＝k×1，
解得：k＝2，
故答案为：2．
13．（3分）方程的解为 x＝8 ．
【分析】方程两边都乘以（x+4）（x﹣2），将分式方程转化为整式方程，解整式方程，最后检验即可．
【解答】解：方程两边都乘以（x+4）（x﹣2）得：2（x﹣2）＝x+4，
解得：x＝8，
检验：当x＝8时，（x+4）（x﹣2）≠0，
∴x＝8是原方程的根．
故答案为：x＝8．
14．（3分）如图，扇形的半径为6，圆心角θ为120°，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为 2 ．
【分析】易得扇形的弧长，除以2π即为圆锥的底面半径．
【解答】解：扇形的弧长＝＝4π，
∴圆锥的底面半径为4π÷2π＝2．
故答案为：2．
15．（3分）设函数与y＝﹣3x﹣9的图象的交点坐标为（a，b），则a+b值是 ﹣6﹣或﹣6+ ．
【分析】把点的坐标代入函数的解析式可得到ab＝3，b＝﹣3a﹣9，然后求得a、b的值即可求得答案．
【解答】解：∵函数与y＝﹣3x﹣9的图象的交点坐标为（a，b），
∴ab＝3，b＝﹣3a﹣9，
a（﹣3a﹣9）＝3，
整理得，a2+3a+1＝0，
解得a＝或x＝
∴b＝或b＝，
∴a+b＝﹣6﹣或﹣6+
故答案为：﹣6﹣或﹣6+．
16．（3分）如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB中点，AC＝6，BD＝8，则线段OE的长为 ．
【分析】由菱形的性质可得OA＝OC＝3，OB＝OD＝4，AO⊥BO，由勾股定理求出AB，再由直角三角形斜边上的中线性质即可得出结果．
【解答】解：∵四边形ABCD是菱形，AC＝6，BD＝8，
∴OA＝OC＝3，OB＝OD＝4，AO⊥BO，
在Rt△AOB中，由勾股定理得：AB＝＝＝5，
∵E为AB中点，
∴OE＝AB＝
故答案为：．
17．（3分）如图，在△ABC中，AD是BC边上的高，csC＝，AB＝10，AC＝6，则BC的长为 3+ ．
【分析】在Rt△ACD中，利用csC＝，可求CD，利用勾股定理求得AD，在Rt△ADB中，利用勾股定理求得BD，则BC＝CD+BD，结论可得．
【解答】解：∵AD是BC边上的高，
∴∠ADC＝90°．
∵csC＝，
∴．
∴CD＝AC＝×6＝3．
∴AD＝．
在Rt△ADB中，
BD＝．
∴BC＝CD+BD＝3+．
故答案为：3+．
18．（3分）如图，在平面直角坐标系中，直线l为正比例函数y＝x的图象，点A1，的坐标为（1，0），过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x轴的垂线，垂足为A3，交直线l于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形A2021B2021C2021D2021的面积是 ．
【分析】根据正比例函数的性质得到∠D1OA1＝45°，分别求出正方形A1B1C1D1的面积、正方形A2B2C2D2的面积，总结规律解答．
【解答】解：∵直线l为正比例函数y＝x的图象，
∴∠D1OA1＝45°，
∴D1A1＝OA1＝1，
∴正方形A1B1C1D1的面积＝1＝（）1﹣1，
由勾股定理得，OD1＝，D1A2＝，
∴A2B2＝A2O＝，
∴正方形A2B2C2D2的面积＝（）2﹣1，
同理，A3D3＝OA3＝，
∴正方形A3B3C3D3的面积＝＝（）3﹣1，
…
由规律可知，正方形AnBn∁nDn的面积＝（）n﹣1，
∴正方形A2021B2021C2021D2021的面积＝（）2020，
故答案为：（）2020．
三、解答题（本大题共有10小题，共86分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（10分）计算：
（1）|﹣3|+（）﹣1+20210；
（2）÷（1﹣）．
【分析】（1）先计算绝对值、负整数指数幂、零指数幂，再计算加法即可；
（2）先将被除式分子、分母因式分解，同时计算括号内分式的减法，再将除法转化为乘法，继而约分即可．
【解答】解：（1）原式＝3+2+1＝6；
（2）原式＝÷（﹣）
＝÷
＝•
＝．
20．（10分）（1）解方程：x2﹣4x﹣5＝0；
（2）解不等式组：．
【分析】（1）将方程左边因式分解得：（x﹣5）（x+1）＝0，得两个一元一次方程：x﹣5＝0或x+1＝0，即可求解；
（2）先求出每个不等式的解集，再取其公共部分即可求解．
【解答】解：（1）原方程可变形为：（x﹣5）（x+1）＝0，
∴x﹣5＝0或x+1＝0，
解得x1＝5，x2＝﹣1；
（2）解不等式2x﹣1＜3得x＜2，
解不等式4x+6≥x﹣3得x≥﹣3，
所以不等式组的解集为﹣3≤x＜2．
21．（7分）为发展学生的核心素养，培养学生的综合能力，某学校计划开设四门选修课：乐器、舞蹈、绘画、书法．学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．对调查结果进行整理，绘制成两幅不完整的统计图，请结合图中所给信息解答下列问题：
（1）参与随机抽样问卷调查的有 50 名学生，并补全条形统计图；
（2）扇形统计图中，“乐器”所对应扇形的圆心角度数是 108 °；
（3）若该校有600名学生，估计选修书法的学生大约有多少名？
【分析】（1）“舞蹈”的频数是10人，频率为20%，可求出调查人数，进而求出“绘画”“书法”的频数，补全条形统计图；
（2）求出“乐器”所占得百分比，即可求出相应扇形的圆心角度数；
（3）求出“书法”所占得百分比即可求出答案．
【解答】解：（1）调查人数为：10÷20%＝50（名），
绘画人数为：50×40%＝20（名），
书法人数为：50﹣10﹣15﹣20＝5（名），补全条形统计图，如图所示：
故答案为：50；
（2）360°×＝108°，
故答案为：108；
（3）（名），
答：估计选修书法的学生大约有60名．
22．（7分）“中国结”是我国特有的手工编织工艺品，也是一种传统吉祥装饰物．如图，现有三张正面印有“中国结”图案的不透明卡片A，B，C，卡片除正面图案不同外，其余均相同．将三张卡片正面向下洗匀，小吉同学从中随机抽取一张卡片，记下图案后正面向下放回，洗匀后再从中随机抽取一张卡片，请用画树状图或列表的方法，求小吉同学抽出的两张卡片中至少有一张是B卡片的概率．
【分析】画树状图，共有9种等可能的结果，其中至少有一张是B卡片的情况有5种，再由概率公式求解即可．
【解答】解：画树状图如图：
共有9种等可能的结果，其中至少有一张是B卡片的情况有5种，
∴小吉同学抽出的两张卡片中至少有一张是B卡片的概率为．
23．（8分）如图，▱ABCD的对角线AC、BD相交于点O，过点O作EF⊥AC，分别交AB、DC于点E、F，连接AF、CE．
（1）若OE＝2，求EF的长；
（2）判断四边形AECF的形状，并说明理由．
【分析】（1）判定△DOF≌△BOE（ASA），即可得OE＝OF＝2，进而得出EF的长；
（2）先判定四边形AECF是平行四边形，再根据EF⊥AC，即可得到四边形AECF是菱形．
【解答】解：（1）∵四边形ABCD为平行四边形，
∴AB∥CD，OD＝OB，
∵AB∥CD，
∴∠DFO＝∠BEO，∠FDO＝∠EBO．
∴△DOF≌△BOE（ASA），
∴OE＝OF，
∵OE＝2，
∴EF＝4；
（2）四边形AECF是菱形，
理由：∵OE＝OF，OD＝OB，
∴四边形AECF是平行四边形，
∵EF⊥AC，
∴平行四边形AECF是菱形．
24．（8分）某停车场的收费标准如下：中型汽车的停车费为12元/辆，小型汽车的停车费为7元/辆．现在停车场内停有28辆中、小型汽车，这些车共缴纳停车费246元，求中小型汽车各有多少辆？
【分析】设中型汽车有x辆，小型汽车有y辆，根据“停车场内停有28辆中、小型汽车，且这些车共缴纳停车费246元”，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【解答】解：设中型汽车有x辆，小型汽车有y辆，
依题意得：，
解得：．
答：中型汽车有10辆，小型汽车有18辆．
25．（8分）如图，⊙O为锐角△ABC的外接圆，半径为5．
（1）用尺规作图作出∠BAC的平分线，并标出它与劣弧的交点E（保留作图痕迹，不写作法）；
（2）若（1）中的点E到弦BC的距离为3，求弦CE的长．
【分析】（1）利用基本作图作AE平分∠BAC；
（2）连接OE交BC于F，连接OC，如图，根据圆周角定理得到＝，再根据垂径定理得到OE⊥BC，则EF＝3，OF＝2，然后在Rt△OCF中利用勾股定理计算出CF＝，在Rt△CEF中利用勾股定理可计算出CE．
【解答】解：（1）如图，AE为所作；
（2）连接OE交BC于F，连接OC，如图，
∵AE平分∠BAC，
∴∠BAE＝∠CAE，
∴＝，
∴OE⊥BC，
∴EF＝3，
∴OF＝5﹣3＝2，
在Rt△OCF中，CF＝＝，
在Rt△CEF中，CE＝＝．
26．（8分）某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数关系，其部分对应数据如下表所示：
（1）求y与x之间的函数表达式；
（2）该超市要想获得1280元的日销售利润，每千克樱桃的售价应定为多少元？
（3）当每千克樱桃的售价定为 40 元时，日销售利润最大，最大利润是 1440 元．
【分析】（1）利用待定系数法求解即可；
（2）根据日利润＝每千克的利润×日销售量列出关于x的方程，解之求出x的值，结合x的取值范围可得答案；
（3）设日销售利润为W，根据以上相等关系列出关于x的函数解析式，配方成顶点式，利用二次函数的性质求解即可．
【解答】解：（1）设y＝kx+b，
由题意得：
解得：
所以y与x之间的函数表达式为y＝﹣2x+152．
（2）根据题意得：（x﹣20）（﹣2x+152）＝1280，
解得：x1＝60，x2＝36，
∵20≤x≤40，
∴x1＝60（不合题意，应舍去），
∴x＝36，
答：每千克樱桃的售价应定为36元．
（3）设日销售利润为W，
则W＝（x﹣20）（﹣2x+152）
＝﹣2x2+192x﹣3040
＝﹣2（x﹣48）2+1568，
∵﹣2＜0，
∴当x＜48时，W随x的增大而增大，
又20≤x≤40，
∴当x＝40时，W取得最大值，最大值为1440，
即当每千克樱桃的售价定为40元时，日销售利润最大，最大利润是1440元，
故答案为：40，1440．
27．（10分）在矩形ABCD中，AB＝1，BC＝a，点E是边BC上一动点，连接AE，将△ABE沿AE翻折，点B的对应点为点B'．
（1）如图，设BE＝x，BC＝，在点E从B点运动到C点的过程中．
①AB'+CB'最小值是 2 ，此时x＝ ；
②点B'的运动路径长为 ．
（2）如图，设BE＝a，当点B的对应点B'落在矩形ABCD的边上时，求a的值．
【分析】（1）①由折叠的性质得AB'＝AB＝1，∠AB'E＝∠B，当A、B'、C三点共线时，AB'+CB'的值最小＝AC＝2，则AB＝AC，B'C＝AC﹣AB'＝1，再证∠ACB＝30°，AB'＝B'C，即可解决问题；
②先证点B'在以A为圆心，1为半径的圆上，再求出∠BAB'＝2∠BAC＝120°，然后由弧长公式求解即可；
（2）分两种情况，①当点B'落在AD边上时，则四边形ABEB'为正方形，得BE＝AB＝1，即可求解；
②当点B'落在CD边上时，证△CEB'∽△DB'A，得，即可求解．
【解答】解：（1）①连接B'C，如图1所示：
由折叠的性质得：AB'＝AB＝1，∠AB'E＝∠B，
∵四边形ABCD是矩形，
∴∠AB'E＝∠B＝90°，
∴EB'⊥AB'，
当A、B'、C三点共线时，如图1所示：
AB'+CB'的值最小＝AC＝＝＝2，
则AB＝AC，B'C＝AC﹣AB'＝1，
∴∠ACB＝30°，AB'＝B'C，
∴∠BAC＝90°﹣30°＝60°，AE＝CE，
∴∠EAC＝∠ACB＝30°，
∴∠BAE＝30°，
∴BE＝AB＝，
故答案为：2，；
②∵在点E从B点运动到C点的过程中始终有AB'＝1，
∴点B'在以A为圆心，1为半径的圆上，
由（1）得：∠BAC＝60°，
∴∠BAB'＝2∠BAC＝120°，
∴点B'的运动路径长为＝π，
故答案为：；
（2）分两种情况：
①当点B'落在AD边上时，如图3所示：
则四边形ABEB'为正方形，
∴BE＝AB＝1，
∴，
解得：；
②当点B'落在CD边上时，如图4所示：
∵四边形ABCD是矩形，
∴AD＝BC＝a，∠B＝∠C＝∠D＝90°，
由折叠的性质得：B'E＝BE＝a，AB＝AB'＝1，∠AB'E＝∠B＝90°，
∵BC＝a，
∴CE＝BC﹣BE＝a，
在Rt△AB'D中，由勾股定理得：B'D＝＝＝，
∵∠B'EC+∠EB'C＝∠EB'C+∠AB'D＝90°，
∴∠B'EC＝∠AB'D，
∴△CEB'∽△DB'A，
∴，
即，
解得：，
∵a＞0，
∴；
综上所述，当点B的对应点B'落在矩形ABCD的边上时，或．
28．（10分）如图，二次函数y＝x2+bx+c的图象与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．
（1）求二次函数的表达式；
（2）若点D为抛物线对称轴上一动点，当△BCD是直角三角形时，请直接写出点D的坐标；
（3）若点E（m，n）为抛物线上的一个动点，将点E绕原点O旋转180°得到点F．
①当点F落在该抛物线上时，求m的值；
②当点F落在第二象限内且AF取得最小值时，求m的值．
【分析】（1）A（﹣1，0）、B（3，0）代入y＝x2+bx+c解得b、c，即可得答案；
（2）设D（1，t），用含t的代数式表示△BCD的三边，分三种情况：①∠BCD＝90°，②∠DBC＝90°，③∠BDC＝90°，用勾股定理逆定理列方程，解出t即可得答案；
（3）①将E（m，n）代入y＝x2﹣2x﹣3得n＝m2﹣2m﹣3，将F（﹣m，﹣n）代入y＝x2﹣2x﹣3得﹣n＝m2+2m﹣3，即n＝﹣m2﹣2m+3，即可解得m＝±；
②由F（﹣m，﹣n）在第二象限得m＞0，n＜0，又抛物线y＝x2﹣2x﹣3的顶点坐标为（1，﹣4），可得﹣4≤n＜0，E（m，n）在抛物线y＝x2﹣2x﹣3上，可得m2﹣2m＝n+3，AF2＝（﹣m+1）2+（﹣n）2＝m2﹣2m+1+n2＝n+3+1+n2＝n2+n+4＝（n+）2+，根据AF取最小值得n＝﹣，由m2﹣2m﹣3＝﹣即可得m的值．
【解答】解：（1）将A（﹣1，0）、B（3，0）代入y＝x2+bx+c得：
解得：，
∴二次函数表达式为y＝x2﹣2x﹣3；
（2）在y＝x2﹣2x﹣3中，令x＝0得y＝﹣3，对称轴为直线x＝＝1，
∴C（0，﹣3），
设D（1，t），而B（3，0），则BC＝＝3，DC＝＝，DB＝＝，
△BCD是直角三角形，分三种情况：
①∠BCD＝90°，如图：
此时DC2+BC2＝DB2，
∴t2+6t+10+18＝t2+4，
解得t＝﹣4，
∴D（1，﹣4）；
②∠DBC＝90°，如图：
此时BC2+DB2＝DC2，
∴18+t2+4＝t2+6t+10，
解得t＝2，
∴D（1，2）；
③∠BDC＝90°，如图：
此时DC2+DB2＝BC2，
∴t2+6t+10+t2+4＝18，
解得t＝或t＝，
∴D（1，）或（1，），
综上所述，△BCD是直角三角形，D坐标为（1，﹣4）或（1，2）或（1，）或（1，）；
（3）①∵E（m，n）在抛物线y＝x2﹣2x﹣3上，
∴n＝m2﹣2m﹣3，
∵将点E绕原点O旋转180°得到点F，即点E与F关于原点对称，
∴F（﹣m，﹣n），
由F（﹣m，﹣n）在抛物线y＝x2﹣2x﹣3上，
∴﹣n＝m2+2m﹣3，即n＝﹣m2﹣2m+3，
∴m2﹣2m﹣3＝﹣m2﹣2m+3，
解得m＝±；
②由题意可知F（﹣m，﹣n）在第二象限，
∴﹣m＜0，﹣n＞0，即m＞0，n＜0，
∵抛物线y＝x2﹣2x﹣3的顶点坐标为（1，﹣4），
∴﹣4≤n＜0，
∵E（m，n）在抛物线y＝x2﹣2x﹣3上，
∴n＝m2﹣2m﹣3，
∴m2﹣2m＝n+3，
∵A（﹣1，0），F（﹣m，﹣n），
∴AF2＝（﹣m+1）2+（﹣n）2
＝m2﹣2m+1+n2
＝n+3+1+n2
＝n2+n+4
＝（n+）2+，
∴当n＝﹣时，AF2有最小值，即AF取得最小值，
由m2﹣2m﹣3＝﹣，解得m＝或m＝，
∵m＞0，
∴m＝不合题意，应舍去，
∴m的值为．
每千克售价x（元）
…
25
30
35
…
日销售量y（千克）
…
102
92
82
…
每千克售价x（元）
…
25
30
35
…
日销售量y（千克）
…
102
92
82
…