

2021年云南省昆明市禄劝初中学业水平模拟考试(一)数学(word版 含答案)
展开2021年云南省昆明市禄劝初中学业水平模拟考试(一)数学
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果正n边形的一个外角是40°,则n的值为( )
A.5 B.6 C.8 D.9
2.若分式有意义,则实数x的取值范围是( )
A. B. C. D.
3.5G网络是实现万物互联互通的关键基础设施,数据显示,截止2020年9月底,中国5G基站累计超过690000个,将数据690000用科学记数法表示为( )
A. B. C. D.
4.如图是一个由若干个相同的小正方体组成的几何体的三种形状图,则组成这个几何体的小正体的个数是( )
A.7 B.8 C.9 D.10
5.关于的一元二次方程没有实数根,则实数的值可以为( )
A.0 B.1 C.2 D.3
6.下列运算正确的是( )
A. B.
C. D.
7.已知圆锥的底面半径为2,母线长为4,则其侧面积为( )
A. B. C. D.
8.观察“田”字中各数之间的关系:
则a+d﹣b﹣c的值为( )
A.52 B.﹣52 C.51 D.51
二、填空题
9.的倒数是______.
10.把多项式因式分解的结果是________.
11.当m__时,函数y=的图象在第二、四象限内.
12.已知一组数据的平均数等于,则这组数据的中位数等于_______.
13.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为________.
14.如图,已知函数y1=,y2=在第一象限的图象.过函数y1=的图象上的任意一点A作x轴的平行线交函数y2=的图象于点B,交y轴于点C.若△AOB的面积S=l,则k的值为
三、解答题
15.计算:.
16.先化简,再求值:,其中a在-1,1,2中选一个适合的数代入求值.
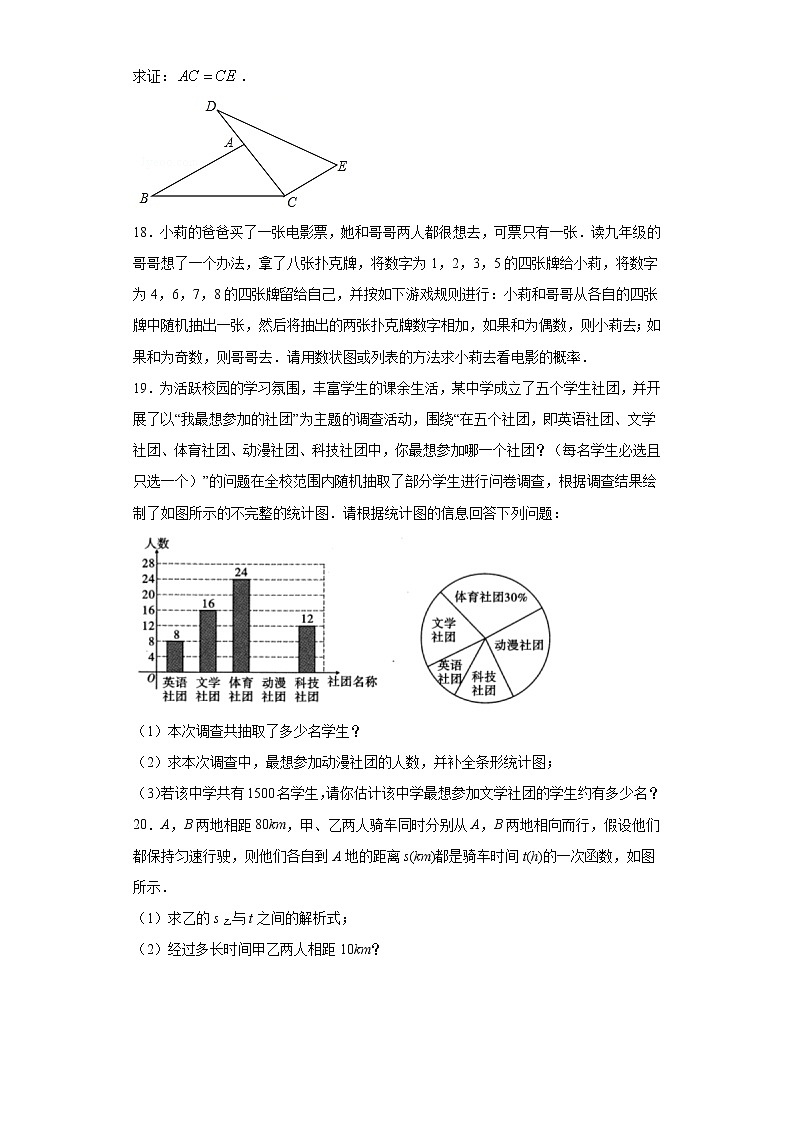
17.如图,点、、在同一直线上,,,.
求证:.
18.小莉的爸爸买了一张电影票,她和哥哥两人都很想去,可票只有一张.读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.请用数状图或列表的方法求小莉去看电影的概率.
19.为活跃校园的学习氛围,丰富学生的课余生活,某中学成立了五个学生社团,并开展了以“我最想参加的社团”为主题的调查活动,围绕“在五个社团,即英语社团、文学社团、体育社团、动漫社团、科技社团中,你最想参加哪一个社团?(每名学生必选且只选一个)”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整的统计图.请根据统计图的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)求本次调查中,最想参加动漫社团的人数,并补全条形统计图;
(3)若该中学共有1500名学生,请你估计该中学最想参加文学社团的学生约有多少名?
20.A,B两地相距80km,甲、乙两人骑车同时分别从A,B两地相向而行,假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t(h)的一次函数,如图所示.
(1)求乙的s乙与t之间的解析式;
(2)经过多长时间甲乙两人相距10km?
21.如图,是的外接圆,,点E是弧的中点,过点E作,交的延长线于点D,连接交于点F.
(1)判断与的位置关系,并证明你的结论;
(2)若,,求的长.
22.抛物线的顶点为(1,﹣4),与x轴交于A、B两点,与y轴负半轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)点P为对称轴右侧抛物线上一点,以BP为斜边作等腰直角三角形,直角顶点M落在对称轴上,求P点的坐标.
23.如图甲,已知在四边形中,,,平分,交于点E,过点E作,交于点F,O是的中点,连接,,.
(1)求证:四边形是菱形;
(2)若,如图乙所示:
①求证:;
②若,,求的长.
参考答案
1.D
【分析】
根据多边形外角和是360°即可求解.
【详解】
∵n边形的外角和为360°,
∴正n边形的一个外角是 ,
∴=40°,
∴n=9,
故选D.
2.C
【分析】
直接利用分式有意义的条件得出x的值,进而得出答案.
【详解】
解:若分式有意义,
则,
解得:,
故选:C.
【点睛】
本题主要考查了分式有意义的条件,正确把握分式有意义的条件:分式有意义的条件是分母不等于零是解题关键.
3.B
【分析】
科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【详解】
解:.
故选:B.
【点睛】
本题考查科学记数法的表示方法,熟悉相关性质是解题的关键.
4.C
【分析】
根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形进行判断.
【详解】
解:综合三视图,这个几何体的底层有3+2+1=6个小正方体,第二层有1+1=2个小正方体,第三层有1个,因此组成这个几何体的小正方形有6+2+1=9个.
故选C.
【点睛】
本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就容易得到答案了.
5.D
【分析】
利用一元二次方程根的判别式即可求出n的取值范围,即可选择.
【详解】
根据题意可知:,
∴.
∴符合题意的选项为D.
故选:D.
【点睛】
本题考查一元二次方程根的判别式和解一元一次不等式.根据题意可知一元二次方程没有实数根时其根的判别式小于0是解答本题的关键.
6.D
【分析】
根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可.
【详解】
解:A、 ,故本选项错误;
B、,故本选项错误;
C、,故本选项错误;
D、,故本选项正确;
故选:D.
【点睛】
本题考查了单项式与单项式相乘,熟练掌握运算法则是解题的关键.
7.A
【分析】
圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.
【详解】
解:圆锥的侧面积=2π×2×4÷2=8π,
故选A.
【点睛】
考查圆锥的侧面积的求法,解题的关键是熟记圆锥的侧面积的计算公式.
8.B
【分析】
根据题目中的图形,可以发小数字的变化规律,从而可以求得a、b、c、d的值,从而可以解答本题.
【详解】
解:由图可得,
左上角的数字分别为1,3,5,7,9,…,是一些连续的奇数,
左下角的数字依次是2,4,8,16,32,…,则可以用2n表示,
右下角的数字是左上角和左下角的数字之和,
右上角的数字比右下角的数字小1,
则a=11,b=26=64,d=11+64=75,c=75﹣1=74,
∴a+d﹣b﹣c=11+75﹣64﹣74=﹣52,
故选B.
【点睛】
本题考查数字的变化类,解答本题的关键是明确题意,发现题目中数字的变化规律.
9.
【分析】
先进行化简绝对值,然后再求倒数即可.
【详解】
∵,
∴的倒数是;
故答案为:.
【点睛】
本题考查了绝对值的化简,倒数的定义,解题的关键是掌握绝对值和倒数的定义进行解题.
10.
【分析】
先提取公因式a,再利用完全平方公式因式分解即可.
【详解】
解:
故答案为:
【点睛】
本题考查因式分解,分解要彻底是关键.
11.<1
【分析】
根据反比例函数的性质,结合反比例函数图象所在象限,求出m的取值范围.
【详解】
解:∵函数y=的图象在第二、四象限内,
∴m﹣1<0,
∴m<1,
故当m<1时,函数y=的图象在第二、四象限内,
故答案为:<1.
【点睛】
本题主要考查了反比例函数的性质,象限内点的坐标特征,关键是根据反比例函数图象的位置确定m的取值范围.
12.2
【分析】
首先根据平均数的定义求出x,再根据中位数定义:将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,首先把数据从小到大排列起来,再找出中间的数即可.
【详解】
解:∵-1、2、x、3、1的平均数等于1.4,
∴(-1+2+x+3+1)÷5=1.4,
解得:x=2,
将数据从小到大重新排列:-1,1,2,2,3最中间的那个数是:2,
∴中位数是:2.
故答案为:2.
【点睛】
此题主要考查了中位数定义以及平均数的求法,关键是首先求出x的值.
13.45°
【详解】
先求出∠AOE=60°,再求出∠COE=∠AOE=60°,然后由OD平分∠BOC,得出∠BOD= ∠BOC=15°,即可求出∠DOE=∠BOD+∠BOE=45°.
故答案为45°.
14.6
【详解】
根据反比例函数图形几何意义可以得出△OAC的面积为,
△OBC的面积为,
由图像可知,
可得,
解得k=6
故答案为:6
考点:1反比例函数图像上点的几何意义;2反比例函数解析式的确定.
15..
【分析】
根据负指数幂,特殊角的三角函数值,零次幂,绝对值和二次根式的性质化简,然后再计算即可.
【详解】
解:
.
【点睛】
本题主要考查解负指数幂,特殊角的三角函数值,零次幂,绝对值和二次根式的性质,熟悉相关性质是解题的关键.
16.;1.
【分析】
先根据分式的混合运算顺序和运算法则化简原式,再选择使分式有意义的x的值代入计算可得.
【详解】
解:
,
不能为-1,1,
取2,
当时,原式.
【点睛】
本题主要考查分式的混合运算,掌握分式的混合运算顺序和运算法则是解题的关键是.
17.见解析
【分析】
先根据平行线的性质得出,再根据ASA证明,即可得出结论.
【详解】
证明:∵,
∴,
在和中,
∴,
∴.
【点睛】
本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.
18.
【分析】
结合题意,根据列表法求概率,即可得到答案.
【详解】
列表如下:
和 | 1 | 2 | 3 | 5 |
4 | 5 | 6 | 7 | 9 |
6 | 7 | 8 | 9 | 11 |
7 | 8 | 9 | 10 | 12 |
8 | 9 | 10 | 11 | 13 |
∴共有16种等可能的结果,其中和为偶数的有6种,
∴小莉去看电影的概率.
【点睛】
本题考查了概率的知识;解题的关键是熟练掌握列表法求概率的性质,从而完成求解.
19.(1)80名;(2)20名;见解析;(3)300名
【分析】
(1)用体育社团人数除以其所占百分比即可;
(2)先求出最想参加动漫社团的人数,补全条形统计图即可;
(3)全校总人数乘最想参加文学社团的学生频率即可.
【详解】
解:(1)(名).
答:本次调查共抽取了80名学生.
(2)最想参加动漫社团的人数:(名),
补全条形统计图如图1所示:
(3)(名)
答:该中学最想参加文学社团的学生约有300名.
【点睛】
本题主要考查了条形统计图,扇形统计图,用样本估计总体,解题的关键是读懂图,找出对应数据,解决问题.
20.(1)s乙=﹣20t+80;(2)t=2或.
【分析】
(1)s乙与t之间的解析式为:y=kt+80,将点(1,60)代入上式并解得:k=−20,即可求解;
(2)由题意得:s甲−s乙=±10,即可求解.
【详解】
解:(1)s乙与t之间的解析式为:y=kt+80,
将点(1,60)代入上式并解得:k=﹣20,
故s乙与t之间的解析式为:y=﹣20t+80;
(2)同理s甲与t之间的解析式为:y=15t,
由题意得:s甲﹣s乙=±10,
即﹣20t+80﹣15t=±10,
解得:t=2或.
【点睛】
此题为一次函数的应用,渗透了函数与方程的思想,重点是求乙的k值.
21.(1)与相切,见解析;(2)16.
【分析】
(1)连接,由点E是弧的中点,得到,推出,根据平行线的判定定理得到,根据平行线的性质得到,于是得到结论;
(2)连接,根据圆周角定理得到,推出,解直角三角形即可得到结论.
【详解】
解:(1)与相切.
理由:如图2,连接,
,
.
点E是弧的中点,
,
,
,
.
,
,
是的切线.
(2)连接,
为的直径,
.
由(1)知,
.
又,
,
,
在中,设,,由勾股定理,得,
,
.
,
.
【点睛】
本题考查了切线的判定与性质、解直角三角形、平行线的性质、垂径定理、圆周角定理以及角平分线的性质,熟悉相关性质是解题的关键.
22.(1)y=x2﹣2x﹣3;(2)点P的坐标为(2,﹣3)或(4,5).
【分析】
(1)由抛物线的顶点坐标可设抛物线的解析式为y=a(x-1)2-4,代入点C的坐标可求出a值,进而可得出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点A,B的坐标,设抛物线对称轴与x轴交于点E,过点P作PF∥x轴,交抛物线对称轴于点F,易证△MBE≌△PMF,根据全等三角形的性质可得出ME=PF=x-1,MF=BE=2,进而可得出EF=x+1,结合EF为点P纵坐标的绝对值,即可得出关于x的一元二次方程,解之即可求出x的值,取其大于1的值代入点P的坐标中即可得出结论.
【详解】
解:(1)设抛物线的解析式为y=a(x﹣1)2﹣4,
将C(0,﹣3)代入y=a(x﹣1)2﹣4,得:﹣3=a(0﹣1)2﹣4,
解得:a=1,
∴抛物线的解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3.
(2)当y=0时,有x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0).
设抛物线对称轴与x轴交于点E,过点P作PF∥x轴,交抛物线对称轴于点F,如图所示.
设点P的坐标为(x,x2﹣2x﹣3)(x>1),则PF=x﹣1,BE=3﹣1=2.
∵∠BME+∠PMF=90°,∠BME+∠MBE=90°,
∴∠MBE=∠PMF.
在△MBE和△PMF中, ,
∴△MBE≌△PMF(AAS),
∴ME=PF=x﹣1,MF=BE=2,
∴EF=ME+MF=x+1.
∵EF=|x2﹣2x﹣3|,
∴|x2﹣2x﹣3|=x+1,即x2﹣3x﹣4=0或x2﹣x﹣2=0,
解得:x1=﹣1(舍去),x2=2,x3=4,
∴点P的坐标为(2,﹣3)或(4,5).
【点睛】
本题考查待定系数法求二次函数解析式、二次函数图象上点的坐标特征、全等三角形的判定与性质以及解一元二次方程,解题关键是:(1)根据点的坐标特征,利用待定系数法求出二次函数解析式;(2)利用全等三角形的性质及二次函数图象上点的坐标特征,找出关于x的一元二次方程.
23.(1)证明见解析;(2)①证明见解析;②1
【分析】
(1)根据题意,得四边形是平行四边形;根据平行线和角平分线性质,推导得,结合等腰三角形和菱形的性质,即可完成证明;
(2)①过O作交于N,根据矩形性质,通过证明四边形是矩形,得,;根据梯形中位线的性质,得为的中点,;通过证明,得,根据等腰三角形性质,得,通过计算即可完成证明;②过O作垂直于M,根据正方形性质,通过证明四边形是正方形,得,,;根据直角三角形斜边中线性质,得;根据三角形中位线的性质,推导得;结合题意,通过计算得;再根据含角的直角三角形性质,即可得到答案.
【详解】
(1)∵,
四边形是平行四边形
∴,
,
∵平分,
,
,
∴,
平行四边形是菱形;
(2)①过O作交于N,如图4所示:
,,,
四边形是矩形
,,
,
∵为的中点,
为的中点,,
∴
,
.
∵,
.
②过O作垂直于M,如图5所示:
∵四边形是平行四边形,,,
四边形是正方形
∴,,,
∵为的中点,
.
∵,
,
是的中位线,
∵,
,
由(2)①得:,
.
【点睛】
本题考查了平行线、角平分线、平行四边形、菱形、等腰三角形、矩形、梯形中位线、全等三角形、直角三角形斜边中线、含角的直角三角形、三角形中位线的知识;解题的关键是熟练掌握菱形、正方形、等腰三角形、直角三角形斜边中线、含角的直角三角形、三角形中位线的性质,从而完成求解.
2022年云南省昆明市禄劝县初中学业水平模拟数学试卷(二)(word版含答案): 这是一份2022年云南省昆明市禄劝县初中学业水平模拟数学试卷(二)(word版含答案),共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022年云南省昆明市初中学业水平考试联考数学试题(一)(word版含答案): 这是一份2022年云南省昆明市初中学业水平考试联考数学试题(一)(word版含答案),共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022年云南省昆明市呈贡区初中学业水平第一次模拟考试数学试题(word版含答案): 这是一份2022年云南省昆明市呈贡区初中学业水平第一次模拟考试数学试题(word版含答案),共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












