高中数学人教A版 (2019)必修 第二册7.1 复数的概念教学演示ppt课件

这是一份高中数学人教A版 (2019)必修 第二册7.1 复数的概念教学演示ppt课件，共25页。PPT课件主要包含了旧知导入，数系的扩充，用图形表示包含关系，自然数，有理数，无理数，增加新元素，思考3，复数的概念，复数的代数形式等内容，欢迎下载使用。

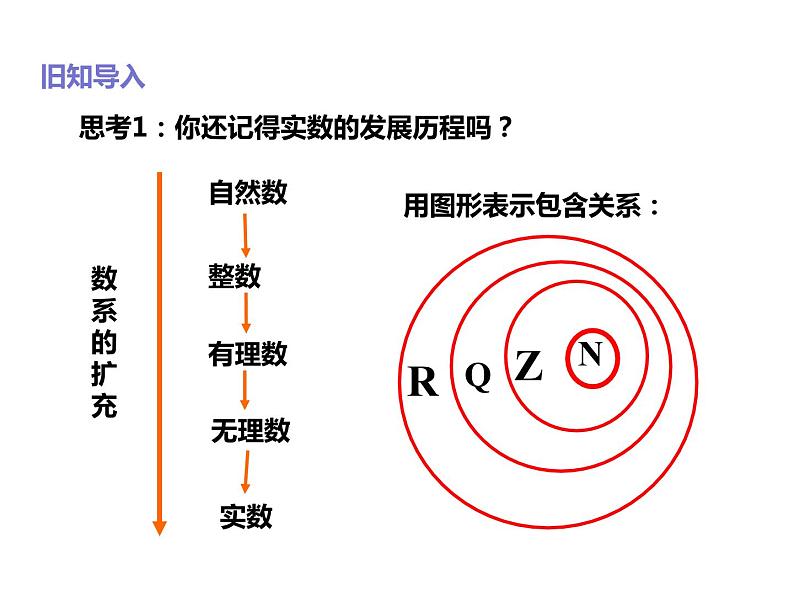
思考1：你还记得实数的发展历程吗？
思考2：为什么要将数系进行扩充？
数系每次扩充的基本原则：
第二、原有的运算性质仍然成立；
第三、新数系能解决旧数系中的矛盾.
方程无实数解；因为负实数不能开平方。
为了解决正方形对角线的度量，以及 这样的方程在有理数集中无解的问题，人们把有理数集扩充到了实数集。根据这个方法，为了使负实数也能开平方，我们将数系进行扩充。
依照这种思想，为了解决 这样的方程在实数系中无解的问题，我们设想引入一个新数i，使得x=i是方程的解。
思考4：把新引进的数i添加到实数集中，我们希望数i和实数之间仍然能像实数那样进行加法和乘法运算，并希望加法和乘法满足交换律、结合律，以及乘法对加法满足分配率。 那么，实数系经过扩充后，得到的新数系由哪些数组成呢？
依照以上设想，把实数b与i相乘，结果记作bi；把实数a与bi相加，结果记作a+bi.
思考5：以上这些数有什么特点呢？
所有实数以及i都可以写成a+bi 的形式，从而这些数都在扩充后的新数集中。
知识探究（一）：数系的扩充和复数的概念
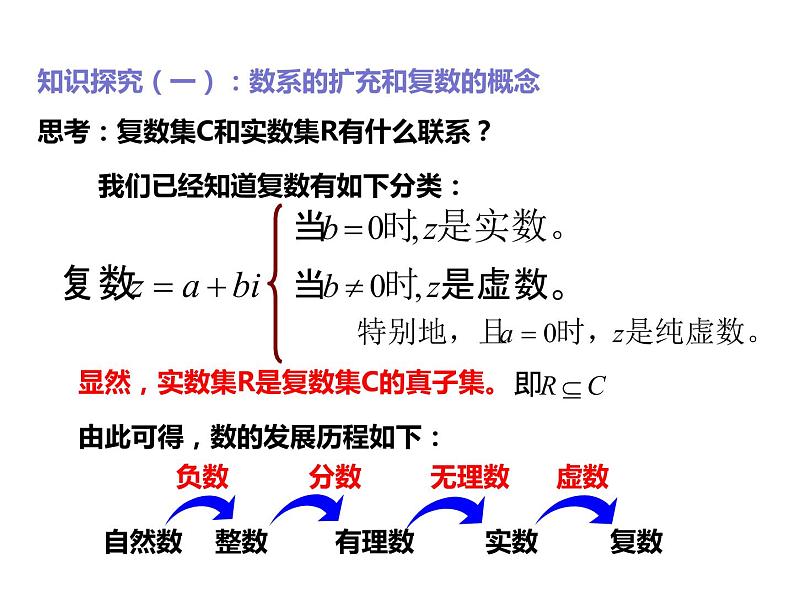
思考：复数集C和实数集R有什么联系？
我们已经知道复数有如下分类：
显然，实数集R是复数集C的真子集。
由此可得，数的发展历程如下：
1、判一判(正确的打“√”，错误的打“×”)
(1)若a，b为实数，则z＝a＋bi为虚数．( 　　) (2)若z＝m＋ni(m，n∈C)，则当且仅当m＝0，n≠0时，z为纯虚数．(　 　) (3)bi是纯虚数．(　 ) (4)如果两个复数的实部的差和虚部的差都等于0，那么这两个复数相等．(　 　)
2、判断以下复数哪些是虚数？哪些是纯虚数；并说出实部和虚部。
解决复数相等问题的步骤是：分别分离出两个复数的实部和虚部，利用实部与实部相等、虚部与虚部相等列方程(组)求解．
思考1:我们知道，实数与数轴上的点一一对应，因此实数可以用数轴上的点来表示。那么，复数有什么几何意义呢？
知识探究（二）：复数的几何意义
这个建立了直角坐标系来表示复数的平面叫做复平面。x轴叫做实轴，y轴叫做虚轴。
显然，实轴上的点都表示实数；除了原点外，虚轴上的点都表示纯虚数。
按照这种表示方法，每一个复数，有复平面内唯一的一个点与它对应；反过来，复平面内的每一个点，有唯一的一个复数与它对应。
由此可知，复数集C中的数与复平面内的点按如下方式建立了一一对应关系。
这就是复数的第一种几何意义。
思考2:在平面直角坐标系中，每一个平面向量都可以用一个有序实数对来表示，而有序实数对与复数是一一对应的，那么，你能用平面向量来表示复数吗？
这就是复数的另一种几何意义。
一般地，当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数。虚部不等于0的两个共轭复数也叫做共轭复数。
横坐标相等，纵坐标互为相反数。
1、已知 x 是实数，y 是纯虚数，且满足 ，求 x 与 y．
2、在实数与复数范围内, 讨论关于x的一元二次方程 (a、b、c∈R, a≠0)的根的情况。
解：∵∆=b2-4ac 当∆=0时，有两相等实根；当∆>0时，有两不等实根；当∆<0时，b2-4ac<0,4ac-b2>0，∆=i2（4ac-b2）
3、设复数z = a + bi (a，b∈R)和复平面上的点Z (a，b)对应，a，b必须满足什么条件，才能使点Z位于：（1）实轴上？（2）虚轴上（不含原点）？（3）上半平面（含实轴）？（4）左半平面（不含虚轴）？