




人教版九年级下册27.2.2 相似三角形的性质图文ppt课件
展开1.知道三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.2.知道相似三角形对应线段的比等于相似比. 3.知道相似三角形面积的比等于相似比的平方.
1.什么叫做相似三角形?
2.你有几种方法判定两个三角形是相似三角形?
对应边成比例,对应角相等的三角形是相似三角形.
(1)两角分别相等的两个三角形相似.(2)两边成比例且夹角相等的两个三角形相似.(3)三边成比例的两个三角形相似.
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论.例如,在下图中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD,A′D′分别为BC,B′C′边上的高,那么AD,A′D′之间有什么关系?
△ABD和△A′B′D′都是直角三角形,而∠B=∠B′,因为有两个角对应相等,所以这两个三角形相似.那么
相似三角形对应高的比等于相似比.
那么,相似三角形对应角平分线、对应中线的比等于相似比吗?
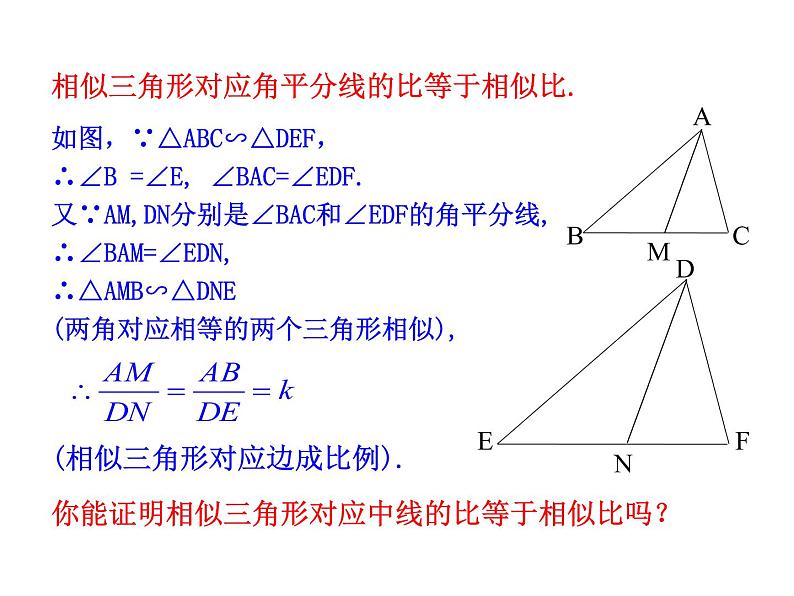
如图,∵△ABC∽△DEF,∴∠B =∠E, ∠BAC=∠EDF.又∵AM,DN分别是∠BAC和∠EDF的角平分线,∴∠BAM=∠EDN,∴△AMB∽△DNE (两角对应相等的两个三角形相似),
相似三角形对应角平分线的比等于相似比.
(相似三角形对应边成比例).
你能证明相似三角形对应中线的比等于相似比吗?
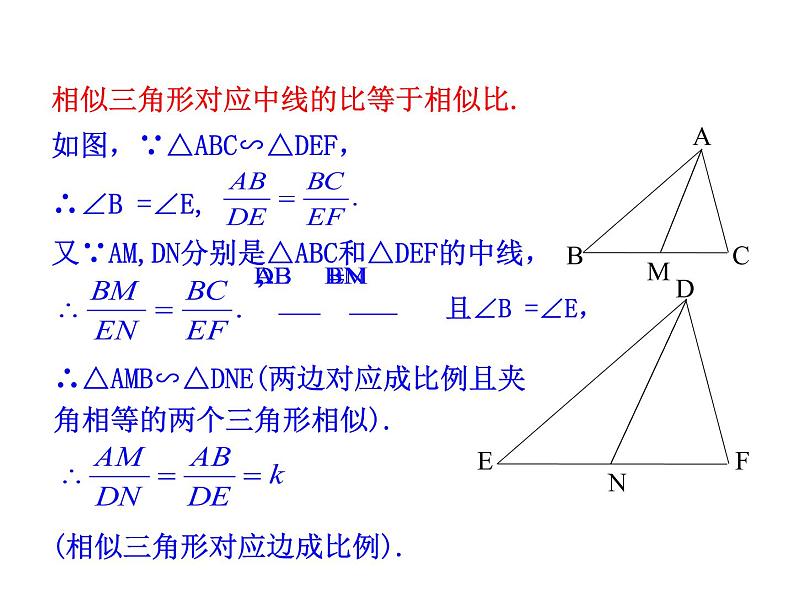
如图,∵△ABC∽△DEF,∴∠B =∠E,
相似三角形对应中线的比等于相似比.
又∵AM,DN分别是△ABC和△DEF的中线,
∴△AMB∽△DNE(两边对应成比例且夹角相等的两个三角形相似).
定理:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
如果△ABC和△A′B′C′是两个相似三角形,相似比为k,那么
定理:相似三角形的周长比等于相似比.
相似三角形的面积比与相似比有什么关系?
如果△ABC和△A′B′C′是两个相似三角形,相似比为k,高为AD,A′D′那么
根据三角形的面积计算公式及定理1,得
定理:相似三角形的面积比等于相似比的平方.
下图中(1)、(2)、(3)分别是边长为1,2,3的等边三角形,它们都相似.
(2)与(1)的相似比=__________,(2)与(1)的面积比=__________,(3)与(1)的相似比=__________,(3)与(1)的面积比=__________.
1.如果两个三角形相似,相似比为3∶5,那么对应角平分线的比等于多少?______.2.相似三角形对应边的比为0.4,那么相似比为______,对应角平分线的比为______,周长的比为______,面积的比为______.
3.若两个三角形面积之比为16:9,则它们的对应高之比为________,对应中线之比为________.
1.已知两个三角形相似,请完成下列表格:
2.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( )A. 1:2 B. 1:4 C. 2:1 D. 4:1
3.下列命题中,是假命题的是( ) A.全等三角形的对应边相等 B.两角和一边分别对应相等的两个三角形全等C.对应角相等的两个三角形全等 D.相似三角形的面积比等于相似比的平方
4.△ABC与△A′B′C′的相似比为3:4,若BC边上的高AD=12cm,则B′C′边上的高A′D′ =______ .5.△ABC与△A′B′C′ 的相似比为1:5,如果A′C′边上的中线B′D′=20cm,则AC边上的中线BD=____ .6.如图△ABC∽△A′B′C′,对应中线AD=6cm,A′D′=10cm,若BC=4.2cm,则B′C′=______.
初中数学人教版九年级下册27.2.2 相似三角形的性质课文配套ppt课件: 这是一份初中数学人教版九年级下册27.2.2 相似三角形的性质课文配套ppt课件,共30页。PPT课件主要包含了复习引入,角平分线,合作探究,试一试,典例精析,练一练,想一想,相似三角形面积的比,又∵∠D∠A等内容,欢迎下载使用。
初中数学人教版九年级下册27.2.2 相似三角形的性质背景图课件ppt: 这是一份初中数学人教版九年级下册27.2.2 相似三角形的性质背景图课件ppt,共21页。PPT课件主要包含了猜想和探究,生成与挖掘,辨析结论,练习1,例题与练习,练习2,提高与拓展,答案1︰6,课堂小结与作业布置,课堂小结等内容,欢迎下载使用。
初中数学第二十七章 相似27.2 相似三角形27.2.2 相似三角形的性质说课课件ppt: 这是一份初中数学第二十七章 相似27.2 相似三角形27.2.2 相似三角形的性质说课课件ppt,共30页。PPT课件主要包含了复习引入,角平分线,合作探究,试一试,典例精析,练一练,想一想,相似三角形面积的比,又∵∠D∠A等内容,欢迎下载使用。













