人教版数学中考复习《抛物线下四边形问题》教学课件ppt课件

这是一份人教版数学中考复习《抛物线下四边形问题》教学课件ppt课件，共17页。PPT课件主要包含了方法指导，真题回顾，试题分析，满分解答，变式训练等内容，欢迎下载使用。

抛物线下四边形问题作为代数和几何相结合 的一个重要内容，历来都是中考的必争之地 其中抛物线与特殊四边形存在探究问题更是 将数形结合的数学思想体现得淋漓尽致.现 将此类问题在近年中考的常见题型加以归类 剖析解法，以供借鉴.在此类问题设计上大 都表现在抛物线下四边形的性质上，往往和 特殊四边形相融合，判断四边形的存在性、 形状、性质、特殊角的大小及其面积最大值 最小值等，考点主要包括：
抛物线下特殊四边形的存在性问题；抛物线下四边形的最值问题；抛物线下特殊四边形的运动变化；抛物线下特殊四边形的其他问题等.
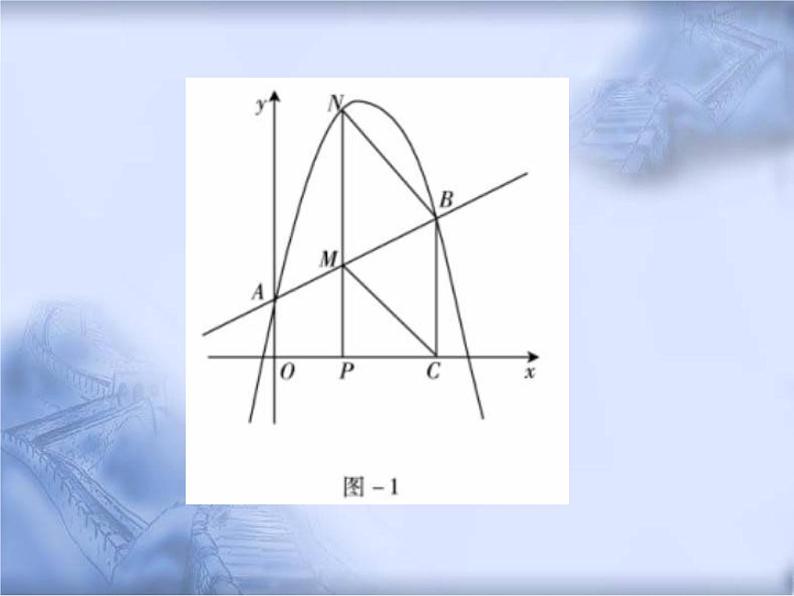
例（2011•广东）如图-1，抛物线y=- 5/4x2+174x+1与y轴交于点A，过点A的直线 与抛物线交于另一点B，过点B作BC⊥x轴， 垂足为点C（3，0）.求直线AB的表达式；动点P在线段OC上从原点出发以每秒一 个单位的速度向点C移动，过点P作PN⊥x轴， 交直线AB于点M，交抛物线于点N.设点P移动 的时间为t秒，MN的长度为s个单位，求s与t 的函数表达式，并写出t的取值范围；
（3）设在（2）的条件下（不考虑点P与点O 和点C重合的情况），连接CM，BN，当t为何 值时，四边形BCMN为平行四边形？问对于所 求的t值，平行四边形BCMN是否为菱形？请 说明理由.
1.如图-2，已知抛物线y=x2-4x+3与x轴交 于两点A，B，其顶点为C.对于任意实数m，点M（m，-2）是否在 该抛物线上？请说明理由；求证：△ABC是等腰直角三角形；已知点D在x轴上，那么在抛物线上是 否存在点P，使得以B，C，D，P为顶点的四 边形是平行四边形？若存在，求出点P的坐 标；若不存在，请说明理由.
2.在平面直角坐标系中，抛物线y=x2+5x+4的顶点 为M，与x轴交于A，B两点（点A在点B左侧），与y 轴交于点C.求点A，B，C的坐标；求抛物线y=x2+5x+4关于坐标原点O对称的抛 物线的表达式；设（2）中所求抛物线的顶点为M′，与x轴 交于A′，B′两点，与y轴交于C′点，在以A，B， C，M，A′，B′，C′，M′这八个点中的四个点 为顶点的平行四边形中，求其中一个不是菱形的 平行四边形的面积.