人教版数学中考复习《四边形》教学课件ppt课件

这是一份人教版数学中考复习《四边形》教学课件ppt课件，共18页。PPT课件主要包含了四边形，一个角是，有关定理，外角和等于，n边形的内角和等于，梯形的中位线，于两底且等于，夹在两条平行线间的，夹在间的垂线段相等，主要画图等内容，欢迎下载使用。

一、四边形的分类及转化二、几种特殊四边形的性质三、几种特殊四边形的常用判定方法四、中心对称图形与中心对称的区别和联系 五、有关定理六、主要画图 七、典型举例
两组对边平行平行四边形
一组对边平行另一组对边不平行
一、四边形的分类及转化
互相垂直平分，且每一 条对角线平分一组对角
中心对称图形 轴对称图形
互相垂直平分且相等，每 中心对称图形 一条对角线平分一组对角 轴对称图形
二、几种特殊四边形的性质：
三、几种特殊四边形的常用判定方法：
四、中心对称图形与中心对称的区别和联系
中心对称图形：如果把一个图形绕着某一
点旋转180°后与原来的图 形重合，那么这个图形叫 做中心对称图形，这个点 叫做对称中心。
中心对称：如果把一个图形绕着某一 点旋转180°后与另一个图 形重合，那么这两个图形 关于这个点中心对称，这 个点叫做对称中心。
1、中心对称的两个图形是全等图形
2、中心对称的两个图形的对称点连线通过对称中心，且被对称中心平分
中心对称图形的对称点连线通过 对称中心，且被对称中心平分
1、四边形的内角和等于
（n - 2）180°
条件：在梯形ABCD中，EF是中位线
3、两条平行线之间的距离以及性质：两条平行线中，一条直线上任意一点到另一条 直线的距离，叫这两条平行线的距离。
结论：EF∥AB∥CD，EF=
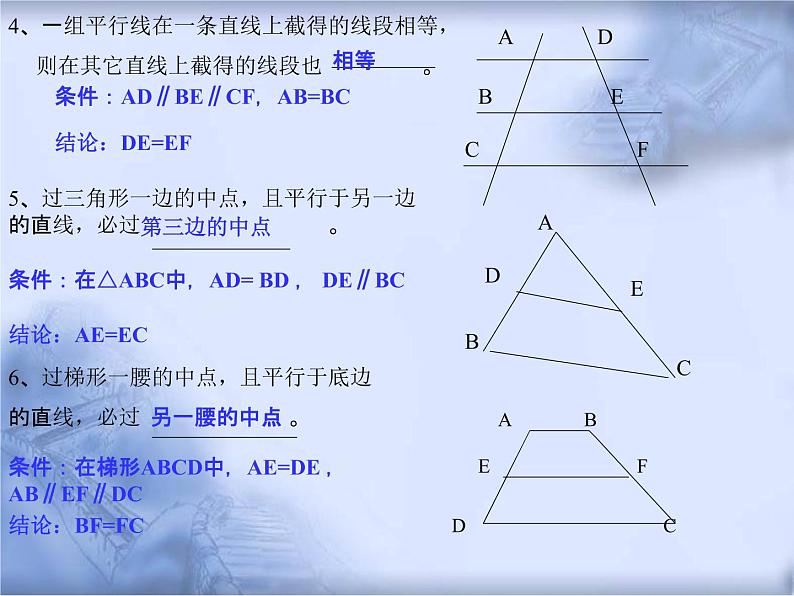
条件：AD∥BE∥CF，AB=BC
条件：在梯形ABCD中，AE=DE ，AB∥EF∥DC结论：BF=FC
4、一组平行线在一条直线上截得的线段相等， 则在其它直线上截得的线段也 相等。
5、过三角形一边的中点，且平行于另一边 的直线，必过第三边的中点。条件：在△ABC中，AD= BD ， DE∥BC
6、过梯形一腰的中点，且平行于底边 的直线，必过 另一腰的中点 。
1、画平行四边形、矩形、菱形、正方形、等腰梯形如：画一个平行四边形ABCD，使边BC=5cm, 对角线AC=5cm，BD=8cm.
如图：点C就是线段AB的中点
如图：点D、E、F、H就是线段AB的 五等分点
例1：如图，四边形ABCD为平行四边形，延长BA至E，延长DC至F，
使BE=DF，AF交BC于H，CE交AD于G. 求证：∠E=∠F
四边形AFCE是平行四边形
注：利用平行四边形的性质来证明线段或角相等是一种常用方法。
例2：如图，在四边形ABCD中，AB=2，CD=1，∠A=60°， ∠B= ∠D=90 °，求四 边形ABCD的面积。
注：四边形的问题经常转化为三角形的问题来解，转化的方法是添加适当的辅助线， 如连结对角线、延长两边等。
延长AD，BC交于点E，
∵在Rt△ABE中，∠A=60°，∴∠E=30°又∵AB=2∴BE=√3AB=2 √3
∵在Rt△CDE中，同理可得
∴S四边形ABCD=S Rt△ABE- S Rt△CDE
= AB·BE -CD·DE 22
例3：如图，在梯形ABCD中，AB∥CD，中位线EF=7cm，对角线AC⊥BD，∠BDC=30°，求梯形的高线AH
析：求解有关梯形类的题目，常需添加辅助线，把问题转化 为三角形或四边形来求解，添加辅助线一般有下列所示的几 E 种情况：
过梯形一腰中点和上底 一端作直线
例3：如图，在梯形ABCD中，AB∥CD，中位线EF=7cm，对角线AC⊥BD，
∠BDC=30°，求梯形的高线AH
过A作AM∥BD，交CD的延长线 于M
又∵AB∥CD∴四边形ABDM是平行四边形，∴DM=AB，∠AMC= ∠BDC=30°又∵中位线EF=7cm，∴CM=CD+DM=CD+AB=2EF=14cm又∵AC⊥BD，∴AC⊥AM，∵AH⊥CD，∠ACD=60°
∴AH=AC·sin60°=
例4：已知，如图，矩形纸片长为8cm，宽为6cm, 把纸对折使相对两顶点A，C 重合，求折痕的长。
D解： 设折痕为EF，连结AC，AE，CF，若A，C两点 重合，它们必关于EF对称，则EF是AC的中垂线 ，
故AF=FC，设AC与EF交于点O，AF=FC=xcm
∴AF=FC=,2F5D=8 – x=
答：折痕的长为7.5cm注：①解“翻折图形”问题的关键是要认识到对折时折痕为重合两点的对 称轴，会形成轴对称图形。②本题通过设未知数，然后根据图形的几何元素间的关系列方程求解的方 法，是数学中常用的“方程思想”。
则FD=AD – AF=8 - x
∵在Rt△CDF中，FC2 = FD2 + CD2解得x= 7
∴x=2 （8 - x）+
在Rt△FEH中，EF2 = FH2 + EH2
∴EF=±7.5(负根舍去）
例4：已知，如图，矩形纸片长为8cm，宽为6cm, 把纸对折使相对两顶点A，C 重合，求折痕的长。解法2