人教版数学中考复习专题《抛物线下线段和三角形问题》精品教学课件ppt优秀课件

这是一份人教版数学中考复习专题《抛物线下线段和三角形问题》精品教学课件ppt优秀课件，共21页。PPT课件主要包含了真题回顾，试题分析，满分解答，变式训练等内容，欢迎下载使用。

方法指导根据近几年的中考试卷，在所有的压轴题里面， 以二次函数为载体，结合几何图形的题型是中考 的热点和难点，解答此类试题需要用到的数学思 想如下：（1）函数思想；（2）数形结合思想；（3）转化 思想；（4）分类讨论思想.二次函数综合题，主要是以二次函数为主线，利 用函数的图象与性质，结合二次函数的图象信息 和点在函数图象上即点的坐标满足函数表达式等.：
解题策略：应用函数思想解题，确立变量之间的 函数表达式是关键步骤，主要分为下面四种情况：根据题意建立变量之间的函数表达式，把问 题转化为相应的函数问题；用待定系数法求函数表达式；利用两个三角形相似解决最值问题；动点与图形面积的关系，动点与线段之和最 短问题的关系.
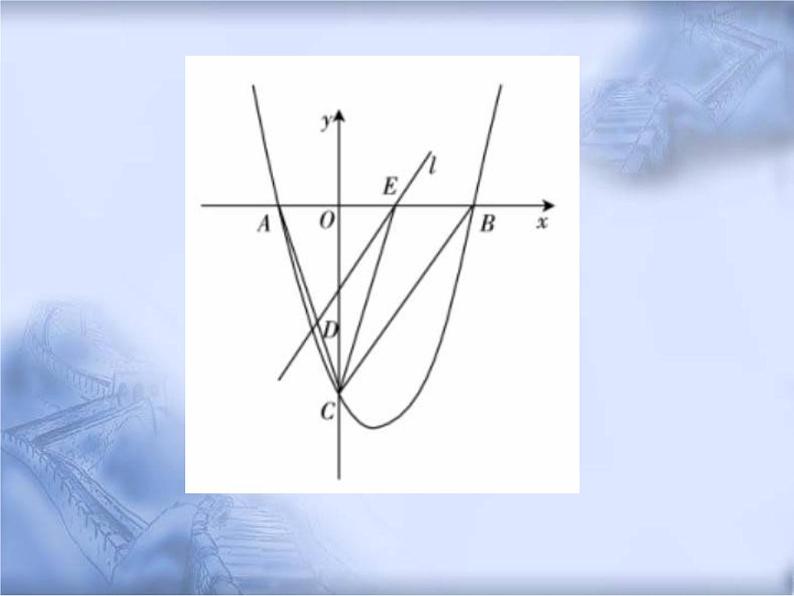
例（2012•广东）如图-1，抛物线y=12x2-32x-9与x轴交于A，B 两点，与y轴交于点C，连接BC，AC.求AB和OC的长；点E从点A出发，沿x轴向点B运动（点E与点A，B不重合）， 过点E作直线l平行BC，交AC于点D.设AE的长为m，△ADE的面积为S，求S关于m的函数表达式，并写出自变量m的取值范围；在（2）的条件下，连接CE，求△CDE面积的最大值；此时， 求出以点E为圆心，与BC相切的圆的面积（结果保留π）.
本题考查了学生对函数与其图象的认识及提取信息的能 力，用到的知识点有二次函数的性质、相似三角形的性 质、图形面积的求法等等，总体来说难度不高.具体可分 析如下：已知抛物线的表达式，当x=0时，可确定点C的坐标；当y=0时，可确定点A，B的坐标，进而确定AB，OC的长；直线l∥BC，可得出△AED与△ABC相似，则它们的 面积比等于相似比的平方.由此得到关于S，m的函数表达 式；根据点E与点A，B不重合可确定m的取值范围；
（3）①首先用含m的式子表示出△AEC的面积，又△AEC，△AED的面积差即为△CDE的面积，由此可 得关于S△CDE，m的函数表达式，然后根据函数的 性质可得到S△CDE的最大面积以及此时m的值；② 过点E作BC的垂线EM，这个垂线段的长即为与BC相 切的⊙E的半径，可根据相似三角形△BEM，△BCO 得到的相关比例线段求得该半径的值，由此得解.
1.（2015•黔东南州）如图-3，已知二次函数y1=- x2+134x+c的图象与x轴的一个交点为A（4，0）， 与y轴的交点为B，过点A，B的直线为y2=kx+b.求二次函数y 1的表达式及点B的坐标；由图象写出满足y1＜y2的自变量x的取值范 围；在两坐标轴上是否存在点P，使得△ABP是以 AB为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由.
2.（2015•青海）如图-4，二次函数y=ax2+bx-3的 图象与x轴交于A（-1，0），B（3，0）两点，与y 轴交于点C，该抛物线的顶点为M.求该抛物线的表达式；判断△BCM的形状，并说明理由；探究坐标轴上是否存在点P，使得以点P，A，C为顶点的三角形与△BCM相似.若存在，请直接 写出点P的坐标；若不存在，请说明理由.