2021年浙江省宁波市中考数学冲刺试卷（一）

这是一份2021年浙江省宁波市中考数学冲刺试卷（一），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2021年浙江省宁波市中考数学冲刺试卷（一）
一、选择题（每小题4分，共40分，在每小题给出的四个选项中，只有一项符合题目要求）
1．（4分）的绝对值是（　　）
A．﹣3 B． C．3 D．
2．（4分）下列运算结果为a6的是（　　）
A．a3•a2 B．a9﹣a3 C．（a2）3 D．a18÷a3
3．（4分）截止北京时间2020年4月11日21时许，全球累计新冠确诊病例数已超171万例．将1710000用科学记数法表示（　　）
A．1.71×105 B．0.171×107 C．1.71×106 D．1710000
4．（4分）一个袋子中装有6个黑球3个白球，这些球除颜色外，形状、大小、质地等完全相同，在看不到球的条件下，随机地从这个袋子中摸出一个球，摸到白球的概率为（　　）
A． B． C． D．
5．（4分）如图，已知a∥b，一块含30°角的直角三角板，如图所示放置，∠2＝30°，则∠1等于（　　）

A．110° B．130° C．150° D．160°
6．（4分）如图，在⊙O中，∠C＝30°，OA＝2，则弧AB的长为（　　）

A． B． C． D．π
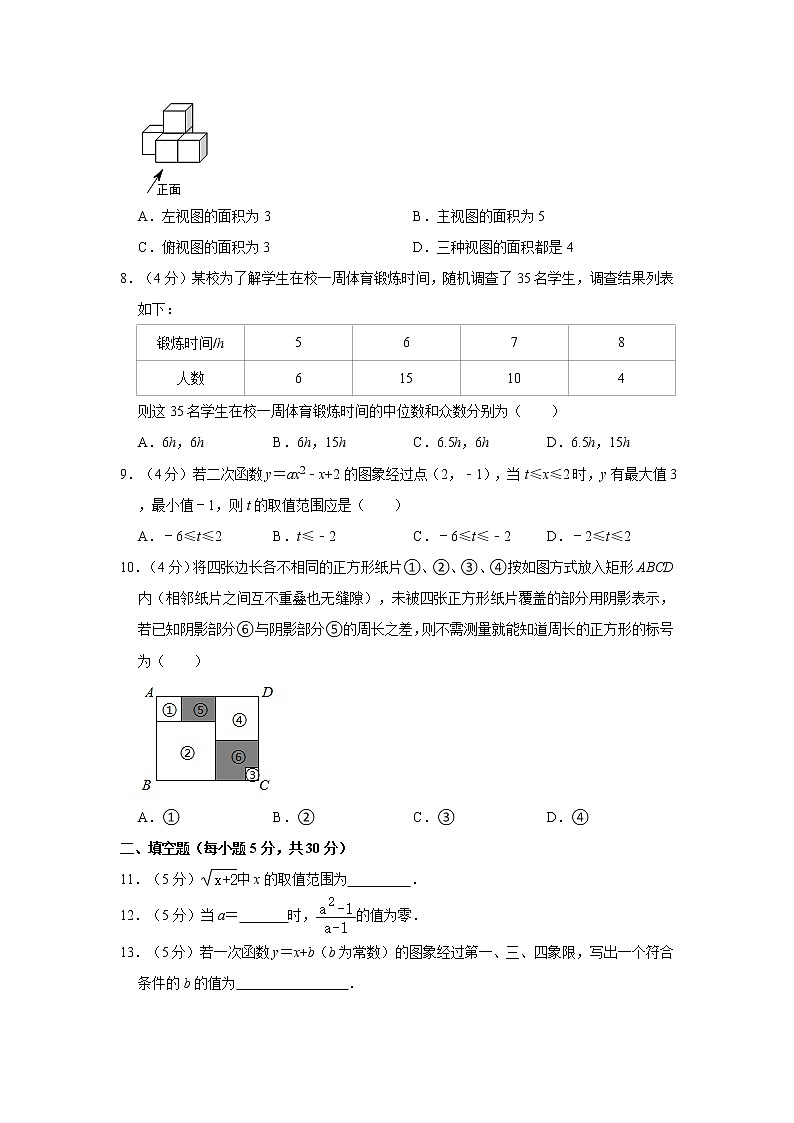
7．（4分）如图是一个由5个棱长为1的小正方形搭成的几何体，下列说法正确的是（　　）

A．左视图的面积为3 B．主视图的面积为5
C．俯视图的面积为3 D．三种视图的面积都是4
8．（4分）某校为了解学生在校一周体育锻炼时间，随机调查了35名学生，调查结果列表如下：
锻炼时间/h
5
6
7
8
人数
6
15
10
4
则这35名学生在校一周体育锻炼时间的中位数和众数分别为（　　）
A．6h，6h B．6h，15h C．6.5h，6h D．6.5h，15h
9．（4分）若二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），当t≤x≤2时，y有最大值3，最小值﹣1，则t的取值范围应是（　　）
A．﹣6≤t≤2 B．t≤﹣2 C．﹣6≤t≤﹣2 D．﹣2≤t≤2
10．（4分）将四张边长各不相同的正方形纸片①、②、③、④按如图方式放入矩形ABCD内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示，若已知阴影部分⑥与阴影部分⑤的周长之差，则不需测量就能知道周长的正方形的标号为（　　）

A．① B．② C．③ D．④
二、填空题（每小题5分，共30分）
11．（5分）中x的取值范围为　 　．
12．（5分）当a＝　 　时，的值为零．
13．（5分）若一次函数y＝x+b（b为常数）的图象经过第一、三、四象限，写出一个符合条件的b的值为　 　．
14．（5分）已知x和y满足方程组，则代数式9x2﹣4y2的值为　 　．
15．（5分）如图，Rt△ACB中，∠C＝90°，AC＝BC＝6，点O在BC边上，且OB＝2，P是AB边上的动点，连接OP，以点O为圆心，OP长为半径为作⊙O．当⊙O与Rt△ACB的边相
切时，BP的长为　 　．

16．（5分）如图，矩形ABCD中，点A在函数y＝（k＞0，x＞0）的图象上，点B，C在x轴上，AD交y轴于点F，延长CD至点E，使CD＝3DE，连接BE交y轴于点P，连接PC，PA．若△PCB的面积为5，则k的值为　 　，△POC的面积与△PFA的面积差为　 　．

三、解答题（本大题有8小题，共80分）
17．（8分）（1）计算：（x+2）2﹣x（x﹣3）．
（2）解不等式：≥﹣2．
18．（8分）图1、图2是6×6的方格纸，点A，B都在格点上，按要求画图：

（1）请在图1中画一个五边形ABCDE，且是轴对称图形．
（2）请在图2中画一个六边形ABCDEF，且是中心对称图形．
19．（8分）如图，小明想在自己家的窗口A处测量对面建筑物CD的高度，他首先测量出窗口A到地面的距离AB＝16m，又测得从A处看建筑物底部C的俯角为α＝30°，看建筑物顶部D的仰角为β＝45°，且AB，CD都与地面垂直，点A，B，C，D在同一平面内．
（1）求AB与CD之间的距离（结果保留根号）；
（2）求建筑物CD的高度（结果精确到0.1m）．（参考数据：≈1.41，≈1.73）

20．（10分）如图，二次函数y＝（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y＝kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．
（1）求二次函数的表达式及点B的坐标．
（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．

21．（10分）为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下尚不完整的统计图表．
调查结果统计表
组别
分组（单位：元）
人数
A
0≤x≤30
8
B
30＜x≤60
32
C
60＜x≤90
a
D
90＜x≤120
16
E
x＞120
4
请根据以上图表，解答下列问题：
（1）这次被调查的同学共有　 　人，a＝　 　，m＝　 　；
（2）求扇形统计图中C所在的扇形的圆心角度数；
（3）该校共有学生2000人，请估计每月零花钱的数额x在60＜x≤120范围内的人数．

22．（10分）某校学生食堂共有座位3600个，某天午餐时，食堂中学生人数y（人）与时间x（分钟）变化的函数关系图象如图中的折线OAB．
（1）试分别求出当0≤x≤20与20≤x≤38时，y与x的函数关系式；
（2）已知该校学生数有6000人，考虑到安全因素，学校决定对剩余2400名同学延时用餐，即等食堂空闲座位不少于2400个时，再通知剩余2400名同学用餐．请结合图象分析，这2400名学生至少要延时多少分钟？

23．（12分）【基础巩固】
（1）如图1，在四边形ABCD中，点P为AB上一点，∠DPC＝∠A＝∠B＝90°，求证：AD•BC＝AP•BP．
【尝试应用】
（2）如图2，在边长为4的菱形ABCD中，∠ABC＝60°，E为对角线BD上一点，且BE＝2DE，F为AD上一点，∠AEF＝30°，求AF的长．
【拓展提高】
（3）如图3，等边△DEF内接于矩形ABCD，其中点E，F分别在边AB，BC上，若BE＝4，CD＝5，求等边△DEF的边长．

24．（14分）定义：有一组对角互余的凸四边形称为对余四边形．
（1）如图1，在11×7的网格中，点A，B，D都是网格的格点，请你确定所有格点C，使得四边形ABCD是对余四边形．
（2）如图2，EF是⊙O的直径，点A，D，C在⊙O上，AF，CE相交于点B．求证：四边形ABCD是对余四边形．
（3）已知四边形ABCD是对余四边形．
①如图3，若DA＝DB，BC＝2，CD＝4，AC＝6，求∠DAB的度数；
②在平面直角坐标系中，设点A（﹣1，0），B（3，0），C（1，2），求线段DO长度的取值范围．

2021年浙江省宁波市中考数学冲刺试卷（一）
参考答案与试题解析
一、选择题（每小题4分，共40分，在每小题给出的四个选项中，只有一项符合题目要求）
1．（4分）的绝对值是（　　）
A．﹣3 B． C．3 D．
【分析】根据绝对值的定义直接进行计算．
【解答】解：根据绝对值的概念可知：|﹣|＝，
故选：B．
2．（4分）下列运算结果为a6的是（　　）
A．a3•a2 B．a9﹣a3 C．（a2）3 D．a18÷a3
【分析】分别根据同底数幂的乘法法则，合并同类项法则，幂的乘方运算法则以及同底数幂的除法法则逐一判断即可．
【解答】解：A．a3•a2＝a5，故本选项不合题意；
B．a9与﹣a3不是同类项，所以不能合并，故本选项不合题意；
C．（a2）3＝a6，故本选项符合题意；
D．a18÷a3＝a15，故本选项不合题意．
故选：C．
3．（4分）截止北京时间2020年4月11日21时许，全球累计新冠确诊病例数已超171万例．将1710000用科学记数法表示（　　）
A．1.71×105 B．0.171×107 C．1.71×106 D．1710000
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【解答】解：将数据1710000用科学记数法表示为：1.71×106．
故选：C．
4．（4分）一个袋子中装有6个黑球3个白球，这些球除颜色外，形状、大小、质地等完全相同，在看不到球的条件下，随机地从这个袋子中摸出一个球，摸到白球的概率为（　　）
A． B． C． D．
【分析】用白球的个数除以总球的个数即可得出答案．
【解答】解：∵袋子中装有6个黑球3个白球，共有9个球，
∴摸到白球的概率为＝；
故选：C．
5．（4分）如图，已知a∥b，一块含30°角的直角三角板，如图所示放置，∠2＝30°，则∠1等于（　　）

A．110° B．130° C．150° D．160°
【分析】利用三角形外角与内角的关系，先求出∠3，利用平行线的性质得到∠4的度数，再利用三角形外角与内角的关系求出∠1．
【解答】解：∵∠C＝90°，∠2＝∠CDE＝30°，
∠3＝∠C+∠CDE
＝90°+30°
＝120°．
∵a∥b，
∴∠4＝∠3＝120°．
∵∠A＝30°
∴∠1＝∠4+∠A
＝120°+30°
＝150°．
故选：C．

6．（4分）如图，在⊙O中，∠C＝30°，OA＝2，则弧AB的长为（　　）

A． B． C． D．π
【分析】根据圆周角定理求出圆心角∠AOB的度数，然后根据弧长公式求解即可．
【解答】解：∵∠C＝30°，
根据圆周角定理可知：∠AOB＝60°，
∵OA＝2，
∴l＝＝，
∴弧AB的长为π．
故选：A．
7．（4分）如图是一个由5个棱长为1的小正方形搭成的几何体，下列说法正确的是（　　）

A．左视图的面积为3 B．主视图的面积为5
C．俯视图的面积为3 D．三种视图的面积都是4
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，看分别得到几个面，即可作出判断．
【解答】解：A、从左面看，底层是2个正方形，上层左边是1个正方形，所以面积为3，故本选项符合题意；
B、从正面看，底层是3个正方形，上层中间是1个正方形，所以面积为4，故本选项不合题意；
C、从上面看，底层是2个正方形，上层是2个正方形，所以面积为4，故本选项不合题意；
D、左视图的面积为3，故本选项不合题意．
故选：A．
8．（4分）某校为了解学生在校一周体育锻炼时间，随机调查了35名学生，调查结果列表如下：
锻炼时间/h
5
6
7
8
人数
6
15
10
4
则这35名学生在校一周体育锻炼时间的中位数和众数分别为（　　）
A．6h，6h B．6h，15h C．6.5h，6h D．6.5h，15h
【分析】直接利用众数和中位数的概念求解可得．
【解答】解：这组数据的众数为6h，中位数为第18个数据，即中位数为6h，
故选：A．
9．（4分）若二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），当t≤x≤2时，y有最大值3，最小值﹣1，则t的取值范围应是（　　）
A．﹣6≤t≤2 B．t≤﹣2 C．﹣6≤t≤﹣2 D．﹣2≤t≤2
【分析】根据二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），可以求得a的值，然后即可得到该函数的解析式，再根据二次函数的性质和当t≤x≤2时，y有最大值3，最小值﹣1，即可得到t的取值范围．
【解答】解：∵二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），
∴﹣1＝a×22﹣2+2，
解得a＝﹣，
∴y＝﹣x2﹣x+2＝﹣（x+2）2+3，
∴该函数的图象开口向下，对称轴是直线x＝﹣2，当x＝﹣2时，该函数取得最大值3，
∵当t≤x≤2时，y有最大值3，最小值﹣1，当x＝2时，y＝﹣1，
∴﹣6≤t≤﹣2，
故选：C．
10．（4分）将四张边长各不相同的正方形纸片①、②、③、④按如图方式放入矩形ABCD内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示，若已知阴影部分⑥与阴影部分⑤的周长之差，则不需测量就能知道周长的正方形的标号为（　　）

A．① B．② C．③ D．④
【分析】设①、②、③、④四个正方形的边长分别为a、b、c、d，用a、b、c、d表示出右下角、左上阴影部分的周长，利用整式的加减混合运算法则计算，得到答案．
【解答】解：设①、②、③、④四个正方形的边长分别为a、b、c、d，阴影部分⑥与阴影部分⑤的周长之差为l，
由题意得2（a+b﹣d+d）﹣2（b﹣a+a）＝l，
整理得2a＝l，
则知道l的值，不需测量就能知道正方形①的周长．
故选：A．
二、填空题（每小题5分，共30分）
11．（5分）中x的取值范围为　x≥﹣2　．
【分析】根据二次根式有意义的条件得到x+2≥0，然后解不等式即可，
【解答】解：根据题意得x+2≥0，解得x≥﹣2．
故答案为x≥﹣2．
12．（5分）当a＝　﹣1　时，的值为零．
【分析】根据分式的值为零的条件列式计算即可．
【解答】解：由题意得，a2﹣1＝0，a﹣1≠0，
解得，a＝﹣1，
故答案为：﹣1．
13．（5分）若一次函数y＝x+b（b为常数）的图象经过第一、三、四象限，写出一个符合条件的b的值为　﹣1（满足b＜0即可）　．
【分析】经过第一、三象限，说明x的系数大于0，得k＞0，又经过第四象限，说明常数项小于0，即b＜0，即可确定k的取值范围．
【解答】解：由题意得，k＝1＞0，b＜0
故符合条件的函数可以为：y＝x﹣1
故答案为：﹣1（满足b＜0即可）
14．（5分）已知x和y满足方程组，则代数式9x2﹣4y2的值为　6　．
【分析】由已知条件得到3x+2y＝4，3x﹣y＝1.5，再把9x2﹣4y2分解得到（3x+2y）（3x﹣2y），然后利用整体代入的方法计算．
【解答】解：由6x﹣4y＝3得3x﹣2y＝1.5，
9x2﹣4y2＝（3x+2y）（3x﹣2y）＝4×1.5＝6．
故答案为6．
15．（5分）如图，Rt△ACB中，∠C＝90°，AC＝BC＝6，点O在BC边上，且OB＝2，P是AB边上的动点，连接OP，以点O为圆心，OP长为半径为作⊙O．当⊙O与Rt△ACB的边相
切时，BP的长为　或6　．

【分析】当⊙P与AB相切，如图1，根据切线的性质得到∠OPB＝90°，则BP＝；当⊙P与AC相切，如图2，过P点作PH⊥BC于H，设OH＝x，则PH＝BH＝x+2，利用勾股定理得到x2+（x+2）2＝42，解得x＝﹣1，然后利用等腰直角三角形的性质得到PB的长．
【解答】解：∵∠C＝90°，AC＝BC＝6，
∴∠B＝45°，
当⊙P与AB相切，如图1，
∴OP⊥AB，
∴∠OPB＝90°，
∴BP＝OB＝；
当⊙O与AC相切，如图2，过P点作PH⊥BC于H，
则OP＝OC＝4，
设OH＝x，则PH＝BH＝x+2，
在Rt△POH中，x2+（x+2）2＝42，
解得x1＝+1（舍去），x2＝﹣1，
∴PH＝x+2＝+1，
∴PB＝PH＝+，
故答案为或+．


16．（5分）如图，矩形ABCD中，点A在函数y＝（k＞0，x＞0）的图象上，点B，C在x轴上，AD交y轴于点F，延长CD至点E，使CD＝3DE，连接BE交y轴于点P，连接PC，PA．若△PCB的面积为5，则k的值为　　，△POC的面积与△PFA的面积差为　　．

【分析】设DE＝a，AD与BE交于点Q，由题意可得CD＝3a，CE＝4a，根据四边形ABCD是矩形，可得AD∥BC，AB∥CD∥y轴，进而可得△EDQ∽△ECB，可得出＝，设DQ＝b，则BC＝4b，由△PCB的面积为5，可得出OP＝，再由OP∥CD，可得△BOP∽△BCE，可得到A（，3a），即可求得k，再三角形面积即可求得△POC的面积与△PFA的面积差．
【解答】解：如图，设DE＝a，AD与BE交于点Q，
∵CD＝3DE，
∴CD＝3a，
∴CE＝CD+DE＝4a，
∵四边形ABCD是矩形，
∴AD∥BC，AB∥CD∥y轴，AB＝CD，
∴△EDQ∽△ECB，
∴＝，即：＝，
∴＝，
设DQ＝b，则BC＝4b，
∴S△PCB＝BC•OP＝×4b•OP＝2b•OP，
∵△PCB的面积为5，
∴2b•OP＝5，
∴OP＝，
∵OP∥CD，
∴△BOP∽△BCE，
∴＝，
∴OB＝•OP＝•＝，
∴A（，3a），
∵点A在函数y＝（k＞0，x＞0）的图象上，
∴k＝×3a＝；
∵S△APB＝OB•AB＝×＝，
∴S△BOP+S△PFA＝﹣＝，
∴S△POC﹣S△PFA＝S△POC﹣S△PFA+S△BOP﹣S△BOP＝（S△POC+S△BOP）﹣（S△PFA+S△BOP）＝5﹣＝；
故答案为：；．

三、解答题（本大题有8小题，共80分）
17．（8分）（1）计算：（x+2）2﹣x（x﹣3）．
（2）解不等式：≥﹣2．
【分析】（1）根据完全平方公式以及单项式乘多项式的运算法则计算即可；
（2）根据解一元一次不等式的步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1，据此计算即可．
【解答】解：（1）（x+2）2﹣x（x﹣3）
＝x2+4x+4﹣x2+3x
＝7x+4；
（2）≥﹣2，
去分母，得3（2+x）≥2（2x﹣1）﹣12，
去括号，得6+3x≥4x﹣2﹣12，
移项，得3x﹣4x≥﹣2﹣12﹣6，
合并同类项，得﹣x≥﹣20，
系数化为1，得x≤20．
18．（8分）图1、图2是6×6的方格纸，点A，B都在格点上，按要求画图：

（1）请在图1中画一个五边形ABCDE，且是轴对称图形．
（2）请在图2中画一个六边形ABCDEF，且是中心对称图形．
【分析】（1）根据轴对称图形的性质画出图形即可．
（2）根据中心对称图形的性质作出图形即可．
【解答】解：（1）如图，五边形ABCDE即为所求作．
（2）如图，六边形ABCDEF即为所求作．

19．（8分）如图，小明想在自己家的窗口A处测量对面建筑物CD的高度，他首先测量出窗口A到地面的距离AB＝16m，又测得从A处看建筑物底部C的俯角为α＝30°，看建筑物顶部D的仰角为β＝45°，且AB，CD都与地面垂直，点A，B，C，D在同一平面内．
（1）求AB与CD之间的距离（结果保留根号）；
（2）求建筑物CD的高度（结果精确到0.1m）．（参考数据：≈1.41，≈1.73）

【分析】（1）作AE⊥CD于E，构建直角三角形，进而得出AE的长即可；
（2）根据等腰直角三角形的性质得出DE，CD的长解答即可．
【解答】解：（1）作AE⊥CD于E，

则四边形ABCE为矩形，
∴CE＝AB＝16，AE＝BC，
在Rt△ACE中，
tan∠CAE＝，
∴AE＝＝＝（m），
答：AB与CD之间的距离m；
（2）在Rt△ADE中，
∵∠DAE＝45°，
∴△ADE为等腰直角三角形，
∴DE＝AE＝AB＝m，
又∵CE＝AB＝16m，
∴CD＝CE+DE＝16+（m）≈43.7m，
答：建筑物CD的高度约为43.7m．
20．（10分）如图，二次函数y＝（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y＝kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．
（1）求二次函数的表达式及点B的坐标．
（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．

【分析】（1）将点A（﹣1，0）代入解析式求出m，求出点C坐标，根据点B与点C关于y轴对称求点B坐标．
（2）根据图象交点坐标求解．
【解答】解：（1）将（﹣1，0）代入y＝（x+2）2+m得0＝1+m，
解得m＝﹣1，
∴y＝（x+2）2﹣1，
当x＝0时，y＝3，
∴点C坐标为（0，3），
∵点B与点C关于轴对称，对称轴为直线x＝﹣2，
∴点B坐标为（﹣4，3）．
（2）∵点A坐标为（﹣1，0），点B坐标（﹣4，3），
由图象可知，（x+2）2+m≥kx+b时，x≤﹣4或x≥﹣1．
21．（10分）为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下尚不完整的统计图表．
调查结果统计表
组别
分组（单位：元）
人数
A
0≤x≤30
8
B
30＜x≤60
32
C
60＜x≤90
a
D
90＜x≤120
16
E
x＞120
4
请根据以上图表，解答下列问题：
（1）这次被调查的同学共有　100　人，a＝　40　，m＝　8　；
（2）求扇形统计图中C所在的扇形的圆心角度数；
（3）该校共有学生2000人，请估计每月零花钱的数额x在60＜x≤120范围内的人数．

【分析】（1）利用E组人数除以所占百分比可得被调查的总人数，然后再求出a和m的值即可；
（2）利用360°乘以C所占百分比可得C所在的扇形的圆心角度数；
（3）利用样本估计总体的方法可得答案．
【解答】解：（1）这次被调查的同学总数：4÷4%＝100（人），
a＝100﹣8﹣32﹣16﹣4＝40，
m%＝8÷100＝8%，
则m＝8，
故答案为：100；40；8；

（2）扇形统计图中C所在的扇形的圆心角度数是：360°×＝144°；

（3）每月零花钱的数新在60＜x≤120范围内的人数为（人），
答：每月零花钱的数额x在60＜x≤120范围内的人数为1120人．
22．（10分）某校学生食堂共有座位3600个，某天午餐时，食堂中学生人数y（人）与时间x（分钟）变化的函数关系图象如图中的折线OAB．
（1）试分别求出当0≤x≤20与20≤x≤38时，y与x的函数关系式；
（2）已知该校学生数有6000人，考虑到安全因素，学校决定对剩余2400名同学延时用餐，即等食堂空闲座位不少于2400个时，再通知剩余2400名同学用餐．请结合图象分析，这2400名学生至少要延时多少分钟？

【分析】（1）根据题意和函数图象中的数据，可以分别求得当0≤x≤20与20≤x≤38时，y与x的函数关系式；
（2）将y＝1200代入20≤x≤38对应的函数解析式中，即可得到这2400名学生至少要延时多少分钟．
【解答】解：（1）当0≤x≤20时，设y与x的函数关系式为y＝kx，
20k＝3600，得k＝180，
即当0≤x≤20时，y与x的函数关系式为y＝180x，
当20≤x≤38时，设y与x的函数关系式为y＝ax+b，
，得，
即当20≤x≤38时，y与x的函数关系式为y＝﹣200x+7600；
（2）∵空闲座位不少于2400个时，
∴有人坐的座位不大于1200个，
∵y＝﹣200x+7600，
∴当y＝1200时，﹣200x+7600＝1200，
解得，x＝32，
答：至少要延时32分钟．
23．（12分）【基础巩固】
（1）如图1，在四边形ABCD中，点P为AB上一点，∠DPC＝∠A＝∠B＝90°，求证：AD•BC＝AP•BP．
【尝试应用】
（2）如图2，在边长为4的菱形ABCD中，∠ABC＝60°，E为对角线BD上一点，且BE＝2DE，F为AD上一点，∠AEF＝30°，求AF的长．
【拓展提高】
（3）如图3，等边△DEF内接于矩形ABCD，其中点E，F分别在边AB，BC上，若BE＝4，CD＝5，求等边△DEF的边长．

【分析】（1）如图1，由∠DPC＝∠A＝∠B＝90°可得∠ADP＝∠BPC，即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题．
（2）如图2中，连接AC交BD于T．解直角三角形求出AE，再利用相似三角形的性质解决问题．
（3）如图3中，设DE＝EF＝DF＝x，利用勾股定理，利用方程求解即可．
【解答】（1）证明：如图1中，

∵∠A＝∠B＝∠DPC＝90°，
∴∠APD+∠BPC＝90°，
∵∠APD+∠ADP＝90°，
∴∠ADP＝∠BPC，
∴△ADP∽△BPC，
∴＝，
∴AD•BC＝AP•BP．

（2）解：如图2中，连接AC交BD于T．

∵四边形ABCD是菱形，∠ABC＝60°，
∴AB＝BC＝CD＝AD＝4，∠ABD＝∠DBC＝∠ADE＝30°，BD⊥AC，
∴AT＝AB＝2，BT＝TD＝2，
∵BE＝2DE，
∴BE＝，DE＝，ET＝，
∴AE＝＝＝，
∵∠AEF＝∠ADE＝30°，∠EAF＝∠DAE，
∴△AEF∽△ADE，
∴AE2＝AF•AD，
∴AF＝＝．

（3）如图3中，设DE＝EF＝DF＝x，

∵四边形ABCD是矩形，
∴∠A＝∠B＝∠C＝∠ADC＝90°，
∴BF＝，CF＝，
∴AD＝BC＝+，
∵AD2+AE2＝DE2，
∴（+）2+12＝x2，
解得x＝2或﹣2或0，
经检验，x＝2是方程的解，且符合题意，
∴等边△DEF的边长为2．
解法二：分别在CB、BC延长线上取M、N点，使得∠EMB＝∠DNC＝60°，可证：△EMF相似于△FND，设BF＝x，可列方程求解．
24．（14分）定义：有一组对角互余的凸四边形称为对余四边形．
（1）如图1，在11×7的网格中，点A，B，D都是网格的格点，请你确定所有格点C，使得四边形ABCD是对余四边形．
（2）如图2，EF是⊙O的直径，点A，D，C在⊙O上，AF，CE相交于点B．求证：四边形ABCD是对余四边形．
（3）已知四边形ABCD是对余四边形．
①如图3，若DA＝DB，BC＝2，CD＝4，AC＝6，求∠DAB的度数；
②在平面直角坐标系中，设点A（﹣1，0），B（3，0），C（1，2），求线段DO长度的取值范围．
【分析】（1）利用对余四边形的定义，找出使∠A+∠DCB＝90°的点C即可；
（2）根据圆周角的度数等于它所对的弧的度数的一半，通过计算证明∠A+∠C＝90°，然后利用对余四边形的定义得出结论即可；
（3）①构造等腰三角形△DCK，使DK＝DC，∠CDK＝∠ADB，得到△ADC≌△BDK，BK＝AC；利用勾股定理求得CK，再利用勾股定理的逆定理，得出∠KDC＝90°，从而∠ADB＝90°，△ADB为等腰直角三角形，结论可求；
②通过计算可得∠ABC＝45°，由对余四边形的定义可得∠ADC＝45°，可知点D在优弧上运动，利用圆周角定理可得∠AMC＝90°，则⊙M的半径可求，当OD经过圆心时最大，OD的值最大，当D点与电脑A重合时OD最小，但不能组成四边形，由此，OD的取值范围可得．
【解答】解：（1）由对余四边形的定义，点C满足∠A+∠DCB＝90°，
如图1所示，点C1，C2，C3即为所求的点；

（2）证明：∵EF是⊙O的直径，
∴为半圆，即的度数为180°．
∵圆周角的度数等于它所对的弧的度数的一半，
∴∠A的度数＝的度数，∠C的度数＝的度数．
∴∠A+∠C＝的度数+的度数＝度数＝＝90°．
∴四边形ABCD是对余四边形．
（3）①如图3，以DC为腰作等腰三角形DCK，使DK＝DC，∠CDK＝∠ADB，

则∠ADB+∠BDC＝∠CDK+∠BDC．
∴∠ADC＝∠BDK．
∵DK＝DC，
∴∠DKC＝∠DCK＝．
∵DA＝DB，
∴∠DAB＝∠DBA＝．
∴∠DAB＝∠DCK．
在△ADC和△BDK中，
．
∴△ADC≌△BDK（SAS）．
∴AC＝BK＝6．
∵四边形ABCD是对余四边形，且由题意∠ADC+∠ABC＞90°，
∴∠DAB+∠DCB＝90°．
∴∠DCK+∠DCB＝90°．
即∠KCB＝90°．
∴CK＝．
∵DK＝DC＝4，
∴DK2+CD2＝32．
∵CK2＝32，
∴DK2+CD2＝CK2．
∴∠KDC＝90°．
∴∠ADB＝∠KDC＝90°．
∴∠DAB＝∠DBA＝＝45°．
②如下图，过C作CE⊥x轴于E，

∵点A（﹣1，0），B（3，0），C（1，2），
∴OA＝1，OE＝1，OB＝3，CE＝2．
∴BE＝OB﹣OE＝2，AE＝OA+OE＝2．
∴BE＝CE，
∵CE⊥BE，
∴∠ABC＝∠ECB＝45°．
∵四边形ABCD是对余四边形，
∴∠ADC+∠ABC＝90°．
∴∠ADC＝45°．
∴点D在以AC为弦，对AC张开的角度为45°的优弧上运动．
设这条弧所在圆的圆心为M，连接MA，MC，则∠AMC＝2∠ADC＝90°．
∵MA＝MC，
∴∠MAC＝∠MCA＝45°．
∵CE＝AE＝2，CE⊥AB，
∴∠EAC＝∠ECA＝45°，
∴∠MAE＝90°．
∴四边形MAEC为正方形．
∴MA＝2．
∴OM＝．
∵当OD经过圆心M时最大，OD的值最大，此时OD＝MD+MO＝2+，
当点D与点A重合时，OD最小，OD＝OA＝1，但此时不能组成四边形，
∴OD的取值范围为1＜OD≤2+．