





初中数学人教版九年级上册24.4 弧长及扇形的面积获奖课件ppt
展开【2019·长沙】一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A.2π B.4π C.12π D.24π
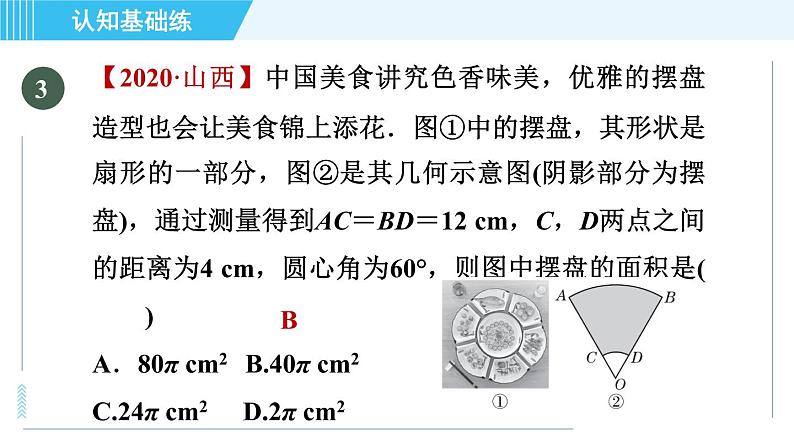
【2020·山西】中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12 cm,C,D两点之间的距离为4 cm,圆心角为60°,则图中摆盘的面积是( )A.80π cm2 B.40π cm2C.24π cm2 D.2π cm2
【点拨】连接CD,首先证明△OCD是等边三角形,求出OC=OD=CD=4 cm,再根据S阴影=S扇形OAB-S扇形OCD求解即可.
A.π-1 B.π-2C.π-3 D.4-π
(1)求证:CE是⊙O的切线;
证明:如图,连接BF,OC,∵AB是⊙O的直径,∴∠AFB=90°,即BF⊥AD.∵CE⊥AD,∴BF∥CE.∵点C为劣弧BF的中点,∴OC⊥BF.∵BF∥CE,∴OC⊥CE.∵OC是⊙O的半径,∴CE是⊙O的切线.
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
【点拨】计算不规则图形的面积时,常常通过割补法将不规则图形的面积转化为几个规则图形面积的和或差的形式.
解:如图,连接OF,与AC交于点M,∵OA=OC,∠BAC=30°,∴∠BAC=∠ACO=30°.∴∠BOC=60°.由(1)知OC⊥CE.又∵AD⊥CE,∴AD∥OC.∴∠FAM=∠OCM=30°.∴∠FAB=60°.又∵OA=OF,∴△AFO为等边三角形.∴AF=OF=OC.
【点拨】本题运用了作差法,通过作辅助线,将阴影部分的面积转化为△ACD与扇形COE的面积之差求解.
初中数学人教版九年级上册24.4 弧长和扇形面积作业课件ppt: 这是一份初中数学人教版九年级上册24.4 弧长和扇形面积作业课件ppt,共19页。
初中数学人教版九年级上册24.4 弧长及扇形的面积精品课件ppt: 这是一份初中数学人教版九年级上册24.4 弧长及扇形的面积精品课件ppt,文件包含人教版初中数学九年级上册2441弧长和扇形面积课件PPTpptx、人教版初中数学九年级上册2441弧长和扇形面积分层练习docx、人教版初中数学九年级上册2441弧长和扇形面积教案docx、人教版初中数学九年级上册2441弧长和扇形面积预习案docx等4份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
数学人教版第二十四章 圆24.4 弧长及扇形的面积教案配套ppt课件: 这是一份数学人教版第二十四章 圆24.4 弧长及扇形的面积教案配套ppt课件,共43页。PPT课件主要包含了C2πr,Sπr2,创设情境,弧长公式,牛刀小试,精讲点拨,SπR2,扇形面积公式,尝试练习2,没有最好只有更好等内容,欢迎下载使用。













